Eta? :D

Eta? :D Jack: Eta? : D

25 gru 18:49

Jack: x⁴ − 7x² − 4x + 22 wyznacz najmniejsza wartosc funkcji... (bez uzywania pochodnej)

25 gru 18:50

Eta: y_min=2 dla x= 2

25 gru 19:01

Jack: jakies rozpisanie ? bo z pochodnej tez by mi tak wyszlo, ale ... z odpowiednim pogrupowaniem? emotka

25 gru 19:01

Eta: f(x)= (x²−4)²+(x−2)²+2 y_min= f(2)= 2

25 gru 19:08

Jack: wolfram pokazuje (x−2)⁴ + 8(x−2)³ + 17(x−2)² + 2 ale to chyba nie mozliwe dla normalnego czlowieka ; D

25 gru 19:08

Jack: o kurcze, nie wpadlbym na to...

25 gru 19:09

Jack: o skad pomysl na akurat takie cos : D

25 gru 19:10

Jack: i tak wlasciwie skad wiemy ze to jest minimalne...jak to odczytac jesli mam takie rownanie

25 gru 19:11

Jack: tak duzo pytan...tak malo odpowiedzi

25 gru 19:21

tx: f(x)= (x²−4)²+(x−2)²+2 (x²−4)²≥0 (x−2)²≥0 f(x)≥2

25 gru 19:32

Eta: a²+b²+2≥0 dla a=b=0 najmniejsza wartość jest równa 2 zatem ..............

25 gru 19:33

Jack: aaa... no dobra

25 gru 19:33

Eta:

25 gru 19:34

Jack: a skad pomysl z pogrupowaniem w akurat taki sposob? : D jest na to jakis poradnik moze...

25 gru 19:34

Eta: Trening, trening emotka

Na maturze może być takie zadanie: Wykaż ,że dla x∊R zachodzi nierówność x⁴−7x²−4x+22≥0 .................

25 gru 19:37

Jack: omijam i ide do nastepnego. : D

25 gru 19:38

Eta:

25 gru 19:38

Eta: zad1/ (7pkt Rozpatrujemy wszystkie trójkąty ostrokątne równoramienne wpisane w okrąg o promieniu r=2. Wyznacz długość wysokości tego z rozpatrywanych trójkątów , którego pole jest największe oraz oblicz to pole. Powodzenia emotka

25 gru 19:43

Eta: zad2/ (4pkt W trapezie ABCD o podstawach AB i CD, dwusieczna kąta ostrego przy wierzchołku B jest prostopadła do ramienia AD i dzieli je w stosunku 3:2, licząc od wierzchołka A. Oblicz stosunek pól figur, na które ta dwusieczna podzieliła trapez ABCD Na dzisiaj .... wystarczy emotka

25 gru 19:48

Jack:

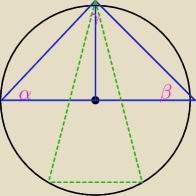
α , β , γ < 90 stopni...

	a * h
P =
	2

Pole maxymalne bedzie jesli...hmm

	1
Pole zrobmy za pomoca a * b * sin α *		, wtedy pole najwieksze przy najwiekszym kacie....
	2

zalozmy ze kat γ bedzie najwiekszy ...wtedy bylby polozony na srednicy okregu skoro bylby polozony na srednicy, to mialby 90 stopni...czyli nie spelnia warunku ostrokatnego wiec musi byc polozony delikatnie wyzej, albo nizej... hmmm tyle opcji

25 gru 19:54

Kacper: Zabieram zadanka emotka

25 gru 20:14

Jack:

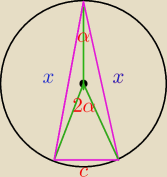
c² = r² + r² − 2 r² cos 2 alfa c² = 8 − 8 cos 2 alfa c² = 8(1−cos 2 alfa) oraz c² = 2x² − 2x² cos alfa c² = 2x² (1 − cos alfa) 8(1− cos²α + sin²α) = 2x² (1 − cos alfa) 8(2 sin²α) = 2x²(1−cos α)

25 gru 20:19

Eta: Hej Kacper emotka

Jak to? zabierasz? emotka

25 gru 20:28

Jack:

	a² √3
P =
	4

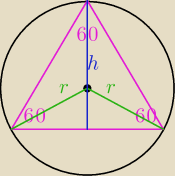
	2
r =		h (z wlasnosci trojkata rownobocznego wpisanego w okrag)
	3

2
	h = 2
3

	a √3
h = 3 =
	2

a = 2 √3 P = 3√3 hmmm... a tu chyba powinienem z pochodnej obliczyc...cos za latwo...

25 gru 20:36

Eta: Skąd wiesz,że trójkąt równoboczny Masz to wykazać ,że taki właśnie jest !

25 gru 20:41

Kacper: W dzisiejszych czasach mamy Eta geniuszy...

Oni mówią, że tak jest i tak myślą, ale uzasadnić tego nie potrafią

Moi uczniowie tak zazwyczaj robią

25 gru 20:43

Eta: I dostaną za takie zad. na maturze 0 pkt i będzie

25 gru 20:44

Jack: najwieksze pole ma koło, a kazda figura foremna dazy do kola, wiec jakakolwiek figura wpisana w okrag to ma najwieksze pole jesli jest foremna...

25 gru 20:45

Jack: aczkolwiek za chiny bym tego nie umial wykazac...

25 gru 20:46

Eta: 0pkt emotka

25 gru 20:48

Jack: no jak, wszystko sie zgadza...

25 gru 20:51

Jack: CI co sprawdzaja sa oszukistami ! emotka

foch

25 gru 20:52

Eta: Zamiast 7pkt ............. 0pkt Rozwiązuj następne ( może też będzie 0pkt ?

25 gru 20:53

Jack: nie ma bata...zrobie to zadanie

25 gru 21:02

Jack: 14 % nie strace na byle zadaniu !

25 gru 21:04

Eta: No wreszcie logiczne myślenie emotka

25 gru 21:05

Jack:

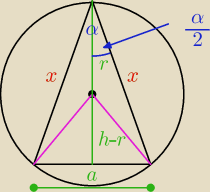
	1		1
P_Δ =		* a * h =		* x² * sin α
	2		2

a h = x² sin α

	a h
x² =
	sin α

tw. pitagorasa...

	a
h² = x² − (		)²
	2

	a h		a²
h² =		−
	sin α		4

	α		α
sin α = 2sin		cos
	2		2

	a		a
sin		=
	2		2x

	a		h
cos		=
	2		x

	a h
sin α =
	x²

h² = no super...wrocilem do poczatku : D

25 gru 21:54

Eta:

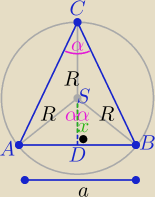
Podpowiem:

	a*h
P=		, α∊(0^o,90^o) −− z treści zadania
	2

a= 2Rsinα i h=R+x i x= Rcosα ⇒ h=R(1+cosα) P(α)=...... P^'(α)=..... ................... α= 60^o ........... Odp: h=3, a= 2√3 , P=3√3

25 gru 22:10

Jack: Wszystko co wyzej napisalem jest bez sensu, ale to co nizej jest GIT

: z tw. pitagorasa

	a
(h−2)² = r² − (		)²
	2

a² = 16h − 4h²

	1
P =		* h * √16h − 4h² =
	2

	1
=		* h * √4(4h − h² =
	2

= h √4h − h² = = √4h³ − h⁴ pochodna

DDDDDDDD P ' (h) = U{1}{2√4h³−h⁴ * (12 h² − 4h³) przyrownuje do zera i mam ... 12 h² − 4h³ = 0 h²(12 − 4h) = 0 h = 0 <−−nie nalezy do dziedziny (h>0) lub 4h = 12 h = 3 wtedy p max wynosi : Pmax(3) = √4*27 − 81 = √27 = √9*3 = 3√3 WYSZŁO

HAHAHAHAH

25 gru 22:13

Jack: a widzisz, nawet nie zauwazylem twojego postu, ale sam to wymyslilem...jestem genialny ^^

25 gru 22:15

Kacper: Wmawiaj sobie

25 gru 22:16

Jack: no tak... apropo, jak sie tu zapisuje w potędze ułamek np. x do potegi jedna druga...

	1
x/div>
	2

bo cos sie nie da...

25 gru 22:17

Eta:

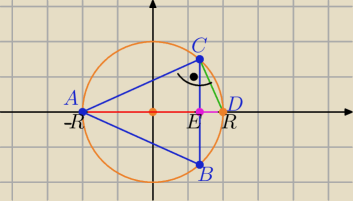2 sposób ( bez trygonometrii) ( analitycznie)

	a
\|CE\|=		, \|AE\|=h i \|AD\|=2R i \|ED\|=x i h∊(0,2R)
	2

|CE|²=|AE|*|ED| ⇒................... a=2√h(2R−h) P(h)= h*√h(2R−h) P^'(h)=................ h=................. P=............

25 gru 22:21

Eta: x^¹₂

25 gru 22:22

Jack: ee...to trza znac twierdzenie o cięciwach...że |CE|² = |AE| * |ED|

25 gru 22:23

Jack: no, jak to zrobic : D

25 gru 22:24

Jack: ten drugi sposob jest prawie taki jak moj, w sensie z tego samego wzoru pole i wlasciwie wiekszosc ta sama

25 gru 22:25

Eta: "genialny" emotka

i tego nie potrafi? https://matematykaszkolna.pl/forum/przyklady9.html

25 gru 22:25

Jack: aaaa

	1
x
	2

x^¹₂

25 gru 22:26

bezendu: x^1/2

25 gru 22:26

Eta: x^0,5 emotka

25 gru 22:27

bezendu: emotka

25 gru 22:28

Eta: Hej bezendu łap ....... emotka

25 gru 22:28

Benny: Skąd Ty Eta takie ładne zadanka bierzesz? emotka

25 gru 22:29

bezendu: Pomyśleliśmy o tym samym

Dziś biorę oba emotka

25 gru 22:29

Eta: x^{x^x}

25 gru 22:29

Jack:

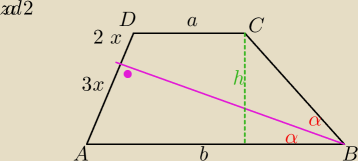
25 gru 22:32

Eta: X^{x^{x^{x^x}}}

25 gru 22:33

Eta: Rysunek bardzo ładny emotka

Jeszcze tylko do tego podaj poprawne rozwiązanie ( za całe 4pkt emotka

25 gru 22:34

Jack:

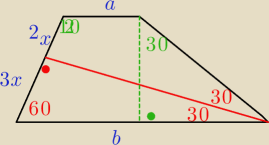
3 α = 90, wiec α = 30 stopni no i fajno

25 gru 22:36

Jack: NIEEEEEEEEEEEE co ja gadam on nie jest rownoramienny WRÓĆ

25 gru 22:36

Eta:

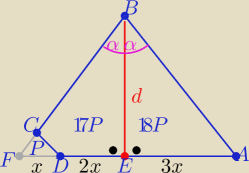
Ja bym taki rys. narysowała emotka

I wszystko jasne...... dodać tylko komentarze i Odp: ..........

25 gru 22:58

Jack:

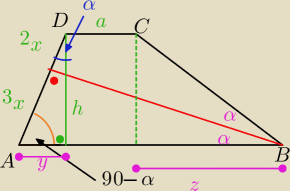
	1
P_C = P _T_R_A_P_E_Z_U =		* (a+b) * h
	2

	h
cos α =		=>> h = 5x * cos α
	5x

	1
P_Δ = Pole _T_R_Ó_J_K_Ą_T_A =		* 3x * b * cos α
	2

	1
P_C − P_Δ =		x cosα (5a+2b) = Pole _T_E_G_O _C_Z_E_G_O_Ś
	2

Pole _T_E_G_O _C_Z_E_G_O_Ś		5a + 2b
	=
P_Δ		3b

ale nie mam a, wiec wprowadzam sobie 3 zmienne nowe

	y
tg α =
	h

	3x
sin α =
	a + y + z

	h
tg 2 α =
	z

Po podstawieniu wychodzi taki bałagan, że matko jedyna...muszę wynaleźć inny sposób na wyznaczenie a

25 gru 23:16

Eta:

25 gru 23:19

Jack: @Eta Ty tylko byś dorysowywała jakieś bajery...byleby było coś więcej jak w poleceniu : D

25 gru 23:19

Eta: Jak Ty napiszesz tę maturę ? emotka

25 gru 23:21

Jack: mam nadzieje ze nie bedzie takich chinskich zadan...ciagle jakas planimetria, nie mozna dac czegos normalnego!?

25 gru 23:21

Jack: czemu tam jest 18P a w tym drugim 17 P ? skad takie dane...

25 gru 23:23

Eta:

Dać jeszcze jedno ?....... z planimetrii emotka

25 gru 23:23

Eta: Z podobieństwa trójkątów ABF i CDF z cechy (kkk) ! w skali k= 6

	P(ABF)
to		= k²=....
	P(CDF)

itd...... .................

25 gru 23:26

Jack: no tak , ale skad wiesz ze np. P = 18 znasz tylko to, ze jest 3x i 2x skad wiesz inne dane zeby wyznaczyc pole

	1
P =		* a * h...
	2

25 gru 23:28

Jack:

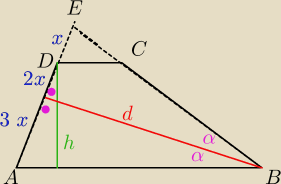
Twoj rysunek, tylko wg mnie

25 gru 23:28

Eta: Widzisz trójkąty prostokątne przystające ? o polach ....

25 gru 23:29

Eta: ΔABF ≡ ΔBFE

25 gru 23:30

Jack: Rozważmy trapez prostokątny ABCD o podstawach AB oraz CD ? Nie dziękuję ! xd moglabys przypomniec ile wynosi cos 4x (cosinus) ? cos (2x+2x) = cos2x * cos 2x − sin 2x * sin 2x = = (cos² x − sin²x)² − 4 sin²x cos²x = cos⁴ x − 2 sin²xcos²x + sin⁴x − 4 sin²x cos²x = = cos⁴ x + sin⁴x − 6 sin²x cos²x da sie to jakos jeszcze... uproscic

25 gru 23:34

Jack: no wlasnie za chiny nie moge tego zrozumiec... jak mozna miec 2 niewiadome we wzorze i otrzymac wynik 18 no ja nie rozumiem jeszcze takich rzeczy

25 gru 23:35

Eta: cos(4x)=8cos⁴(x)−8cos²(x)+1

25 gru 23:36

zombi: cos⁴x+sin⁴x = (sin²x+cos²x)² − 2sin²xcos²x = 1 − 2sin²xcos²x

25 gru 23:36

Jack: dobra, dzieki wam

25 gru 23:37

Eta: cos(4x)= 2cos²(2x)−1= 2[(2cos²x−1)²−1] =............ patrz wyżej .. emotka

25 gru 23:39

Jack: czyli inaczej cos(4x) = 1 − 8 sin²x cos²x Czyli jakbym mial zadanko cos4x + 2cos²x = 1 i x ∊ <0;π> no to 1 − 8 sin²x cos²x + 2cos²x = 1 1 − 8 cos²x(1−cos²x) + 2cos²x = 1 1 − 8 cos²x + 8 cos⁴x + 2cos²x = 1 8 cos⁴x + − 6 cos²x = 0 2cos²x(4cos²x − 3) = 0 i dalej to wiadomo

25 gru 23:45

Jack: no dobra, to dzieki za pomoc...ja taki kompletny nieogar ale co zrobisz jak nic nie zrobisz... @Eta −> jutro te zadanko z planimetrii ...aczkolwiek inne bylyby lepsze : D

25 gru 23:46

Jack: to dobranoc wszystkim i jeszcze raz zdrowych, spokojnych swiat

25 gru 23:46

Eta: Proponuję takie rozwiązanie tego równania: cos(4x)+2cos²x=1 , x∊<0,π> i 2cos²x−1= cos(2x) zatem: cos(4x)= −cos(2x) ⇒ 4x= −2x+2kπ lub 4x= 2x+2kπ

	π
x= k*		lub x= kπ , k∊C
	3

Odp:..... podaj już sam Dobranoc emotka

26 gru 00:02

Eta: Poprawiam ( bo nie zauważyłam minusa po prawej stronie) sorry za błędny zapis cos(4x)= −cos(2x) ⇔ cos(4x)= cos(π−2x) 4x= π−2x+2kπ lub 4x= −π+2x+2kπ 6x= π+2kπ lub 2x= −π+2kπ

	π		π		π
x=		+k*		lub x=		+kπ , k∊C
	6		3		2

dla x∊<0,π> Odp: ....... 2sposób cos(4x)+cos(2x)=0 ⇔ 2cos(3x)*cos(x)=0 cos(3x)=0 lub cos(x)=0

	π		π
3x=		+kπ lub x=		+kπ
	2		2

	π		π		π
x=		+k*		lub x=		+kπ , k∊C
	6		3		2

dla x∊<0, π> Odp:......................

26 gru 10:41

Saizou : lub też cos(4x)+cos(2x)=cos²(2x)−sin²(2x)+cos(2x)=cos²(2x)−(1−cos²(2x))+cos(2x)= 2cos²(2x)+cos(2x)−1=0 Δ=1+8=9

	−1−3		−4		−1+3		1
cos2x=		=		=−1 lub cos(2x)=		=
	4		4		4		2

26 gru 10:51

Eta:

26 gru 11:05

Metis: Zazdroszczę takiej geometrycznej wyobraźni, którą władasz Eta emotka

26 gru 11:35

Eta:

26 gru 11:37

Jack: Sześcian o krawędzi 6 przecięto płaszczyzną przechodzącą przez przekątną podstawy tworzącą z podstawą kąt α. Oblicz pole otrzymanego przekroju, jeśli α = 60 stopni.

26 gru 11:39

Jack:

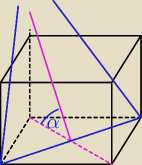
czy by tak to wygladalo ?

26 gru 11:45

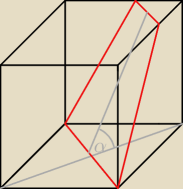
Saizou : rysunek

masz rysunek i kombinuj

26 gru 11:47

Jack: czyli dobrze narysowalem...jej : D

26 gru 11:47

Eta:

26 gru 11:49

Saizou : a dlaczego tworzy się trapez a nie np. trójkąt? i pytanie dla jakich α byłby to trójkąt? emotka

26 gru 11:49

Jack: zadanie podobne do tego : https://matematykaszkolna.pl/forum/310501.html tylko nie wiemy gdzie plaszczyzna przecina krawedzie gornej podstawy...

26 gru 11:50

Jack: skoro szescian to strzelam ze do 45 stopni bylby trojkat

26 gru 11:51

Metis: Strzelaj tak dalej emotka

W matematyce nie ma strzałów.

26 gru 11:52

Saizou : nie ma strzałów, zrób jaką analizę emotka

na rysunku gdzie by się tworzył trójkąt ?

26 gru 11:53

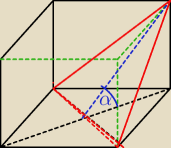
Jack:

26 gru 11:56

Saizou : no i dalej emotka

jak można wyliczyć ten kąt emotka

26 gru 12:03

Jack:

	a
tg alfa =		= √2
	^{a √2}₂

α ≈ 54 stopnie

26 gru 12:08

Saizou : emotka

czyli α z jakiego może być zakresu żeby dostać trójkąt ?

26 gru 12:09

Jack: no dobra, wiadomo ze musi byc trapez wiec wrocmy do zadania : D

26 gru 12:09

Saizou : jakieś pomysły na zadanie ? emotka

26 gru 12:10

Jack: gdybym mial, bym nie pytal ^^ no nie wiem gdzie moze byc polozony...w sensie gorna podstawa wiec wprowadzic kilka niewiadomych? ...

26 gru 12:13

Saizou : czy można obliczyć jakoś wysokość tego trapezu ?

26 gru 12:13

Jack: to jest zmienna jak kazda inna... mozna jedynie uzaleznic od czegos

26 gru 12:15

Saizou : pomyśl nad sinusem kąta 60^o oraz wysokości sześcianu

26 gru 12:16

Kacper: Saizou widzisz jak to łatwo tłumaczyć komuś

26 gru 12:28

Saizou : easy work Kacper

(oczywiście żart)

26 gru 12:32

Jack:

	H
sin 60 =
	h

	√3
H = h *
	2

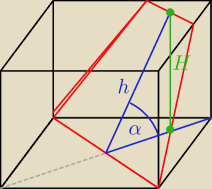
26 gru 12:36

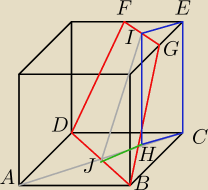
Saizou : rysunek

	IH		6		√3
sinα=		=		=		→\|IJ\|=4√3
	IJ		IJ		2

z tw. Pitagorasa mamy (4√3)²=|JH|²+6² |JH|²=16*3−36=58−36=12→|JH|=2√3, zatem |CH|=3√2−2√3=EI ΔEFG~ΔBCD

CJ		EI
	=
DB		FG

3√2		3√2−2√3
	=
6√2		FG

|FG|=2(3√2−2√3)

	1
P=		(6√2+6√2−4√3)*4√3=2√3(12√2−4√3)=8√3(3√2−√3)=
	2

24√6−24=24(√6−1)

26 gru 12:40

Eta: "niepokorny Jacuś" emotka

26 gru 12:41

Jack: No, dziękować, nie można tak od razu

z moich obliczeń wyszło, że h = 4√3, a = 6√2

	1
do wzoru P =		* (a+b) * h brakowało mi tylko "a"
	2

26 gru 12:42

Jack: jestem tak skromny ze nie pisalem, nawet jesli cos wiedzialem : )

26 gru 12:43

Saizou : ale skąd my mamy wiedzieć że nie chcesz gotowca

choć nie powiem sam często podaję gotowce jak mi się nie chce tłumaczyć

26 gru 12:44

Eta:

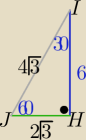
@Saizou Czemu nie tak: |JI|=4√3 i |JH|=2√3

26 gru 12:46

Saizou : Etuś jakoś wolę funkcje trygonometryczne niż własność kątów w trójkącie 30,60,90

26 gru 12:48

Eta:

26 gru 12:48

Kacper: Co kto lubi emotka

Ja lubię schabowe

26 gru 12:51

Eta:

26 gru 12:51

Jack: też wole użyć funkcji tryg. jak Saizou, bo ten trojkat 30 60 90 zawsze mi cos namiesza : D

26 gru 12:52

Eta:

26 gru 12:52

Saizou : ważne żeby nie mylić się w obliczeniach i dobrze rozumować emotka

26 gru 12:53

Eta: Wtedy odp masz w 1 sek emotka

i nie musisz prosić Pitagorasa o pomoc

26 gru 12:53

Saizou : oj tam 5 sek. to nie jakiś ogrom czasu

równie dobrze mogę policzyć tg60 emotka

26 gru 12:54

Eta: No to następne zadanko emotka

za (3pkt Rozważmy trapez prostokątny ABCD o podstawach AB i CD oraz katach prostych przy wierzchołkach A i D. Wiedząc,że punkt S jest środkiem okręgu wpisanego w ten trapez oraz |SB|=4 i |SC|=2 Oblicz obwód trapezu ABCD emotka

26 gru 12:58

Eta: A teraz idę na spacer z

26 gru 13:05

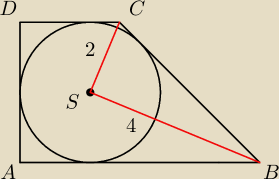
Kacper: rysunek

To akurat "znane" zadanko emotka

26 gru 13:05

Jack: to za chwile, wpierw musze sprawdzic znaczy "najpierw" musze sprawdzic czy Saizou nie zrobil jakiegos bledu w liczeniu ^^

26 gru 13:06

Eta: @Kacper To zadanko z wsip z listopada 2015 ( rozszerzenie) emotka

26 gru 13:08

Jack: tak, tak, wszyscy to wiemy Eta

26 gru 13:09

Eta: Coś TY? nie wierzę

26 gru 13:10

Jack:

	1
P =		r * Obwód
	2

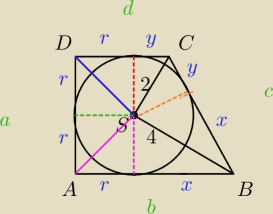
Obwód = a + b + c +d a + c = b + d (z wlasnosci okregu wpisanego w czworokat) a = 2 r b = r+ x c = x+y d = r + y 2r + x + y = 2r + x + y...

pitagoras : 16 = x² + r² oraz 4 = y² + r² x² − y² = 12

26 gru 13:32

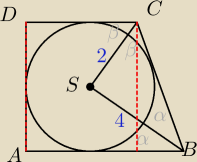
Saizou : rysunek

2α+2β=180 α+β=90, zatem kąt BSC=90 , stąd BC=2√5

	AD
sin2α=
	2√5

	AD
2sinαcosα=
	2√5

4√5sinαcosα=AD

	2		1
sinα=		=
	2√5		√5

	4		2
cosα=		=
	2√5		√5

	1		2		8√5
AD=4√5*		*		=
	√5		√5		5

	8√5		8√5+10√5		36√5
Ob=2(AD+BC)=2(		+2√5)=2*		=
	5		5		5

26 gru 13:41

Jack: aaa...z katow to trza bylo : D

26 gru 13:46

Kacper: Saizou przekombinował emotka

26 gru 13:50

Saizou : Kacper to była pierwsza myśl

26 gru 13:51

Kacper: Lepiej poczekać na drugą myśl dzięki której szybciej się liczy

26 gru 13:53

Saizou : szczerze nie zajęło mi to więcej niz 30 s

dłużej to wklepywałem do komputera

26 gru 13:54

Jack:

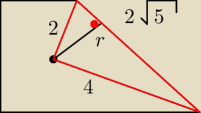
wystarczy wiedza ze tam jest kat prosty... wtedy Pole tego tam trójkąta

	1
P =		* 2√5 * r
	2

oraz

	1
P =		* 2 *4
	2

P = P 2√5 * r = 8

	4√5
r =
	5

wtedy

	18√5		36√5
Obwód = 2 (2*r + 2√5) = 2 (		) =
	5		5

26 gru 14:04

Kacper: Dobrze, to ja napiszę bez sinusów i wzorów, których "przeciętny" uczeń nie pamięta. |BC|=2√5 (wiadomo dlaczego)

	2P		8		4√5
r=		⇒ r=		=
	\|BC\|		2√5		5

	8√5
Zatem L=2(\|AD\|+\|BC\|)=2(		+2√5)=...
	5

I po co... się męczyć emotka

26 gru 14:10

Kacper: Coś odświeżanie nie działa... emotka

26 gru 14:11

Jack: akurat wzory ktorych uzyl Saizou to sa w tablicach maturalnych...

26 gru 14:12

Kacper: To, że są, to nie znaczy, że ktoś je potrafi wykorzystać. Jest bardzo dużo wzorów, ale jakoś średnia wyników matury rozszerzonej to około 40%.

26 gru 14:17

Jack: bo na rozszerzeniu dawaja takie rzeczy, ze te wzory sie nie przydaja : D

26 gru 14:18

Kacper: Owszem, że się przydają, tylko trzeba nauczyć się je wykorzystywać emotka

26 gru 14:19

Saizou : przydają się, tylko trzeba troszkę pomyśleć xd

26 gru 14:19

Jack: troszkę, to czasami za dużo : D

26 gru 14:20

Kacper: To teraz zadanko ode mnie emotka

− będzie proste emotka

Wyznacz najmniejszą wartość funkcji określonej wzorem: f(x)=log_1/2(−|x−1|−|4−x²|) dla x>0.

26 gru 14:25

Jack: pochodna logarytmu? : D

26 gru 14:26

Kacper: Małe błędy w treści emotka

Funkcja jest taka: f(x)=log₍1/2) (|x−1|−|4−x²|) Nie ma mowy o dziedzinie emotka

26 gru 14:27

Kacper: I jeszcze jedno: tym razem nierówności emotka

Uzasadnij, że dla dowolnych liczb a i b prawdziwa jest nierówność: 5a²+8ab+5b²>−4

26 gru 14:30

Kacper: O i jeszcze bardzo fajne mam zadanko z ciągów emotka

Dany jest ciąg określony wzorem a_n=2+3+3²+...+3ⁿ.

	4a_n
Liczba g jest równa lim_{n →∞}		.
	a_n+1

Zakoduj trzy pierwsze cyfry rozwinięcia dziesiętnego liczby g.

26 gru 14:39

Benny: @Kacper myślałem, że coś trzeba będzie przekształcić ładnie tą nierówność, a tu nawet nie ma co

26 gru 15:13

Eta: (2a+2b)²+a²+b²+4>0

26 gru 15:16

Jack: e no...nawet nie daliscie mi sprobowac : D

26 gru 15:23

Eta: Pisałeś wczoraj,że takie zadanie .......... "omijam i idę dalej" emotka

26 gru 15:25

Jack: Prosze nie wklejac rozwiazania do tej granicy...to chetnie oblicze ; D

26 gru 15:25

Eta: A już miałam "wklejać"

26 gru 15:26

Jack: ale udowadnianie z a i b to jedna z moich ulubionych rzeczy... lubie sie w to pobawic : D

26 gru 15:26

Jack: zamiast lim n→∞ bede pisac tylko lim, coby latwiej sie pisalo : D lim U{4*(0,5+ ³₂*3ⁿ}{ chociaz wlasciwie nie musze liczyc tej sumy...heheh jestem genialny.

	4 a_n		4
lim		=		...hmm
	a_n * q		3

26 gru 15:36

Jack: to nie moze byc takie proste

26 gru 15:38

Jack: ha, wiedzialem, ze cos skopalem...jeszcze ta dwójka coś robi

26 gru 15:39

Jack: nie, wlasciwie to chyba nic...

26 gru 15:41

Jack: jednak robi !...hmm

26 gru 15:56

Jack:

lim

=

 2 
3n(6 + 
)
 3n 

= lim 

=

 9 1 
3n(
 + 
)
 2 2*3n 

6

12

4

=

=

=

9 
2 

9

3

LOL

26 gru 16:23

Jack: jaki jest poprawny wynik?

26 gru 16:24

Jack: halo? :x

26 gru 16:45

Kacper: 0 pkt

26 gru 16:48

Metis:

	4a_n
lim_n−>∞
	a_n+1

a_n=2+3+3²+...+3ⁿ Licznik: 4(2+3+3²+...+3ⁿ) = 8+4*3+4*3²+...+4*3ⁿ Mianownik: 2+3+3²+...+3ⁿ⁺¹ = 2+3+3²+...+3ⁿ⁺¹ I teraz sumę licznika / mianownika − ciąg geometryczny Będzie emotka

26 gru 16:56

Kacper: 0 pkt

26 gru 16:56

Metis: Ale tok myslenia dobry czy skopałem licznik/ mianownik ?

26 gru 16:57

Metis: Ta dwójka komplikuje.

26 gru 17:00

Metis: Wynik 1/3?

26 gru 17:12

Jack: No to jak to zapisac... an = 2 + S_n a_n₊₁ = 2 + S_n₊₁ Czy nie

26 gru 17:13

Metis: Własnie tak to zapisałem i uzyskałem 1/3 , czyli wynik 333 ? emotka

26 gru 17:15

Metis: a_n=2+3+3²+...+3ⁿ /−2 a_n−2=3+3²+...+3ⁿ

	3
a_n−2=		(3ⁿ−1) /+2
	2

	3		1
a_n=		(3ⁿ−1)+2 =		(3ⁿ⁺¹+1)
	2		2

a_n+1=2+3+3²+...+3ⁿ⁺¹ /−2 a_n+1−2=3+3²+...+3ⁿ⁺¹

	3
a_n+1−2=		(3ⁿ⁺¹−1) /+2
	2

	3		1
a_n+1=		(3ⁿ⁺¹−1) +2 =		(3ⁿ⁺²+1)
	2		2

 1 
4*
(3n+1+1)
 2 

limn−>∞=

=

1 
(3n+2+1)
2 

2(3n+1+1)

limn−>∞=

1 
(3n+2+1)
2 

26 gru 17:44

Kacper: 0 pkt, bo to zadanie kodowane i liczy się wynik emotka

26 gru 19:50

Metis: Ale emotka

już koniec?

26 gru 19:53

Jack: Ja bym rozbił 3ⁿ⁺² na 3ⁿ * 3²

26 gru 19:54

Jack: Jak wroce do domu to wam napisze poprawny wynik xd

26 gru 19:58

Eta: A gdzie jesteś? Szukasz "gwiazdki"? emotka

26 gru 19:59

Jack: Gwiazdki i gwiazdko zbiorów coby bylo matematycznie

26 gru 20:01

Eta:

26 gru 20:13

Benny: Eta znajdzie jakieś dla mnie zadanie świąteczne?

26 gru 21:54

Jack: jaki jest wynik... zawsze 4/3 mi wychodzi

26 gru 22:28

5-latek: Benny może to rozwalisz dla mnie https://matematykaszkolna.pl/forum/310413.html

26 gru 23:23

Jack: hmm

26 gru 23:56

Kacper: Jack 0 pkt emotka

Nie czytacie poleceń emotka

27 gru 08:47

Jack: ale mi nie chodzi czy poleceniem jest zeby wpisac 333 czy 1,333 ale czy 4/3 to dobry wynik...liczylem 8 razy i ciagle ten wynik. Mam juz serdecznie dosc tego zadania ; )

27 gru 12:04

Kacper:

	4
Ta granica jest równa		.
	3

Ale odpowiedź jest inna emotka

Aczkolwiek rzeczywiście nie doprecyzowałem, czy chcę wynik 133 czy 333 emotka

27 gru 12:09

Kacper: Cały czas czeka na rozwiązanie zadanko z logarytmem emotka

I zaraz dam następne.

27 gru 12:09

Kacper: Kiedyś dałem to zadanko na forum i nie doczekało się rozwiązania emotka

Może się ktoś skusi emotka

Załoga złożona ze 175 robotników miała zbudować w określonym terminie odcinek autostrady A4. Po 30 dniach wspólnej pracy okazało się, że trzeba poprawić oddany wcześniej odcinek autostrady A2. Dlatego codziennie zabierano do tego zadania kolejnych 3 robotników, wskutek czego prace przy budowie autostrady A4 zakończono z 21‑dniowym opóźnieniem. W jakim czasie planowano pierwotnie wybudować dany odcinek autostrady A4?

27 gru 12:12

Jack: no, dziekuje bardzo ! czyli jednak dobrze obliczylem...

27 gru 12:12

Jack: co do tego logarytmu... wyznaczyc najmniejsza wartosc...hmm no dobra log₀_,₅ |x−1| − |4−x²| najpierw oczywiscie zalozenie |x−1| − |4−x²| > 0 4 przedziały... 1) (−∞ ; −2> − x + 1 − (−4 +x²) > 0 −x² −x + 5 > 0 ...

	−1 − √21		−1 + √21
x ∊ (		;		)
	2		2

Po uwzglednieniu dziedziny przedzialu

	−1 − √21
x ∊ (		; −2>
	2

juz nie bede tak rozpisywac tutaj, tylko wrzuce same koncowe przedzialy...

	−1 − √21
1) x ∊ (		; −2>
	2

	1−√13
2) x ∊ (−2;		)
	2

	−1 + √21
3) x ∊ (		; 2 >
	2

	1+√13
4) x ∊ (2 ;		)
	2

i teraz pytanie...czesc wspolna czy suma...hmmm dobra, obstawiam ze suma ; D no to ostatecznie :

	−1 − √21		1− √13		−1 + √21		1 + √13
x ∊ (		;		) U (		;		)
	2		2		2		2

dziedzine juz mam, no i super

27 gru 13:00

Jack: a dalej to juz nic nie zrobie... zabawa z logarytmem naturalnym?

27 gru 13:21

Kacper: Dziedzina się zgadza, teraz myśl co dalej emotka

Logarytmu naturalnego w lo nie ma, myśl inaczej.

27 gru 13:43

Jack: twoje "podpowiedzi" nic mi nie mowia ... emotka

zgaduje ze wynik to f_m_i_n (−2) = x i ta wartosc to nwm jak

	1
(		)^x = 3...
	2

27 gru 14:56

Kacper: Wymyśliłeś rozwiązanie, ale potrzebne uzasadnienie.

27 gru 15:37

Eta:

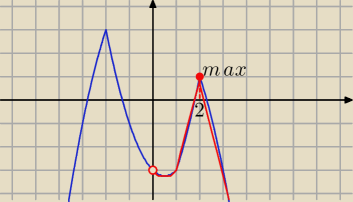
Kacper wpisał warunek: x>0 f(x) −−−− na rys funkcja logarytmiczna jest malejąca to osiąga najmniejszą wartość dla największego argumentu zatem dla x=2 , y_max= 1

	1
log{0,5) f(x)=1 to y_min=
	2

27 gru 15:54

Jack: potem powiedzial ze ten warunek sie jednak nie liczy... a ja nie narysuje wykresu z dwoma wartoscmi bezwzglednymi... ; d

27 gru 16:06

Eta: Źle podstawiłam ( wszystko przez to,że jestem przeziębiona i głowa mnie boli ) emotka

log{0,5)1= 0 ⇒ y_min=0

27 gru 16:25

5-latek: Dobry wieczor Eta emotka

Wracaj szybko do zdrowia emotka

27 gru 16:27

Eta: Skoro x>0 −− się nie liczy to dla x= −2 y_max=3 wtedy log_0,53= y_min=...

27 gru 16:29

Jack: no i tak zrobilem... dla x = −2 y max = 3 wiec ymin ... i z tego co widze w wolframie to zespolone mi sie pojawily ; D

27 gru 16:32

Jack: btw. skoro Cie glowa boli to nie rozwiazuj zadan z matmy tylko sie poloz i odpocznij emotka

27 gru 16:33

Eta: Witam "małolatku" emotka

Muszę się wykurować bo Sylwester tuż,tuż ......

27 gru 16:33

Eta: Zadania to dla mnie jak "balsam".......... na wszystko emotka

27 gru 16:34

5-latek: A ja wlasnie swojej żonie kupiłem balsam czekoladowy do ciała

27 gru 16:37

Jack: trzeba bylo jej dac troche zadan do policzenia? xD

27 gru 17:00

Kacper: W sumie z warunkiem czy bez zadanko jest rozwiązywalne emotka

Jack co to znaczy, że nie umiesz narysować wykresu funkcji z wartością bezwzględną?

28 gru 08:51

Jack: Z suman/ roznica wartosci bezwzglednych....

28 gru 11:21

Jack: |x−1| − |4−x²| Jestem bardzo ciekaw jak Ty bys to narysował

28 gru 11:25

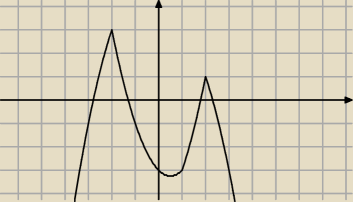
Benny: rysunek

28 gru 11:30

Jack: Jedyne co wiadomo to ze albo dla 2 albo dla −2 jest max bo wtedy wyrazenie z minusem przed wartoscia bezwzgledna wynosi 0... A jak podstawimy to widac ze dla minus 2 osiagnie wieksza wartosc a dokladniej rowna 3...

28 gru 11:32

Jack: @Benny Wpisac w jakikolwiek program do rysowania to ja tez umiem

28 gru 11:32

Benny: Chcesz narysować dokładny wykres? Jak już wcześniej robiłeś, rozbij na przedziały i przebieg zmienności funkcji emotka

28 gru 11:42

Jack: To bym mysial podstawiac a podstawoac...

28 gru 12:03

Jack: Dobra mniejsza... Niech ktos mi teraz odpowie ile to jest

	1
(		)^x = 3
	2

28 gru 12:05

Benny: log_1/23=x

28 gru 12:35

Jack: no i ile ten "x" wynosi... ?

28 gru 15:25

Eta:

	log3		0,4771
x=		≈		≈ −1,58504983388
	log0,5		−0,3010

28 gru 15:31

Kacper: Jack nie marudź, że nie umiesz paraboli i prostych narysować

28 gru 15:48

Jack: no umiem, ale to trza tylko gawalek paraboli wszedzie : D

28 gru 15:54

Jack: Kacper, wynik Ety jest poprawny?

28 gru 15:55

Benny: Kawałek paraboli wszędzie? @Kacper a to nie będzie cześć hiperboli i prosta?

28 gru 16:00

Kacper: Benny twierdzisz, że w wyresie funkcji f(x)=|x−1|−|4−x²| są kawałki hiperboli?

28 gru 16:53

Kacper: Jack wynik Ety jak najbardziej ok, ale mnie satysfakcjonuje dokłada wartość, czyli log_0,53.

28 gru 16:55

Jack: paraboli

@Kacper to zrobilem tak...

28 gru 17:09

Benny:

	1
@Kacper chodziło mi o wykres (		)^x oraz y=3
	2

28 gru 17:26

henrys: @Kacper rozwiązanie Twojego zadania to 58 dni, skąd to zadanie?

29 gru 02:21

Kacper: henrys emotka

(o ile nie znalazłeś mojego wpisu z wynikiem na innym forum

) Zadanko z jakiegoś konkursu matematycznego jak dobrze pamiętam emotka

29 gru 08:49

betus: @Kacper czy jest możliwość uzyskania od Ciebie arkuszy z matury WSiP z listopada 2015

25 lut 20:37

Jack: oto jest pytanie... kto mi upuje posta

25 lut 20:44

Damian: jak zobaczyłem co tu się wyprawia to straciłem jakąkolwiek wiare że napiszę tę mature na chociaż+− 50% emotka

25 lut 20:53

Eta:

25 lut 21:57

Krzysiek: Poproszę zadanie dla I klasy liceum emotka

26 lut 09:08

Jack: Znajdz dziedzine funkcji

	√(x+6)
f(x) =
	(x²−4)√(3−x)

26 lut 17:16

Krzysiek: (x²−4)√(3−x)≠0 (x²−4≠0) ∨ (√(3−x)≠0) ∨ (x²−4≠0 ∧ √(3−x)≠0) x≠2 ∧ x≠−2 3−x≥0 ⇒ x≤3 x≠2 ∧ x≠−2 ∧ x≤3 Odpowiedź: x∊(−∞;−2)U(−2;2)U(2;3>

26 lut 20:04

Jack: nwm czy /\ \/ te znaczki sie zgadzaja... ale brakuje jeszcze czegos...bez tego jest wynik bledny emotka

w sensie jeszcze jedno zalozenie...

26 lut 20:33

Jack: i jak masz √3−x ≠ 0 to raczej 3 − x > 0 a nie ≥ 0 bo nie ma byc zerem emotka

26 lut 20:35

Krzysiek: Faktycznie, powinno być > .. D_f = x∊(−∞;−2)U(−2;2)U(2;3> ?

26 lut 20:45

Jack: nie nie, chodzilo mi o spojrzenie na licznik

26 lut 20:45

Krzysiek: Df = x∊(−∞;−2)U(−2;2)U(2;3)

26 lut 20:46

Krzysiek: x+6≥0 x≥−6 emotka

26 lut 20:46

Krzysiek: Df = x∊(−6;−2)U(−2;2)U(2;3)

26 lut 20:47

Jack: no więc ostatecznie dziedzina... =

26 lut 20:47

Jack: heh, zapisales x ≥ −6 (20:46) a w dziedzinie otwarty...(20:47) oczywiscie D_f = <−6;−2) U (−2;2) U (2;3)

26 lut 20:48

Krzysiek: Zwykłe rozkojarzenie emotka

Masz jeszcze jakieś?

26 lut 20:51

Jack: mowimy o calej 1wszej klasie? i czy zadanka maja byc raczej trudniejsze czy latwiejsze

26 lut 20:54

Krzysiek: Cała pierwsza klasa, wielomiany, mogą być jakieś łatwe zadania konkursowe, typu udowodnj, że coś jest podzielne przez jakąś liczbę ale nie tylko takie

26 lut 20:59

Jack: wielomiany ja mialem w drugiej to Ci nie dam

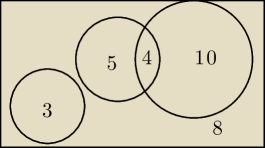
W 30−osobowej klasie 14 uczniow ma psa, 9 − kota, 3−swinki morskie, a 8 nie ma zadnego z wymienionych zwierzat. Uczniowie majacy swinki morskie nie maja innych zwierzat. Podaj, ilu uczniow ma jednoczesnie psa i kota

26 lut 21:07

Krzysiek: −4

26 lut 21:20

Mila: Załóżcie nowy wątek.

26 lut 21:21

Jack: −4 w sensie ze 4? Milu dlaczego nowy?

26 lut 21:27

Benny: Jest bardziej przejrzyściej emotka

Tylko nie rób więcej niż 100 postów, bo Eta czeka

26 lut 21:44

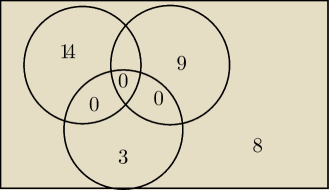
Krzysiek: rysunek

3 osoby mają świnki, nie mają oni innych zwierząt (trzy zera na rysunku) 9 osób ma kota, 14 ma psa 22−14−9−3 = −4, więc coś się nie zgadza

26 lut 21:54

Jack:

26 lut 22:11

Krzysiek: Faktycznie... Taki układ równań mógłby by być:

⎧	x+y=9
⎨	y+z=14
⎩	x+y+z=19

y=4, x=5, z=10

26 lut 22:50