geometria analityczna xxxy: Punkt C(1,−3) jest wierzcholkiem trojkata rownobocznego ABC, zaś punkt S(3,−1) jest środkiem okręgu wpisanego w ten trojkat. Wyznacz wspolrzedne wierzcholkow A i B.

Eta: https://matematykaszkolna.pl/forum/45570.html

xxxy: To inne zadanie

5-latek: Należy sobie przypomnieć wiadomości z geometrii elenmtarnej 1. Gdzie lezy srodek okręgu wpisanego w trojkacie (ogolnie ) 2. czym jest dwusieczna kata w trojkacie równobocznym ? tak na marginesie srodkowa tez to tez powinno pomoc https://matematykaszkolna.pl/strona/856.html

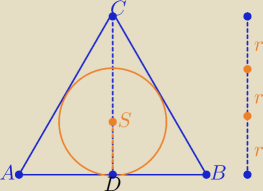
Eta: Zadanie prawie takie samo ..... tylko nie myślisz

	1
wektor DS=		SC
	2

SC=[−2,−2] to DS=[−1,−1]=[3−x_D, −1−y_D] ⇒ D(4,0)

	yC−yD
prosta AB ⊥DC aDC=		= 1
	xC−xD

to AB: y=−1(x−x_D)+y_D ⇒ AB : y=−x+4 i dalej jak w podanym linku bo masz tam prostą AB: y= −x+4

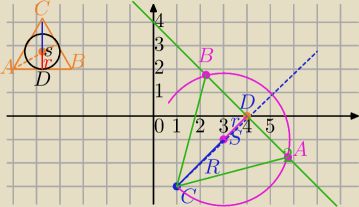
Mila: C(1,−3) ,S(3,−1) CS=2r CS^→=[2,2]

1		1
	CS→=		*[2,2] =[1,1]
2		2

S=(3,−1)→T{[1,1]⇒D=(3+1,−1+1)=(4,0) D jest środkiem AB, CD⊥AB Prosta CD jest postaci: y=x+b Prostopadła do niej ma równanie: k: y=−x+b i D∊k 0=−4+b⇔b=4 k: y=−x+4 Kreślimy okrąg opisany na ΔABC R=2√2 (x−3)²+(y+1)²=(2√2)² Przecięcie prostej y=−x+4 to punkty A i B Rozwiąż układ równań: (x−3)²+(y+1)²=8 y=−x+4

5-latek: Czyli korzystamy z tego z tego ze srodek okręgu wpisanego w trojkat równoboczny jest także srodkiem okręgu opisanego na trojkacie równobocznym

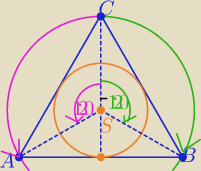
Eta: Najprostszy sposób Kiedyś uczono w szkole ( obrotu punktu dookoła innego punktu o kąt α Szkoda,że takiego wzoru nie umieszczono w tablicach wzorów maturalnych S(3,1) , C(1,−3) dokonując obrotu punktu C o kąt 120^o względem punktu S otrzymamy punkt A dokonując obrotu punktu C o kąt −120^o względem punktu S otrzymamy punkt B Równania takiego obrotu to: x_A= (x_C−x_S)*cosα − (y_A−y_S)*sinα+ x_S y_A= (x_C−x_S)*sinα + (y_A−y_S)*cosα +y_S cos120^o=cos(−120^o)= −1/2 i sin120^o= √3/2 i sin(−120^o)= −√3/2 otrzymujemy: x_A= (1−3)*(−1/2)−(−3+1)*√3/2+3 = ..... = 4+√3 y_A= (1−3)*√3/2+(−3+1)*(−1/2) −1=.... = −√3 A( 4+√3, −√3) podobnie dla B ..................

5-latek: Eta No niestety nie ma

Eta: Sprawdzamy S −−− jest środkiem ciężkości tego trójkąta ( wzór jest w tablicach)

	xA+xB+xC		yA+yB+yC
xS=		i yS=
	3		3

A(4+√3, −√3) dla B otrzymujemy B ( 4−√3, √3) , C(1, −3) i S( 3, −1)

	4+√3+4−√3+1		9
to: 3=		=		= 3 jest ok
	3		3

	−√3+√3−3
−1=		= −1 jest ok
	3

xxxy: Dziekuje wszystkim za pomoc

Eta: