Pomocy Aga: Punkt C = (1,−3) jest wierzcholkiem trojkata rownobocznego ABC. Wyznacz wspolrzedne pozostałych wierzcholkow trojkata, wiedząc ze należą one do prostej o rownaniu y= −x + 4

Aga: Pomocy

Aga: Halo

Godzio: pomoge

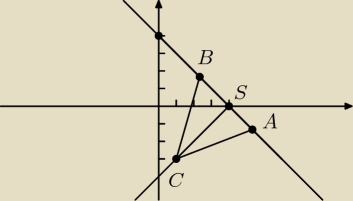
Godzio: Prosta prostopadła do prostej y = −x + 4 , przechodząca przez C −3 = 1 * 1 + b −3 = 1 + b b = − 4 y = x − 4 punkt przecięcia obu prostych to środek odcinka AB x − 4 = −x + 4 2x = 8 x = 4 y = 0 S(4,0) odległość SC to wysokość: SC = √(4−1)² + (−3−0)² = √9 + 9 = 3√2

	a√3
h =
	2

6√2 = a√3

	6√6
a =		= 2√6
	3

√6 = SB = SA √(4−x)² + (0 − y)² = √6 /² i podstawiam prostą y = −x + 4 16 − 8x + x² + 16 − 8x + x² = 6 2x² − 16x + 26 = 0 x² − 8x + 13 = 0 Δ=12

	8 − 2√3
x1 =		= 4 − √3
	2

	8 + 2√3
x2 =		= 4 + √3
	2

x = 4 − √3 => y = √3 x = 4 + √3 => y = −√3 A(4 + √3 , −√3) B(4 − √3 , √3)