Ile miejsc zerowych ma ta funkcja?
Lukas94: (x2 −1)(x2 −4)(x2 +9}(x−1)2(x+2)2
potrafiłby ktoś zrobić ten przykład?
30 paź 23:20
mat:
x∊{−3,−1,2,3}
30 paź 23:23
Qulka: tylko −1 i 2 w ostatnim nawiasie jest +

30 paź 23:26
Lukas94:
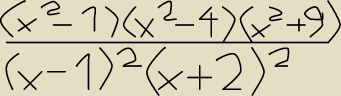
narysowałem przykład by był lepiej widoczny
30 paź 23:29
Lukas94: prosiłbym aby tu ktoś napisał wszystkie obliczenia, bo ja nie potrafię obliczyć tego przykładu
a wasze obliczenia dużo by mi pomogły.
30 paź 23:31
mat:
jeżeli ostatni nawias (x2+9)
odp x∊{−1,2}
30 paź 23:33
30 paź 23:33
30 paź 23:35
Lukas94: nie chodzi mi o odpowiedź, tylko chodzi mi o obliczenia, chciałbym zobaczyć jak rozwiązać
dziedzinę z tego przykładu,
30 paź 23:35
Lukas94: jaki znak należy wstawić pomiędzy (x−1)2 a 0 podczas obliczania dziedziny ?
30 paź 23:38
Mila:
Zał.
x−1≠0 i x+2≠0⇔
x≠1 i x≠−2
Miejsca zerowe:
(x2−1)*(x2−4)*(x2+9)=0⇔
x2−1=0 lub x2−4=0 lub
x2+9=0 to równanie nie ma rozwiązania w zbiorze R, bo x2+9>0 dla każdego x∊R
(x−1)*(x+1)=0 lub (x−2)*(x+2)=0⇔
x−1=0 lub x+1=0 lub x−2=0 lub x+2=0⇔
x=1∉D lub x=−1 lub x=2 lub x=−2∉D
M.z:
x=−1,x=2
30 paź 23:39
Lukas94: przy obliczaniu dziedziny między (x−a)2 a 0, i między (x+a)2 a 0, jest taki sam znak?
30 paź 23:44
Lukas94: dziękuję "Mila" za obliczenia.
30 paź 23:49
Mila:
Nie rozumiem Twojego pytania z 23:44
Mianownik ma być różny od zera.
(x−1)2≠0⇔x−1≠0⇔x≠0
30 paź 23:52
Lukas94: zapytam inaczej, czy przy obliczaniu dziedziny z mianownika niezależnie od tego czy byłoby
(x−a)2, czy byłoby (x+a)2 miedzy tym wyrażeniem a zerem jest znak ≠ ?
30 paź 23:59
Qulka: nawet jak tam będzie log(x) albo sin(x) to będzie znak ≠

31 paź 00:00
Qulka: po prostu nie wolno dzielić przez 0

więc mianownik zawsze musi być ≠ 0
31 paź 00:01
Lukas94: rozumiem, dziękuję,
31 paź 00:02

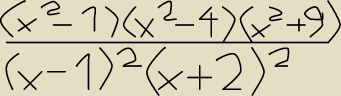 narysowałem przykład by był lepiej widoczny
narysowałem przykład by był lepiej widoczny

 więc mianownik zawsze musi być ≠ 0
więc mianownik zawsze musi być ≠ 0