Monotoniczność Qazz: Zbadać monotoniczność i wypukłość funkcji f oraz wyznaczyć jej lokalne ekstrema i punkty przegięcia:

	1
f(x)=e1x (nie wiem czy dobrze widać, ale to e do potęgi		)
	x

daras: https://matematykaszkolna.pl/strona/381.html

daras: https://matematykaszkolna.pl/strona/387.html

daras: https://matematykaszkolna.pl/strona/359.html

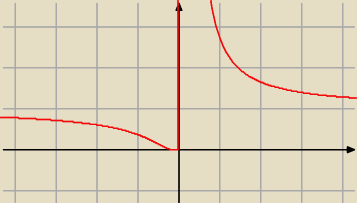
Janek191: f(x) = e^1_x ; x ≠ 0

	e1x
f '(x) = −		< 0 , więc funkcja jest malejąca
	x2

w przedziałach: ( − ∞, 0) , (0 ; +∞)

Qazz: Może głupie pytanie, ale czasem mam problem z narysowaniem funkcji, np tutaj. skąd znasz jej kształt? Po policzeniu ekstremów/punktów lokalnych, czy też podstawiasz jakieś przykładowe wartości x i Ci wychodzi? Czy jakoś jeszcze inaczej?

Janek191: Funkcja f jest wklęsła w ( −∞ ; 0), a jest wypukła w ( 0 ; +∞)

Janek191: Tu niżej jest program do rysowania wykresów funkcji. Patrz na: rysuję

Qazz: Ale jak brak programu? W sensie masz to na kolokwium?

Janek191: To trzeba po kolei wyliczać wszystko. 1) dziedzina 2) pochodna f '(x) f '(x) > 0 ⇒ f rośnie f '(x) < 0 ⇒ f maleje 3) ekstrema f (x_o) = 0 i zmienia znak w x_o itd.

Qazz: oki, dzięki