wyznaczanie suriekcji kamil: Jeśli mam wyznaczyć liczbę suriekcji ze zbioru {1,2,3,4,5,6,7,8,9,10} na {1,2} to muszę policzyć wszystkie takie kombinację,że np. 1 należy do 1, a liczby w przedziale <2,10> należą do 2?

kamil: będzie ich 10*9 = 90?

PW: Co to znaczy "1 należy do 1, a liczby (...) należą do 2"? Suriekcja to funkcja, i w tych terminach musisz o tym opowiadać.

kamil: 1 jest na 1

PW: kamil, odpowiadasz niesensownie. Czy umiesz wyznaczyć liczbę funkcji f: {1, 2, 3, ..., 10} → {1, 2} ? Idzie o liczbę wszystkich funkcji, bez żadnych dodatkowych określeń, jest na to odpowiednie twierdzenie w kombinatoryce.

kamil: niestety, ale nie wiem

kamil: 1 może należeć zarówno do 1 jak i 2, tak jak reszta liczb z tego zbioru f

henrys: suriekcja to funkcja, zatem dla każdego elementu zbioru A={1,2,3,4,5,6,7,8,9,10} przyporządkowuje jeden i tylko jeden element zbioru B={1,2}, ale w ten sposób, że w zborze A istnieje taki element, któremu zostaje przyporządkowana 1 i taki, któremu przyporządkowana jest 2. Ile jest takich suriekcji? dla każdego elementu ze zbioru A możemy przyporządkować 1 lub 2 więc 2*10, ale w takim razie mogłoby się zdarzyć, że wszystkim el. przyporządkujemy 1 lub wszystkim el. przyp.2. więc ilość suriekcji to 2*10−2=18

henrys: kurde popieprzyłem 2¹⁰−2

PW: A w kombinatoryce 2¹⁰ to liczba 10−elementowych wariacji (z powtórzeniami) o wartościach w zbiorze dwuelementowym, nie uczyłeś się tego w szkole średniej? Przykład takiej wariacji: (1,2,2,2,2,1,2,1,1,2). Zapisuje się to jako ciąg dziesięcioelementowy, w którym wyrazy mogą być tylko jedynką lub dwójką (same jedynki lub same dwójki też mogą się zdarzyć). Tak jest wygodniej niż pisać f(1) = 1, f(2) = 2, f(3) = 2, f(4) = 2 itd. aż do f(10) = 2.

henrys: pomyłka, to będą kombinacje z powtórzeniami zbioru 10 el. ze zbioru 2−el.

11 2
	=55

nie myślę...

henrys: nie, jakiegoś ciołka złapałem

henrys: dobra ile to już policzcie bo ja się nie dolliczę dzisiaj ale to jest suriekcja więc nie może być samych 2

PW: Myślę, że było dobrze, kamil dzisiaj każdego skołuje

PW: Od liczby wszystkich możliwych funkcji odjąłeś dwie, które nie są "na", 2¹⁰ − 2 to dobry wynik.

henrys: tak, wiem wiem ale jakiejś zaćmy dostałem

kamil: ale dlaczego tak ?

PW: Odpowiedz, kamilu − uczyłeś się o wariacjach, permutacjach i kombinacjach w szkole średniej?

kamil: już nie wiele z tego pamiętam.

kamil: 2¹⁰ to rozumiem bo każdą z liczb można wstawić na 2 sposoby, ale czemu −2?

PW: Chciałeś liczyć suriekcje, czyli funkcje przyjmujące obie wartości − dlatego trzeba było odjąć liczbę funkcji, które przyjmują tylko wartość 1 i liczbę funkcji przyjmujących tylko wartość 2 (czyli dwie funkcje należało odrzucić). Musisz powtórzyć to co było w szkole, bo na studiach tego po prostu wymagają, nikt nie będzie tłumaczył takich prostych rzeczy.

Mila: Funkcja musi przyjmować wszystkie wartości ze zbioru {1,2}. Odejmujesz sytuację, gdy masz dwie funkcje stałe. Jedna z nich: f(x₁)=1 f(x₂)=1 . . . (x₁₀=1 bo wtedy zostaje wartość 2 nie "wykorzystana" Druga funkcja stała to: f(x₁)=2 f(x₂)=2 . . . f(x₁₀)=2 bo wtedy zostaje wartość 1 nie "wykorzystana". Wszystkich przyporządkowań jest 2¹⁰ więc 2 sytuacje nie spełniające warunków zadania odejmujemy. Stąd wynik 2¹⁰−2.

kamil: dla x=1,x=2 odejmuje sie te sytuacje?

PW: Interesują Cię suriekcje, czyli funkcje "dwuwartościowe" (przyjmujące zarówno wartość 1, jak i wartość 2). Ze wszystkich funkcji tylko dwie są "jednowartościowe" − ta przyjmująca tylko wartość 1 dla wszystkich 10 argumentów i ta przyjmująca tylko wartość 2. K O NI I E C

Mila: Dla wszystkich argumentów przyjmowana jest wartość 1 albo dla wszystkich argumentów przyjmowana jest wartość dwa. Tak jakby 10 osób wsiadło do pierwszego wagonu a mieli polecenie jakoś rozdzielić się, albo 10 osób wsiadło tylko do drugiego wagonu.

kamil: ale 1 ze zbioru A do 1 ze zbioru B nie może należeć?

Nuti: @kamil 1 ze zbioru A nie ma nic wspólnego z 1 ze zbioru B. Żeby nie było tego zamieszania, oznacz sobie elementy zbioru A przez x₁ i x₂, a elementy B przez 1,2,...,10, to ci się nie będzie mieszać co jest czym.

kamil: x₁ =1, więc nie może zawierać elementu 1 ze zbioru B, tak to rozumiem i dlatego jest −2

Nuti: @kamil nie, to nie o to chodzi. Chodzi o to, że twoje funkcje muszą być NA, czyli wszystkie wartości w zbiorze 1, 2 muszą być wykorzystane. Odejmujesz dwie funkcje stałe (pierwsza: wartość funckcji na wszystkich argumentach jest 1, druga: wartość funkcji na wszystkich elementach jest równa 2) − bo wtedy ta druga wartość nie występuje i nie masz funkcji NA. Przy okazji: widzę, że źle napisałam o 9:45. Myśl o dziedzinie jako o punktach x₁,x₂,...,x₁₀ a o wartościach jako 1 i 2. To nie o to chodzi, że wartość w x₁ nie może być 1 (może!), tylko że nie chcesz liczyć funkcji, w których wartość dla WSZYSTKICH dziesięciu argumentów jest równa 1, bo wtedy 2 nie występuje jako wartość, czyli nie mamy surjekcji. A w twoim zadaniu liczysz ile jest surjekcji. Kapisz?

kamil: chyba zaczynam rozumieć jeśli miałbym taki zbiór: {1,2,3,4,5} na {1,2,3} to liczba suriekcji 2⁵ − 3?

Nuti: 3⁵ − 3 bardzo słusznie odjąłeś trzy funkcje stałe, ale wszystkich funkcji ze zbioru 5−elem do zbioru 3−elem jest 3⁵ a nie 2⁵ (2⁵ to do 2−elem). Bo na każdym miejscu możesz mieć jedną z 3 wartości, czyli funkcji jest 3*3*3*3*3. No i odejmujesz 3 funkcje stałe.

Nuti: Oj, nie! źle napisałam! Przecież jeśli wartościami będą np. 1, 2 i 2 to też nie będzie surjekcji, bo brakuje 3 w zbiorze wartości! To jest trochę bardziej skomplikowane, ale ja teraz muszę jechać. Później coś napiszę!

kamil: 3⁵ − 6?

henrys: 3⁵−2*2⁵−3 3⁵ to wszystkie, 2⁵ to te w których brak jednego elementu, 3 to te w których występują tylko 1 albo tylko 2 albo tylko 3.

henrys: aj jak zwykle 3⁵−3*2⁵−3 rozumiesz?

kamil: nie, skomplikowany ten zapis.

henrys: wyjaśniłem co oznacza każdy składnik

kamil: ale czemu 2⁵ − 3? a nie 2⁵ −2 jak wtedy zabierasz ze zbioru jednąwartość?

henrys: 3⁵−3*2⁵−3 3*2⁵− to liczba suriekcji,w których nie występuje jedna z liczb 1, 2 lub 3 np. {1,1,2,1,2} brak trójki teraz, dlaczego jeszcze −3 1 sytuacja {1,1,1,1,1} 2 {2,2,2,2,2} 3 {3,3,3,3,3}

henrys: liczba funkcji nie suriekcji

PW: To i tak jest jeszcze źle

henrys: a już widzę wśród tych 3*2⁵ mogą się znaleźć te (1,1,1,1,1), (2,2,2,2,2), (3,3,3,3,3) masz rację zatem powinno być 3⁵−3*2⁵+3

Mila: Liczba suriekcji: ============= X={x₁,x₂,....x_n} Y={y₁,y₂,....y_k} 1^o n<k nie ma suriekcji 2^o n=k− Bijekcja n! liczba bijekcji pomiędzy zbiorami o liczebności n 3^o n>k Liczba suriekcji:

	k j
Sn,k=∑(j=0 do k) (−1)j*		*(k−j)n

=================================== Dla k=2 i k=3 można łatwo obliczyć stosując metodę wyłączeń. Spróbujemy z wzoru ( dowód pewnie miałeś na wykładzie− trudny). 1) n=10, k=2

	2 j
S10,2=∑(j=0 do 2)(−1)j*		*(2−j)10=

	2 0		2 1		2 2
=(−1)0*		*(2−0)10+(−1)1*		(2−1)10+(−1)*		*(2−2)10=

( ostatni wyraz sumy to 0) =2¹⁰−2 2) n=5 k=3

	3 j
S5,3=∑(j=0 do 3)(−1)j*		*(3−j)5=

	3 0		3 1		3 2
=(−1)0*		*(3−0)5+(−1)1*		*(3−1)5+(−1)2*		*(3−2)5=

=3⁵−3*2⁵+3

kamil: wśród tych 3*2⁵ + 3 mogą się znaleźć te (1,1,1,1,1), (2,2,2,2,2), (3,3,3,3,3) ale przecież wszystkie wartości muszą przyjmować jakiś argument. To dlaczego dodajesz to,że każdy argument może by = 1?

Mila: Do jakiego wpisu to pytanie?

henrys: a ja mam wrażenie (mam nadzieje, że mylne), że kamil nie wie co to jest funkcja

kamil: do wpisu henrysa z 11:57

kamil: wiem co to funkcja, ale przecież w suriekcji nie może zostać nie przydzielona wartość (1,1,1,1,1) − w tym przypadku zostają dwie nie przydzielone wartości ( 2 i 3)

kamil: dobra chyba źle zinterpretowałem ten znak +3, dla wyznaczenia suriekcji zbioru {1,2,3,4,5} na {1,2,3,4} jest ich: 4⁵ − 4* 3⁵ ?

kamil: 4⁵ − 4 * 3⁵ + 4

henrys: dobrze, że wiesz, bo inaczej, wszystkie te wpisy nie miałyby sensu 2⁵ to ilość wszystkich funkcji typu (1,1,2,1,2) bez trójki (w tym również (1,1,1,1,1) i (2,2,2,2,2) 2⁵ to ilość wszystkich funkcji typu (1,3,3,1,1) bez dwójki (w tym również (1,1,1,1,1) i (3,3,3,3,3) 2⁵ to ilość wszystkich funkcji typu (2,3,2,3,3) bez jedynki (w tym również (2,2,2,2,2) i (3,3,3,3,3) teraz od ilości wszystkich funkcji =3⁵ odejmujemy 3*2⁵ (ale wtedy dwukrotnie odejmujemy każdą z takich jak (1,1,1,1,1) dlatego dodajemy 3

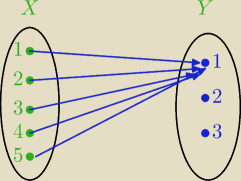
Mila: Do zadania: {1,2,3,4,5} na {1,2,3} to liczba suriekcji . ================================= Kamil przecież podałam Ci wzór i wynik jest taki sam jak u henrysa. Nie możesz tak opisać funkcji, dlatego, że ciąg wartości (1,1,1,1,1) oznacza takie przyporządkowanie jak na rysunku: a to nie jest suriekcja.

kamil: wiem, czyli przykład z 16:00 dobrze rozwiązałem?

henrys: przeczytaj co napisałem dla poprzedniego przykładu lub skorzystaj ze wzoru, który podała Mila i zapisz poprawnie

kamil: Dla przykładu {1,2,3,4,5} na {1,2,3,4}: 4⁵ − 4 * 3⁵ + 4 4⁵, bo każdy argument można wstawić na 4 sposoby odejmujemy od tego: 4 * 3⁵ + 3 ?

kamil: 4⁵ − 4 * 3⁵ + 4 − czemu to jest źle?

Mila: Inny sposób niż wzór. X={1,2,3,4,5} Y={1,2,3} Wyobraź sobie, że masz 5 ponumerowanych kul i masz 3 ponumerowane szuflady. Rozkładasz te kule do 3 szuflad tak ,aby żadna nie była pusta. Np. k1 do s3 k2 do s2 k3 do s3 k₄ do s1 k5 do s2 Masz ciąg wartości (3,2,3,1,2) czyli f(1)=3 f(2)=2 f(3)=3 f(4)=1 f(5)=2 Ile będzie wszystkich możliwości ? 1) jedna szuflada pusta

3 2
	*(25−2) wybieram dwie szuflady i do nich wkładam kule, tak, aby żadna nie była pusta

2) dwie szuflady puste, wszystkie kule wkładam do jednej szuflady

3 1
	*1=3 − wybór szuflady i tylko na jeden sposób wszystkie wkładam.

To są sytuacje , które nam nie odpowiadają. 5 ponumerowanych kul możesz włożyć do 3 szuflad na 3⁵ sposobów. Stąd : Liczba suriekcji: 3⁵−[3*(2⁵−2)+3]= =3⁵−[3*2⁵−6+3]=3⁵−3*2⁵+3

kamil: a dla tego przykładu z 16:15 jak powinien wyglądać zapis?

kamil: Mila byś mogła jeszcze zerknąć tu: https://matematykaszkolna.pl/forum/298619.html i tu: https://matematykaszkolna.pl/forum/298642.html ?

Mila: 16:00 źle. f: {1,2,3,4,5} na {1,2,3,4}: Liczba suriekcji:

5 2
	*4!

To samo możesz obliczyć z wzoru, który podałam.

kamil:

k j
	*(k−j)n

o ten wzór chodzi ?

kamil: za bardzo nie wiem gdzie tam ten wzór się zaczyna i kończy

Mila: Przeanalizuj dwa rozwiązane przykłady ( i po co ja to pisałam?) k

	k j
Sn,k=∑ (−1)j*		*(k−j)n

j=0 licz dla n=5 i k=4

Kacper:

Mila: Co to Kacperku?

kamil: Sprobowałem wyznaczyć ilość suriekcji wzorem Mili: dla przykładu: {1,2,3,4,5} na {1,2,3,4}

	4 j
Sn,K = ∑(j = 0 do 4)(−1)j *		(4j)5

	4 0		4 1
(−1)0 *		(4 − 0)5 + (−1)1 *		(4 − 1)5 +

	4 2		4 3
(−1)2 *		(4 − 2)5 + (−1)3 *		(4 − 3)5

	4 4
+ (−1)4 *		(4 − 4)5 =

= 4⁵ − 4*3⁵ + 6 − 4 = 4⁵ − 4*3⁵ − 2 Dobrze?

kamil: + 2 na końcu powinno być

kamil: źle wyliczyłem, powinno być: 4⁵ − 4*3⁵ + 6 * 2⁵ − 4

Mila: Dobrze, (19:32) teraz wynik.

kamil: jednak wzór się przydał, na początku wydawał się zbyt skomplikowany.

Mila:

kamil: Mila wiesz jak wyliczyć taki symbol newtona co jest tutaj: ? https://matematykaszkolna.pl/forum/298642.html