Oblicz długość odcinka łączącego punkty styczności. Leo: Przez punkt A(3,−4) poprowadzono styczne do okręgu o środku S(3,1) i promieniu √5. Oblicz długość odcinka łączącego punkty styczności.

daras: W czym problem?

daras: podstaw r−nia prostych do okręgu a potem: https://matematykaszkolna.pl/strona/1248.html

6xdj: walnij kolego sobie najpierw rysunek

Leo: Odległość między punktami to ja umiem obliczyć, tylko jak wyznaczyć te punkty?

daras: a r−nie prostej umiesz napisać? https://matematykaszkolna.pl/strona/1223.html

Leo: Równanie prostej przechodzącej przez 2 punkty? Ale skąd mam wziąć te punkty? Mam tylko podany punkt A i S.

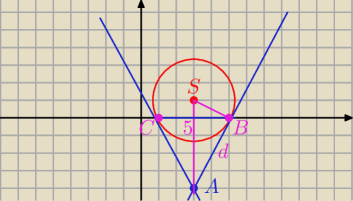
Janek191: I AS I = 5 I SB I = √5 zatem d² + (√5)² = 5² d² = 25 − 5 = 20 B = (x; y) d² = IABI² = (x −3)² + (y +4)² = 20 oraz z równania okręgu ( x − 3)³ + ( y −1)² = 5 Odejmujemy stronami y² + 8 y + 16 − ( y² − 2y + 1) = 20 − 5 10y +15 = 15 y = 0 === x² − 6 x + 9 + 16 = 20 x² − 6 x + 5 = 0 Δ = 36 − 20 = 16 √Δ = 4

	6 − 4		6 + 4
x=		= 1 lub x =		= 5
	2		2

więc C = ( 1; 0) oraz B = ( 5; 0) czyli I BC I = 5 − 1 = 4 ===============

Leo: Dziękuję bardzo.

Janek191: Tam w równaniu okręgu powinno być oczywiście: ( x −3)² + (y − 1)² = 5