jednokładność Shadowplay: Wyznacz obraz podanej prostej w jednokładności o środku S i skali k. y=4x−1 S(0,2) k= −3

daras: https://matematykaszkolna.pl/forum/159195.html

daras: korzystanie z gugla nie boli

majka: https://matematykaszkolna.pl/forum/151018.html S(a,b) skala k

Shadowplay: Dzięki za linki c:

Shadowplay: Jednak odświeżam temat, gdyż linki nie pomogły. Umiałabym zrobić to zadanie, gdyby środek jednokładności był w punkcie S(0,0), ale dla (0,2) nie wiem, jak to ruszyć

Eta: https://matematykaszkolna.pl/forum/151018.html Zobacz rozwiązania podane przez Mila

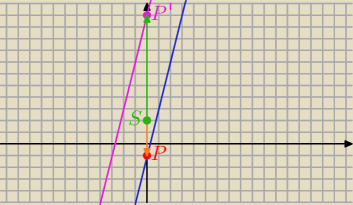
Mila: Witaj Eta, wypoczęta po upałach? Można odczytać od razu z rysunku. Można skorzystać z metody ogólnej z linku. Albo wprost z definicji i własności figur jednokładnych. Obrazem będzie prosta równoległa: y=4x+b Obieramy punkt na prostej k: y=4x−1 P=(0,−1), P'=(x,y) S=(0,2) SP'^→=[x−0,y−2] SP^→=[0,−3] SP'→=^def k*SP^→ [x,y−2]=−3*[0,−3] [x,y−2]=[0,9] x=0 i y−2=9⇔ x=0 y=11 P'=(0,11) 11=4*0+b b=11 y=4x+11

Shadowplay: Jeżeli S=(a,b) środek jednokładności k− skala jednokładności to x'=kx+a*(1−k) y'=ky+b*(1−k) To (1−k) to ogólna zasada działająca w przypadkach, gdy środek nie jest w punkcie (0,0)? Przepraszam, za takie wydłużanie, ale czy da się to jakoś wytłumaczyć dlaczego 1−k?

Shadowplay: Przepraszam, mam problem z internetem. Dziękuję bardzo Mila za cierpliwość i poświecenie

Mila: Wzór wyprowadzasz z definicji jednokładności. P=(x,y), P'=(x',y'), S=(a,b) SP'^→=^defk*SP^→⇔ [x'−a,y'−b]=k*[x−a,y−b] x'−a=k*x−ka y'−b=ky−kb ======= x'=a+x−a*k⇔x'=k*x+a*(1−k) y'=ky+b−k*b⇔y'=ky+b*(1−k)

Eta: S(a,b) k≠0 x^'=k(x−a)+a y^'=k(y−b)+b

Mila: Mam błąd w x'. x'=a+k*x−ka x'=k*x+a*(1−k)