Planimetria + Geometria analityczna = Pakiet zadaniowy V.Abel: Mam kilka bardzo ważnych zadań, proszę o pomoc (jak da radę, to w każdym zadaniu) : 1.Wykaż, że obrazem prostej y=x w dowolnej jednokładności o środku P(0,0) jest y=x. 2.Wykaż, że prosta y=x+2 jest obrazem prostej y=x+1 w jednokładności o środku w punkcie P(0,0) i skali k=2. 3.Podstawa AB trapezu ABCD jest dwa razy dłuższa od podstawy CD. Wyznacz współrzędne wierzchołka C, jeśli A(4,−5), B(8,1), D(−3,−1). 4.(!) Prosta l₂ jest obrazem prostej l₁: x+2y−4=0 w jednokładności o środku w punkcie P(2,−1) i skali k=−2. Podaj równanie prostej l₂. // BARDZO PROSZĘ 5.Czy istnieje szceściokąt foremny o polu P=8j² i Obw=12 j ? ? ? 6. Pkt A' jest obrazem pkt A w jednokładności o środku P, a pkt B' obrazem punktu B, w tej samej jednokładności. Wyznacz pkt P i skalę, jeśli: A(1,1), A'(−1,1), B(1,4), B'(−1,8) To wszystkie zadania, naprawdę zależy mi na wytłumaczeniu lub solidnych podpowiedziach. Bardzo proszę ! ! !

Basia: ad.1 prostą wyznaczają dwa różne punkty wybieramy sobie dwa dowolne np. O(0,0) A(1,1) OO'^→ = k*OO^→ = [0;0] ⇒ O'=O = (0;0) OA'^→ = k*OA^→ = [k; k] ⇒ A'=(k,k) pr.O'A' przechodzi przez punkty (0,0) i (k;k) ma więc równanie y = ax k = a*k a = 1 czyli jest to ta sama prosta y=x ad.2 spróbuj sam w identyczny sposób ad.3 DC^→ = ¹₂AB^→ wykorzystaj to ad.4 jak (1) i (2) ad.5 Ob = 6a 6a = 12 a = 2

	a2√3		3√3a2		3√3*4
P = 6*		=		=		= 6√3
	4		2		2

jaki wniosek ? ad.6 A'B'^→ = k*AB^→ [0;7] = k*[0;3] 7 = k*3 k = ⁷₃ P(x_p;y_p) PA'^→ = k*PA^→ PA'^→ = [−1−x_p; 1−y_p] k*PA^→ = ⁷₃*[1−x_p; 1−y_p] ⁷₃(1−x_p) = −1−x_p ⁷₃(1−y_p) = 1−y_p dokończ

Mila: 4) Prosta l₂ jest obrazem prostej l₁: x+2y−4=0 w jednokładności o środku w punkcie P(2,−1) i skali k=−2. Podaj równanie prostej l₂. Jeżeli S=(a,b) środek jednokładności k− skala jednokładności to x'=kx+a*(1−k) y'=ky+b*(1−k) współrzędne punktu (x,y) po przekształceniu. a=2 , b=−1, k=−2 x'=−2x+6 y'=−2y−3 obrazem prostej l₁ będzie prosta równoległa stąd l₂: x+2y+C=0 obieram dowolny punkt należący do l₁ np.dla x=4 mamy y=0 x'=−2*4+6=−2 y'=−2*0−3=−3 Obrzaem punktu A=(4,0) jest punkt A'=(−2,−3) wstawiam do równania l₂: x+2y+C=0 aby wyznaczyć C C=8 Równanie l₂: x+2y+8=0 II sposób w programie rozszerzonym: Jeżeli S=(a,b) środek jednokładności k− skala jednokładności to x'=kx+a*(1−k) y'=ky+b*(1−k) współrzędne punktu (x,y) po przekształceniu. a=2 , b=−1, k=−2

	−1
x'=−2x+6 stąd x=		x'+3
	2

	−1		3
y'=−2y−3 y=		y'−
	2		2

podstawiamy do rownania x+2y−4=0

−1		−1		3
	x'+3+2*(		y'−		)−4=0
2		2		2

−1
	x'+3−y'−3−4=0
2

−1
	x'−y'−4=0 /*(−2)
2

x'+2y'+8=0 opuszczamy znaczki (' ) l₂: x+2y+8=0

V.Abel: Dziękuję serdecznie!.. Pytanie/ prośba o podpowiedź: Okrąg o r=1 jest wpisany w trójkąt równoramienny o podstawie równej 4. Oblicz długość ramion tego trójkąta. Mam Δ i mam ramię 2+x, i co dalej ...? // /...

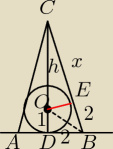
Mila: Z podobieństwa ΔCDB i ΔOEC

x		h
	=		(można inną proporcję ułożyć)
1		2

i z tw. Pitagorasa

V.Abel: Dzięki, racja, faktycznie ! ! ! Jak już kontynuuję, to jeszcze bardzo bym prosił o podpowiedź również w tym: Dłuższa podstawa trapezu ma długość 8, a krótsza 4. Oblicz długość odcinka równoległego do podstaw, dzielącego trapez na dwa mniejsze o RÓWNYCH polach.. . Bardzo proszę o pomoc, naprawdę ważne...

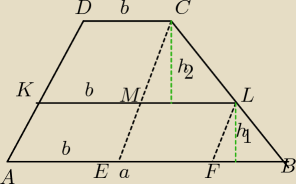
Mila: KL=e, AB=a=8, DC=b=4 Zał. P_ABLK=P_KLCD, KL II AB, CE IIAD, LF II AD

a+e		b+e
	*h1=		*h2
2		2

	a+e		h2
(1)		=
	b+e		h1

ΔFBL~ΔMLC

h2		h1
	=
e−b		a−e

h2		e−b
	=		wstawiam do (1)
h1		a−e

a+e		e−b
	=
b+e		a−e

a²−e²=e²−b² a²+b²=2e²

	a2+b2
e2=
	2

	a2+b2
e=√
	2

e=√40=2√10

V.Abel: Dziękuję ! ! ! Mila, przyjmij to jako wyrazy podziękowania

Mila:

Eta: Taki odcinek ma długość równą średniej kwadratowej długości podstaw

	a2+b2
e= √		= ......... = 2√10
	2