Napisz wzór funkcji Nowy: Napisz wzór funkcji, której wykresem jest parabola symetryczna do paraboli y = x² − 4x+2 względem podanej prostej. a)x=4 b)y=−2 c)x=−1 d)y=1 Jak sie za to zabrać ? Da sie bez rysowania wykresu ? Licze na waszą pomoc

5-latek: A czy narysowanie np. prostej x=4 i paraboli y=x²−4x+2 stanowi dla Ciebie az tak duzy problem ?

Nowy: oczywiście nie ,ale pytam czy da sie to rozwiązać bez rysowania wykresu

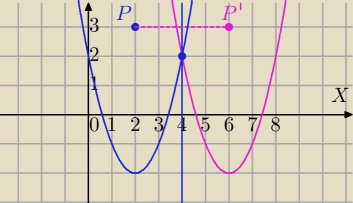
Mila: a) Ustalimy wzór przekształcenia: y = x² − 4x+2 P=(x,y) − dowolny punkt P'(x',y') − punkt symetryczny do P względem prostej x=4. Współrzędne punktu symetrycznego względem prostej x=4. P'=(x',y) S=(4,y) S jest środkiem PP'

	x+x'
4=		⇔
	2

8=x+x' Wzór przekształcenia: x'=8−x y'=y ==== Ustalamy wzór funkcji po przekształceniu: y=y' x=8−x' y'=(8−x')²−4*(8−x')+2 y'=x'²−16x'+64+4x'−32+2 y'=x'²−12x'+34 zamiana zmiennych y=x²−12x+34 szukany wzór funkcji . =========================

Mila: Ogólnie : Wzór opisujący przekształcenie płaszczyzny przez symetrię osiową względem prostej: ============ a) x=m x'=2m−x y'=y względem prostej ============ b) y=m x'=x y'=2m−y

5-latek: Dobry wieczor Milu pozdrawiam proszę spojrzeć tutaj https://matematykaszkolna.pl/forum/297365.html

5-latek: https://matematykaszkolna.pl/forum/297364.html

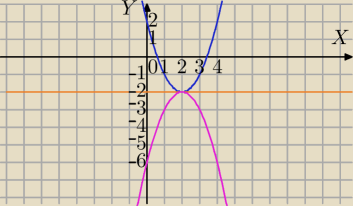
Mila: Ad (b) b)y=−2 x'=x y'=2*(−2)−y ⇔y'=−4−y stąd y=−4−y' Wzór funkcji: −4−y'=x'²−4x+2 −y'=x'²−4x'+6 /*(−1) y'=−x'²+4x'−6 y=−x²+4x−6 szukany wzór funkcji Rysunek dla sprawdzenia.

Nowy: Dzieki wielkie

Mila:

Eta: Inny sposób

	−b
a) y=x2−4x +2 xW=		= 2 , yW=f(xW)= f(2)= 4−8+2= −2
	2a

W(2,−2) W₁ jest symetryczny do W względem prostej x= 4 to W₁(2+4, −2)=(6,−2) i parabola ramionami do góry z postaci kanonicznej: y=(x−6)²−2 ⇒ y=x²−12x+34 b) podobnie W(2,−2) W ∊do prostej y= −2 i parabola ramionami do dołu to y= −(x−2)²−2 ⇒ y= −x²+4x−6 c) i d) podobnie...........

Nowy: dzięki już kilka zadań rozwiązałem tego typu dzieki za wytłumaczenie

Nowy: Przepraszam , zapomniałem dodać DZIĘKUJĘ Eta właśnie o taki sposób bez rysowania wykresu mi chodziło

AsU: Czy moge sie wtracic w punkcie b parabola po prostu sie odwróciła tak ?

J: tak

Nowy: Tak, przynajmniej tak mi sie wydaje

J: to symetryczne odbicie względem prostej: y = −2

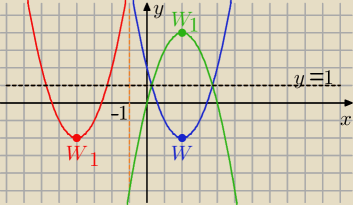
Eta: Tak jak podała ]F[Mila]] W(x,y) W₁(2m−x, y) w symetrii względem x=m i parabola ramionami tak jak pierwotna i W₁(x, 2*m−y) w symetrii względem y= m i parabola ramionami przeciwnie niż pierwotna c)W(2,−2) , W₁ symetryczny do W względem prostej x= −1 to W₁(2*(−1)−2, −2)= (−4, −2) i parabola ramionami do góry ( zwrot ramion w symetrii względem prostych x= m nie zmienia się y= (x+4)²−2 ⇒ y=x²+8x+14 d) W(2, −2) , W₁( 2,2*1 −(−2))= (2,4) parabola w symetrii względem prostych y= m ramionami do dołu to y= −(x−2)²+4 ⇒ y=−x²+4x Co potwierdzają wykresy, które narysowałam