posucha Eta: Nudy nie ma zadanek

Eta: Nie ma "krecika"?

Benny: Ktoś ukradł zadanka?

Eta: 1/ Wykaż,że iloczyn czterech kolejnych liczb całkowitych różniących się o 2 powiększony o 16 jest kwadratem liczby całkowitej .

Saizou : Zadanko dla Ety Jakie jest prawdopodobieństwo otrzymania pełnego koloru w rozdaniu brydżowym?

Janek191: Jak z trzech jednakowych sześciokątów foremnych zbudować jeden sześciokąt foremny?

Joe Black: (n−3)(n−1)(n+1)(n−3)=(n²−1)(n⁻9)=n⁴−10n²+9+16=n⁴−10n²+25=(n²−5)²

szalony: Kiedy odezwie się do mnie dziewczyna ?

Joe Black: To o coś takiego chodziło ?

Janek191: @Joe Black: Jest błąd Pewnie powinno być: ( n −3)*(n −1)*(n +1)*( n +3) = ...

Joe Black: Tak A te sześciany to na trójkąty pewnie trzeba podzielić ?

Janek191: Tam są sześciokąty, a nie sześciany

Joe Black: Miało być sześciokąty ...

Janek191: Podpowiedź Każdy mały sześciokąt dzielimy na trójkąt i pięciokąt.

Janek191: @ szalony: Pewnie musi być szalona ?

Mariusz: Eta Masz ciąg 1 2 3 4 5 6 7 8 9 10 11 12 0 1 1 2 5 6 2 3 4 0 1 4 Znajdź wzór ciągu (interpolacja nic nie daje , nie zmniejszy ilości rezerwowanej pamięci) 0 1 2 3 4 5 6 ... 25.0 25.4 25.7 26.0 26.4 26.7 27.0 ... Wzór ogólny tego drugiego ciągu jest łatwiej znaleźć

Eta: @Saizou

	4
p=		=.........
	52 13

Eta: 1/ a_n= n dla n∊N+

ZKS: Udowodnij, że dla dowolnych liczb dodatnich a ; b ; c prawdziwa jest nierówność

	1		1		1
a3 + b3 + c3 +		+		+		≥ 2(a + b + c).
	a		b		c

PW: To za łatwe: (x^3₂ − x^−1₂)² ≥ 0, czyli x³ − 2x + x⁻¹ ≥ 0

ZKS: Nie chciałem zrażać nikogo na razie. Jedyna trudność tutaj polegała właśnie na zauważeniu

	1		1
tego co napisałeś x3 − 2x +		= x(x −		)2.
	x		x

Eta:

prosta: Dla Ety : W prostokącie ABCD przekątne przecinają się w punkcie O. Punkt K jest środkiem boku BC. Odcinek DK przecina przekątną AC w punkcie M. Jaką częścią pola prostokąta ABCD jest pole czworokąta OBKM?

Mila: Oj, prosta nie wpisuj zadań dla Ety (wszystkie już rozwiązała) lecz dla maturzystów.

Eta:

prosta: dzisiaj Eta się nudzi.....a zadanko maturalne jest

Eta:

	1
Odp do zad. [OBKM]=		[ABCD]
	6

prosta: odpowiedź ok, ale skąd?

Eta: Z wiedzy,którą posiadam

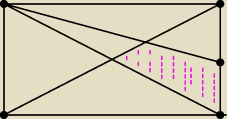
prosta: jak szybko uzasadnić, że pole tego małego trójkącika w górnym prawym rogu to 1/12 pola prostokąta

prosta: ok, jakieś trójkąty podobne i pozamiatane

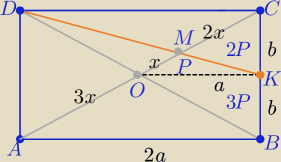
Eta: [ABCD]=24P , [BKMO]=4P

[BKMO]		1
	=
[ABCD]		6

prosta: nie widzę skąd x, 2x i 3x

Eta: https://matematykaszkolna.pl/forum/297262.html

Mila: Poprowadź linię pomocniczą z punktu B do przecięcia ze środkową ( przy tradycyjnym oznaczeniu).

Eta: Hejj Mila Do czego to doszło ....młodzi robią nam egzaminy

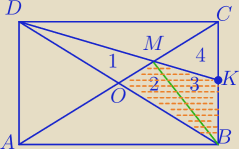
Mila: P₁=P₂=x P₃=P₄=y

	1
2x+y=x+2y=		P
	4

x=y

	1
3x=		P
	4

	1
x=		P
	12

	2		1
x+y=		P=		P
	12		6

Mila:

prosta: niektórzy mogli wcześniej pójść na emeryturkę, inni muszą do 65 dotrwać i przeżyć kolejne nowe maturki w kilku odsłonach

ZKS: To Eta możesz dać komuś takie zadanie w zamian. Udowodnić, że zachodzi nierówność

1		1		1
	+		+		≥ 4(x + y + z), gdzie liczby x ; y ; z są dodatnie
x		y		z

i spełniają warunek xy + yz + xz + 2xyz = 1.

Mila: No i jeszcze zostały ładne zadania dr Pompe. Polecam. Pozdrawiam i dobranoc

prosta: brrr...nie cierpię nierówności

Przemysław: Jak komuś się nudzi, to zapraszam https://matematykaszkolna.pl/forum/297286.html

5-latek: Dobranoc

prosta: i ja zmykam...do miłego

Eta: Kolorowych snów

Mariusz: Eta Na całki ∫R(x,√ax²+bx+c)dx działają podstawienia Eulera ale w niektórych zbiorach np u Banasia mają kaprysy i zakazują ich stosowania Masz jakiś pomysł na ominięcie podstawień Eulera (zakładamy że takie całki pojawiają się zaraz po całkach z funkcji wymiernych więc nie używamy podstawień cyklometrycznych , a funkcji hiperbolicznych i do nich odwrotnych nie znamy )

Przemysław: @ZKS Doszedłem tylko do tego, że:

1		1		1		1
	+		+		=		−2
x		y		z		xyz

No i pachnie mi coś nierównościami między średnimi. Jakaś mała podpowiedź?

ZKS: Mogę podpowiedzieć, że warunek można zapisać równoważnie jako

	x		y		z
xy + yz + xz + 2xyz = 1 ⇔		+		+		= 1.
	x + 1		y + 1		z + 1

Dodatkowa podpowiedź zastosuj odpowiednie podstawienie.

Kacper:

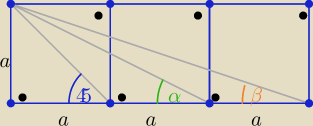
Eta: Wykaż,że α+β= 45^o

Saizou : Ja proponuję tg(α+β)=1⇒α+β=45

Eta:

	√2
lub sin(α+β)=
	2

Saizou : ale do sinusów trzeba obliczać przeciwprostokątne

Eta: łatwo je policzyć

Saizou : tangensy łatwiej

Eta: No dobrze, "uparciuszku" ........

Saizou : Dziękuję za jabłko

prosta: "prosta: nie widzę skąd x, 2x i 3x " 23.35 olśnienie: M− punkt przecięcia środkowych w trójkącie BCD Dziękuję za rozwiązania.

Przemysław: @ZKS Dzięki za podpowiedzi W ogóle, coś to mi nie wychodzi z tego:

x		y		z
	+		+		=1
x+1		y+1		z+1

mam:

1		1		1
	+		+		=2
x+1		y+1		z+1

Więc niby można zrobić tak:

1		1		1		x		y		z
	+		+		=2(		+		+		)
x+1		y+1		z+1		x+1		y+1		z+1

i dostałem:

2x−1		2y−1		2z−1
	+		+		=0
x+1		y+1		z+1

co by było bardzo przydatne, gdyby było wiadomo, że: 2x−1, 2y−1, 2z−1 jest nieujemne. Ale tego nie wiadomo można też:

1		1		1		1		1		1
	+		+		≤		+		+
x+1		y+1		z+1		x		y		z

	1		1		1
2≤		+		+
	x		y		z

Z innych rzeczy dostałem jeszcze:

	1		1		1
33≥		+		+		≥6
	x		y		z

4(x+y+z)≥6 Co tu robić:(

Mariusz: Eta 28 lipca 12:20 Ja to miałem na algebrze , trzeba było z mnożenia liczb zespolonych skorzystać

Kacper: Nic nie trzeba, ale na liczbach zespolonych w pamięci się robi

Truskawka : Mam głupie pytanie. Jest zadanie o treści: " Które wyrazy ciągu an są dodatnie jeśli a=

	n+5
	0,5 − n

Rozwiązałam: ( n + 5)( 0,5 − n) > 0 I wyszło mi, że n należy do zbioru (−∞; −5) u (0.5; +∞ ) Czyli teoretycznie wszystkie wyrazy powinny być dodatnie a w odpowiedzi jest, że wszystkie są ujemne. Co jest źle?

ZKS:

	1		1		1
Wyjaśnij mi, dlaczego		+		+		= 2?
	x + 1		y + 1		z + 1

prosta: prośba, przenieście nierówność do nowego posta

Mariusz: Kacper spamerze zawsze wiesz lepiej tyle że jak zrobiłem po waszemu to mi nie zaliczyli Poza tym po co się wtrącasz skoro cię tam nie było

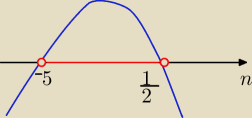
mała: @ Truskawka (n+5)(0,5−n) >0 i n∊N+ ⇒ n∊(−5;0,5) i n∊N+ −−− sprzeczność odp: wszystkie wyrazy tego ciągu są ujemne

Mariusz: ZKS ale ta równość nie zawsze jest spełniona

Janek191: @ Truskawa Źle rozwiązana nierówność n ∊ ( − 5, 0,5 )∩ ℕ⁺ = ∅

mała:

ZKS: Dobra widzę miałem zaćmienie.

	x		y
Dam kolejną podpowiedź podstawmy za		= a, tak samo		= b i
	x + 1		y + 1

z
	= c, wtedy a + b + c = 1.
z + 1

Kolejna podpowiedź. Jak nie chcesz nie patrz.

x
	= a ⇒ x = ... , tak samo z resztą i wstawić do nierówności do udowodnienia.
x + 1

mała: Mariusz ( jesteś nie miły

ZKS: Mariusz pokaż kontrargument, że nie jest ona spełniona.

ZKS: Jeżeli jest sprzeczna ta nierówność jak napisałeś, to podaj mi liczby, które nie spełniają jej skoro napisałeś to jakoś musiałeś to sobie udowodnić, że nie jest prawdziwa.

Truskawka : Mała & Janek: bardzo dziękuję nie zauważyłam, że ramiona paraboli mają iść w dół

Przemysław: @ZKS Poddaję się... Wstawiłem niby, wychodzą takie rzeczy, że nie umiem sobie poradzić:

1−a		1−b		1−c		a		b		c
	+		+		≥4(		+		+		)
a		b		c		1−a		1−b		1−c

albo w takiej postaci:

b+c		a+c		a+b		a		b		c
	+		+		≥4(		+		+		)
a		b		c		b+c		a+c		a+b

albo w takiej:

1		1		1		a		b		c
	+		+		−3≥4(		+		+		)
a		b		c		1−a		1−b		1−c

i dalej nie umiem Jak możesz to napisz proszę końcówkę rozwiązania (bo większość już napisałeś ). Widzę, że to zadanie to chyba jeszcze nie moja liga

bezendu: No to i ja mam zagadkę Jak należy ogrodzić obszar na płaszczyźnie XY przyjmując że: − wartość jednostki kwadratowej wynosi 1 dla y<20 oraz 2 dla y>20 − początek i koniec "ogrodzenia" powinien się znajdować w punkcie (0,0) − długość obwodu nie może przekroczyć 100 jednostek − wartość obszaru powinna być jak największa

ZKS: Okej doszedłeś do postaci

b + c		a + c		a + b		a		b		c
	+		+		≥ 4(		+		+		).
a		b		c		b + c		a + c		a + b

Teraz kontynuując tą nierówność doprowadzamy do postaci

b		c		a		c		a		b
	+		+		+		+		+		≥
a		a		b		b		c		c

4a		4b		4c
	+		+
b + c		a + c		a + b

dalej rozbijamy na trzy nierówności

a		a		4a
	+		≥
b		c		b + c

b		b		4b
	+		≥
a		c		a + c

c		c		4c
	+		≥		.
a		b		a + b

Dalej chyba już łatwo udowodnić te trzy nierówności.

Przemysław: Faktycznie a(b+c)²≥4abc b²+2bc+c²≥4bc (b−c)²≥0 itd. Dziękuję A jeszcze, jak to przejście:

	x		y		z
xy + yz + xz + 2xyz = 1⇔		+		+		=1
	x+1		y+1		z+1

tzn. niby jak już to mam to chyba dam radę uzasadnić, ale jak dojść z pierwszego do drugiego?

ZKS: Spróbuj zrobić od drugiego do pierwszego to wszystko zobaczysz co i jak, nie powinno być z tym za dużych problemów.

Przemysław: Znowu coś sobie nie mogę poradzić, ale: http://www.wolframalpha.com/input/?i=2xyz%2Bxy%2Bzx%2Byz%3D1%2C+x%2F%28x%2B1%29%2By%2F%28y%2B1%29%2Bz%2F%28z%2B1%29%3D%3F http://www.wolframalpha.com/input/?i=2xyz%2Bxy%2Bzx%2Byz%3Dx%2F%28x%2B1%29%2By%2F%28y%2B1%29%2Bz%2F%28z%2B1%29 co wygląda tak, jakby to jednak nie zachodziło. Może ja już zupełnie nie ogarniam

ZKS:

x		y		z
	+		+		= 1
x + 1		y + 1		z + 1

x(y + 1)(z + 1) + y(x + 1)(z + 1) + z(x + 1)(y + 1) = (x + 1)(y + 1)(z + 1) http://www.wolframalpha.com/input/?i=x%28y+%2B+1%29%28z+%2B+1%29+%2B+y%28x+%2B+1%29%28z+%2B+1%29+%2B+z%28x+%2B+1%29%28y+%2B+1%29+%3D+%28x+%2B+1%29%28y+%2B+1%29%28z+%2B+1%29

Mariusz: ZKS napisałem że nie jest prawdziwa bo patrzyłem tylko na twój wpis z 28 lipca 19:42

	x		y		z
Przy założeniu że		+		+		=1
	x+1		y+1		z+1

równość zachodzi ale równość występująca w założeniu nie jest spełniona dla każdej trójki (x,y,z)

x		y		z
	+		+		=1
x+1		y+1		z+1

x+1−1		y+1−1		z+1−1
	+		+		=1
x+1		y+1		z+1

	1		1		1
1−		+1−		+1−		=1
	x+1		y+1		z+1

	1		1		1
−		−		−		=1−3
	x+1		y+1		z+1

	1		1		1
−(		+		+		)=−2
	x+1		y+1		z+1

1		1		1
	+		+		=2
x+1		y+1		z+1