| 5 | ||
punkcie S. Wykaż że Pole czworokąta EBCS stanowi | pola prostokąta ABCD | |
| 12 |

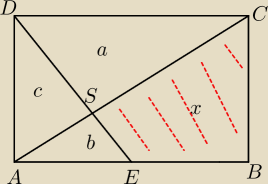 PABCD=P
PCDS=a
PAES=b
PADS=c
PEBCS=x
PABCD=P
PCDS=a
PAES=b
PADS=c
PEBCS=x
| 1 | ||
b+c= | P | |
| 4 |
| 1 | ||
a+c= | P | |
| 2 |
| 1 | ||
b= | a | |
| 4 |
| 1 | 1 | ||
a+c= | P | ||
| 4 | 4 |
| 1 | ||
a+c= | P | |
| 2 |
| 3 | 1 | ||
a= | P | ||
| 4 | 4 |
| 1 | ||
a= | P | |
| 3 |
| 1 | ||
b= | P | |
| 12 |
| 1 | ||
c= | P | |
| 6 |
| 1 | 1 | 1 | 4+1+2 | 7 | ||||||
a+b+c=( | + | + | )P= | P= | P | |||||
| 3 | 12 | 6 | 12 | 12 |
| 7 | 5 | |||
x=P−(a+b+c)=P− | P= | P | ||
| 12 | 12 |
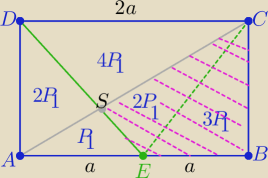 W trapezie AECD :
P(AES=P1 to P(DSC)=4*P1 i P(ASD)=P(ECS)=2*P1
oraz P(EBC)=P(AED)=2P1+P1= 3P1
P(prostokąta) = 12P1 i P(EBCS)= 5P1
W trapezie AECD :
P(AES=P1 to P(DSC)=4*P1 i P(ASD)=P(ECS)=2*P1
oraz P(EBC)=P(AED)=2P1+P1= 3P1
P(prostokąta) = 12P1 i P(EBCS)= 5P1
| P(EBCS) | 5P1 | 5 | ||||
to | = | = | ||||
| P(ABCD) | 12P1 | 12 |
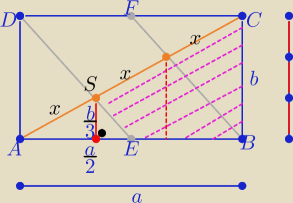 Podaję jeszcze inny sposób rozwiązania:
P(ABCD)=ab
Podaję jeszcze inny sposób rozwiązania:
P(ABCD)=ab
| ab | 1 | a | b | ab | ab | 5 | ||||||||
P(EBCS)=P(ABC)−P(AES)= | − | * | * | = | − | = | ab | |||||||
| 2 | 2 | 2 | 3 | 2 | 12 | 12 |
| 5 | ||
P(EBCS)= | P(ABCD) | |
| 12 |
 Thx
PS. Czas zdjąć rajstopy
Thx
PS. Czas zdjąć rajstopy

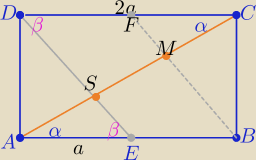 Trójkąty AES i DSC są podobne z cechy (kkk) w skali k=2
to |SC|=2|AS| to |AC|= 3|AS|= 3x , |AS|=x
analogicznie z drugiej strony : ⇒|MC|=|AS|=|MS|=x
wniosek:
Odcinki DE i BF dzielą przekątną AC na trzy równe części
stąd oznaczyłam je : x , x , x
Trójkąty AES i DSC są podobne z cechy (kkk) w skali k=2
to |SC|=2|AS| to |AC|= 3|AS|= 3x , |AS|=x
analogicznie z drugiej strony : ⇒|MC|=|AS|=|MS|=x
wniosek:
Odcinki DE i BF dzielą przekątną AC na trzy równe części
stąd oznaczyłam je : x , x , x

