F.liniowa z modułem - trudne Michał: Zbiór R jest zbiorem wartości funkcji różnowartościowej której dziedziną jest zbiór R. Ile rozwiązań ma równanie | |f(x)| −2 | = 1? Odp. uzasadnij Wyszło mi 2 Z tyłu nie ma rozwiązań Pytanie moje, 2 czy 4? Robię to tak Dla |f(x)|≥2 czyli f(x)∊(−∞,−2>∪<2,+∞) mamy |f(x)|−2=1 Czyli |f(x)|=3 czyli f(x)=−3 lub f(x)=3 Czyli stąd mamy dokładnie 2 iksy Teraz rozpatruję przedział |f(x)|<2 czyli przedział f(x)∊(−2,2) Wówczas |f(x)|−2=−1 czyli |f(x)|=1 czyli f(x)=−1 lub f(x)=1 Ani −1 ani 1 nie należą do przedziału (−2,2) Czyli 2 rozwiązania tak No dobra ale jak narysuję przykładowy wykres funkcji f(x) Potem nałożę moduł czyli |f(x)| Spuszczę o2 w doł i znowu moduł to mam np 4

5-latek: Wykres się przesuwa wzdłuż osi OX i OY a nie spuszcza Spuscic możesz ale spodnie ,

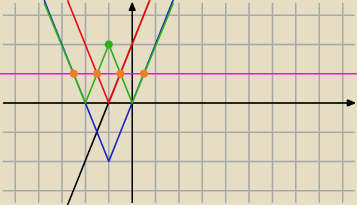
5-latek: Jeśli to jest funkcja liniowa to według mnie będą 4 rozwiązania

5-latek: ja narysowałem wykres funkcji liniowej rosnącej ale rownie dobrze możesz tez narysować wykres funkcji liniowej malejącej

Kacper: Jeśli mówimy o funkcji liniowej, to odpowiedź to 4 rozwiązania.

Michał: Czyli można postąpić tak: | |f(x)| −2 | = 1 I z tego |f(x)|−2=1 lub |f(x)|−2=−1 Czyli |f(x)|=3 lub |f(x)|=1 Pierwsze równanie wygeneruje nam dwa iksy, drugie podobnie = co nam da 4 tak? No więc nie potrzeba w rozwiązywaniu takich równań modułowych założenia że jeżeli |f(x)|−2≥0 to |f(x)|−2=1 natomiast jeżeli |f(x)|−2<0 to |f(x)|−2=−1

Michał: Odświeżam

Michał: Odświeżam

PW: Niepotrzebnie wdajemy się w jakieś rozważania o funkcjach liniowych czy monotonicznych. Założenie jest jedno: f jest różnowartościowa i zbiorem wartości jest R. Dla równania (1) |f(x)| = 3 istnieją więc dwa rozwiązania, bo funkcja f na pewno przyjmuje wartość − 3 dla pewnej x i na pewno przyjmuje wartość 3 dla innej x. To samo można stwierdzić dla równania (2) |f(x)| = 1, przy czym rozwiązania równań (1) i (2) są czterema różnymi liczbami − właśnie z powodu różnowartościowości funkcji f.

Michał: A ogólnie jest sens pisac coś takiego panie PW | |x−1| −2| = x Gdy to co jest pod modułem zewnętrznym czyli |x−1|−2 ≥0 (i to obliczamy) to |x−1|−2=x Gdy to co jest pod modułem zewnętnrzym czyli |x−1|−2<0 to |x−1|−2=−x Tak się to pisze czy po prostu bez żadnego sprawdzania i liczenia co jest pod modułem |x−1|−2=x lub |x−1|−2=−x I dodatkowe pytanie, czy już na starcie tutaj zakładamy że x>0 ?

PW: Założenie "której dziedziną jest zbiór R" mogłoby być pominięte. Ważne, że funkcja f w swojej dziedzinie D przyjmuje wszystkie wartości rzeczywiste i jest różnowartościowa.

PW: W zadaniu z 21:44 |x − 1| − 2 może być sobie jakie chce (po to piszą moduł z tego wszystkiegoi, żeby lewa strona była nieujemna). Liczba x po prawej stronie też może być sobie jaka chce, ale nie ma sensu szukać rozwiazań równania, gdy prawa strona jest ujemna. Dlatego: − w takim równaniu nic nie zakładamy o dziedzinie (jest zbiorem liczb rzeczywistych); − z powodów praktycznych w pierwszym zdaniu rozwiązania piszemy "z oczywistych powodów szukamy rozwiązań dla x ≥ 0".

Michał: Dzięki, już rozumiem. Zostały dwa zadania https://matematykaszkolna.pl/forum/294490.html https://matematykaszkolna.pl/forum/294489.html Znajdziesz tam błąd, ewentualnie dasz jakieś wskazówki/rozwiązanie