Pole powierzchni Przemysław: Jak policzyć pole powierzchni bryły? Gdybyście byli tak mili, to byłbym wdzięczny za odpowiedź

Przemysław: Nie lubicie mnie?

J: a jakiej bryły ?

Przemysław: Dowolnej.Jak wygląda postępowanie w porównaniu do obliczania objętości No to przykładowo kula albo stożek (ale bez używania tego, że to jest wykres funkcji obrócony wokół osi).

J: Dla każdej bryły jest osobny wzór.

Przemysław: Ale jak taki wzór znaleźć?

radek: stożek i ostrosłupy proste maja wzory ¹₃P podst.*wysokość, walec i graniastosłupy proste:

	4
Ppodst*wysokość, a kula:		*π*promień kuli
	3

Przemysław: Nie no, to jasne. Ale jak to wyprowadzić całkami

J: no to tu Cię boli ... też są gotowe wzory , dla brył obrotowych oraz dla brył ograniczonych powierzchniami ( całki podwójne i potrójne )

J: powierzchnię za pomocą całek liczymy tylko dla brył obrotowych

Przemysław: Właśnie nie tylko dla obrotowych. Mogą być jakieś powierzchnie przecięć albo inne cuda.

Przemysław: To gdybyście mi mogli powiedzieć − jak liczyć te powierzchnie dla brył ograniczonych powierzchniami?

Mila: Zobacz w Skoczylasie, albo Krysickim. Dział: Interpretacja geometryczna całek oznaczonych.

Mila: http://zasoby1.open.agh.edu.pl/dydaktyka/matematyka/c_analiza_matematyczna/wyklady/Wyklad23.htm Przykład − Trivial https://matematykaszkolna.pl/forum/119326.html

Przemysław: Właśnie objętości to mi się wydaje, że już trochę umiem. A w tych materiałach, co podesłałaś, jak tak tak pobieżnie spojrzałem, to nie widziałem pól, oprócz takich w |R²

Przemysław: Ale i tak dziękuję bardzo

Mila: www.au.poznan.pl/~rwal/wtd_stac_mat_pliki/wyklad₂0.doc

Mila: http://mathworld.wolfram.com/SteinmetzSolid.html

Przemysław: Hmm. Dziękuję. To już dużo pomogło

Przemysław: Mam na myśli to pierwsze, bo drugiego jeszcze nie spojrzałem.

Przemysław: Ale widzę, że to drugie też b. dobre. Dziękuję bardzo

Mila: Próbuję zrobić jakiś prosty przykład, ale odpowiedź mam inną niż w książce. Jeśli zrobię to napiszę.

Przemysław: Udało mi się stożek zrobić, teraz się męczę trochę z czym innym (przecinające się walce, już mam to rozwiązane gdzieś tutaj na forum, ale teraz jakoś inaczej chyba podchodzę)

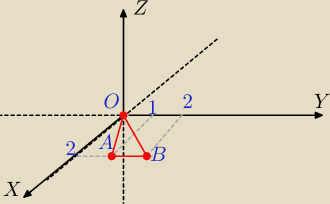
Mila: Obliczyc pole części powierzchni z=√x²−y², której rzutem na płaszczyznę Oxy jest wnętrze trójkata o wierzchołkach : O=(0,0),A=(2,1), B=(2,2). OB: y=x

	1
OA: y=		x
	2

Granice całkowania : 0≤x≤2

1
	x≤y≤x
2

f(x,y)=√x²−y² S=₀∫²[_(1/2)x∫^x (√1+f_x²+f_y²) dy]dx

	x
fx=
	√x2−y2

	−y
fy=
	√x2−y2

S=∫∫√1+(x²/(x²−y²))+(y²/(x²−y²)) dy dx=

	√2*x
=0∫2[(1/2)x∫x		dy dx= po obliczeniu całek
	√x2−y2

	2
=		π√2
	3

Przemysław: Te całki to już takie niebanalne się wydają

Przemysław: A nie, sekundę...

Przemysław: No tak, tam się poupraszczało pod pierwiastkiem sporo − dziękuję bardzo

Przemysław: A coś takiego jak tutaj: https://matematykaszkolna.pl/forum/293275.html Bo coś mieszam

Przemysław: W sensie spróbowałem dla promienia podstawy równego a. I niby coś wyszło, ale to taka duuża całka. A jak próbuję dla tego 1, to w sumie nie wiem, jak to ma być, bo przykładowo z=+− cosα i jak to potem traktować (jakoś osobno liczyć? dwa razy?)

Mila: Tam masz współrzędne biegunowe. To może jutro coś popatrzę. Nie pisałam wszystkich przekształceń, ale możesz zmienic granice całkowania najpierw po x, wtedy będzie (chyba) łatwiej. Jeśli będą kłopoty, to jutro napiszę .

Przemysław: Tak w ogóle to chyba walcowe. W każdym razie dziękuję bardzo Jutro jeszcze chyba i tak przejdę się na konsultacje to powinienem ogarnąć

Mila: Przynajmniej wiesz o co pytać, zadanie podobne do tego z 22:56 bywa na kolokwiach.