Objętość bryły ograniczonej powierzchniami gwiazda: x²+y²=1 x²+y²+z²=4 Czyli mam koło o promieniu 1 i kulę o promieniu 2, i jak mam policzyć objętość jakaś wskazówka ? Czy od kuli odjąć koło licząc całkę?

AS: Ja tak to widzę. x² + y² + z² = 4 jest sferą o środku O(0,0,0) i promieniu R = 2. x² + y² = 1 jest okręgiem o środku O(0,0) i promieniu r = 1. Okrąg jest linią,więc nie może ograniczać powierzchniowo, sądzę że powinno być x² + y² <= 1 , wtedy będzie to koło Przy tym założeniu , bryła ograniczona to walec którego podstawą jest wymienione koło a górną pokrywą część sfery położoną nad kołem.

gwiazda: Tak napisałeś , że jaki walec skąd? Właśnie nie mam odpowiedzi do tego zadania , a żadnych objętości nie miałam na ćwiczeniach.

AS: Sądzę,że należy obliczyć objętość całką podwójną i o to chodzi w zadaniu. Określić granice całkowania i przestrzeń do obliczenia.

gwiazda: No ja wiem , że całkę podwójną tylko czy mam obliczyć jako kuli minus koła czy samego koła ?

AS: Granice całkowania to: w kierunku osi Ox: −1 <= x <= 1 w kierunku osi Oy: −√1 − x² <= y <= √1 − x² w kierunku osi Oz: 0 <= z <= √4 − x² − y²

gwiazda: To wiem , ale podwójną calkę to myślam , żeby tylko zamienić na biegunowe wspołrzedne i walcowe ,i zrzutowac kule i kola na x i y ?

Trivial: x² + y² = 1 jest równaniem niezależnym od z. Jest to równanie walca nieskończonego.

gwiazda: Wiem mam walec i kulę , więc mam od walca odjać kule czy jak ?

Trivial: Chodzi im pewnie o okno Vivianiego. To jest 'walec' z krzywymi podstawami od kuli.

Trivial: Taka jakby część wspólna.

Trivial: I tu nie chodzi o całkę podwójną, gdyż całką podwójną nie liczy się objętości tylko pole. Trzeba potrójną.

gwiazda: No kulę mam walcu tylko , że kula ma większy promień od walca i na czym ta cała objętość polega ? Czyli calka potrojna z ?wiem kiepsko dziś z moim myśleniem, bo potrojne zrobiłam.

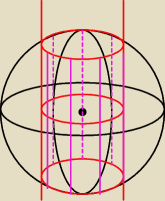
Trivial: Z tym, że góra i dół to część kuli.

gwiazda: zapisałabym to tak , że : 1≤r≤2 0≤alfa≤2π

	π		π
−		≤beta≤
	2		2

dobrze? i jak waleca objetosc mialabym policzyc tego tylko ,że wysokosc jego to 2promienie?

Trivial: Zależy o którą bryłę im chodzi. Ja stawiam jednak na to, że chodzi im o ten 'walec' w środku. W obu przypadkach stosujemy współrzędne walcowe. x = rcosφ y = rsinφ z = z. Jakobian r. Równanie sfery sprowadza się teraz do: r² + z² = 4 z = ±√4−r². Dla 'walca': 0 ≤ r ≤ 1 0 ≤ φ ≤ 2π −√4−r² ≤ z ≤ √4−r². Dla kuli bez 'walca':

4
	π*23 − (objętość walca).
3

gwiazda: Teraz wiem , ale te zadania są tak napisane , że mam takie proste nic więcej i nie wiem po czym, dokładnie jak zacząc. A odpowiedzi sa do nielicznych bo do potrojnych i podwojnych były. Dziękuję Ci ślicznie za wytrzymanie ze mną

Trivial: Czasem nie wiadomo, o którą bryłę chodzi, bo mamy ograniczone dwie lub więcej brył jak np. tu. Powodzenia na kolosie/egzaminie.

gwiazda: Egzamin wiem kiedy mam lutym, ale mam miec z 10 działow lub 12to dopiero bedzie masakra