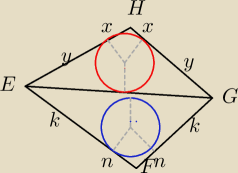
matura Kacper: Dla znudzonych językiem angielskim Dany jest czworokąt wypukly EFGH. Prowadzimy przekątną EG, następnie w każdy z trójkątów EFG i EGH wpisujemy okrąg. Wykaż, że jeśli te okręgi są styczne zewnętrznie, to w czworokąt EFGH można wpisać okrąg

Vax: Dość znany fakt Co ciekawe działa to też w drugą stronę.

Kacper: Vax ty jesteś zwolniony z matematyki z matury?

Vax: Tak.

Marek216: Łatwe ze wzoru na pole tr. P=r*p i własności czworokąta opisanego na okręgu

Kacper: To daj się wykazać tym, co piszą maturkę Z drugiej strony, to dla ciebie który fakt nie jest znany? Jakie studia jeśli można wiedzieć?

Vax: Uniwersytet Warszawski

Braun: Vax dobry wybór, ale PW też by Cię z otwartymi rękami przywitała. Zrób zadanka ode mnie co niedawno wstawiłem bo nikt nie chcę robić

Braun: https://matematykaszkolna.pl/forum/292118.html 18:24

Braun: https://matematykaszkolna.pl/forum/292058.html 11:19

YushokU: @Vax Te studia na które idą same matexy? (przepraszam, nie wiem jak się nazywa). Co do zadania, to już zaczynam nad nim myśleć.

Kacper: Dobra zadanie nr 2 W trapez równoramienny wpisano okrąg o promieniu r. Podaj mierę kąta przy podstawie trapezu, dla ktorego pole trapezu jest najmniejsze

Kacper: zadanie nr 3 Na paraboli y=4x² wyznacz punkt leżący najbliżej prostej y=x+2.

Benny: Kacper na jutro jakieś zadanka zostaw, bo dziś nie za bardzo już mi się chce myśleć

YushokU: Kurcze mam problem z tym zadaniem. Chyba mi wyszło, ale nie wiem czy ja dobrze to przyjąłem. Coś takiego mi wychodzi, tylko mi rysunek nie wyszedł jak chciałem.

Braun: 3 za proste maturę R

Blue:

	4r2
Kacper, dobrze myślę w 2, że trzeba obliczyć pochodną		?
	sinα

Kacper: zadanie nr 4 Rozwiąż równanie 2sinxcos³x−1+sin²x=0 w przedziale <0,2π>

Kacper: Braun na maturę w nowej wersji właśnie takie zadania przechodzą, bo przecież teraz jest ich około 18 w czasie 3h Blue a bez pochodnej?

Benny: 4 wydaje się w miarę krótkie

π

3π

π

3π

5π

7π

x=

, x=

, x=

, x=

, x=

, x=

?

2

2

4

4

4

4

Blue:

	π		3π		π		5π
zadanie 4:		,		,		,		?
	2		2		4		4

Benny: ojeju pomyliło mi się sin2x=1 ma okres 2π

Blue: chyba raczej π

Benny: Będzie tak jak u Blue. @Kacper a trzeba w ogóle wprowadzać ten kąt do tego zadanka? Policzyłem sobie z pochodnej bez kąta wyszedł mi kwadrat i stwierdzam, że kąt ma miarę 90^o.

Benny: Myślę co innego, piszę co innego 2π chodziło mi o sinx zwykłego

Kacper: Benny pokaż, to zobaczymy. Zadanie z równaniem poszło za szybko

YushokU: Dobra, wyszło. W zadaniu 2 wyszło mi 90 stopni, ale to musze jeszcze raz, bo coś mi nie pasuje

Benny: h=2r okrąg wpisany, więc a+b=2c z Pitagorasa wyznaczyłem a*b=4r²

	4r2
a=
	b

	4r2   +b b
P=		*2r
	2

	4r2+b2
P=		*r
	b

	4r3+b2r
P=
	b

P'(b)=b²r−4r³}{b²} b=2r, więc a=2r z czego wynika, że trapez jest kwadratem, więc kąt ma miarę 90^o

Kacper: zadanie nr 5 Liczby a,b,c z których jedna jest podzielna przez 7 tworzą ciąg arytmetyczny o różnicy równej 7. Wykaż, że liczba abc jest podzielna przez 294.

Kacper: Zadanie nr 6

	x+1
Wyznacz najmniejszą wartość funkcji f(x)=		.
	x2+x+1

Zakoduj kolejno: cyfrę jedności, cyfrę części dziesiętnych oraz cyfrę części setnych z rozwinięcia dziesiętnego wyniku.

Kacper: Zadanie nr 7

	52n
Wyznacz największy wyraz ciągu określonego wzorem an=
	n2+100

Zakoduj kolejno: cyfrę cześci dziesiętnych, cyfrę części setnych i cyfrę części tysięcznych rozwinięcia dziesiętnego otrzymanego wyniku.

Kacper: Na dzisiaj koniec Idę na debatę

Mila: Benny, ile?

Benny: Aj szkoda gadać. Po konsultacji z kolegami doszedłem do wniosku, że w zadanie z ciągiem ładnie policzyłem, wyszło mi, że a_k=a₁+10r i dałem odpowiedź, że k=10. Jak tu patrzyłem trochę na forum zdałem sobie sprawę, że zaznaczyłem, źle zadanie zamknięte, bo nie popatrzyłem na cały wykres funkcji tylko na fajne puste kropeczki

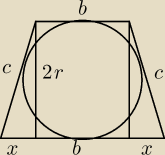
YushokU: Zad.2 bez pochodnej to będzie tak. 2b+2x=2c c²=x²+4r² P(x)=√x²+4r²*2r Funckja P(x) ma tam wartość najmniejszą gdzie f(x)=x²+4r² f(x) ma wartość najmniejszą dla x=0, gdyż jest to funkcja x² przesunięta o wektor w^→[0,4r²] dla x=0 kąt przy podstawie ma miarę 90 stopni.

YushokU: A w zadaniu 5, nie powinnno być jeszcze jakiegoś warunku, bo jeszcze nie rozwiązywałem, ale np iloczyn wyrazów ciągu {−7,0,7} wcale nie generuje liczby podzielnej przez 294

Mila: [P{Benny]], Puste kółeczko było podstępne. To górne. Zawsze podpowiadam, aby przesuwać linijkę od dołu do góry, wtedy wychwytujesz przerwę w zbiorze wartości. Tutaj była na "kawałku" dziedziny funkcja stała.

Benny: Gdybyś zobaczyła mój pośpiech w zadaniach zamkniętych... No, ale na błędach uczymy się całe życie

Mila: Przecież dobrze napisałeś, małe straty mogą być. Wszyscy byli zestresowani i potracili trochę. Przygotowuj się na piątek, może być trudne. A teraz idź spać, bo jutro piszesz angielski. Dobranoc

Benny: Właśnie chce się odbić w piątek. Jak to jest jest później liczone na studia? Podstawa + rozszerzenie? Już lecę, dobranoc

YushokU: Zależy na jakie Oby tylko mieć otwartą głowę w piątek i nie zdenerwować się zbyt bardzo to powinno być dobrze

Mila: Macie wiedzę i zimna głowa w piątek a będzie dobrze. Jutro powtórzcie to co wam , kiedys sprawiało trudność . Teraz spać. Powodzenia jutro.

Kacper: Właśnie widzę, że to zadanie jest niekompletne, ale na kserówce tak było Trzeba się zastanowić, co przydałoby się zmienić, żeby zadanko się ładnie liczyło

5-latek: Kacper Znalazlem z bibliotece pedagogicznej mysle ze fajna ksizke N. Borowikowa , E Niczyporowicz Indukcja zupelna w zadaniach

5-latek: Pisze w opisie ze jest dla nauczycieli i uczniów klas 2−4 szkoły sredniej

Kacper: Właśnie widzę, że w Warszawie jest w jednej z bibliotek, niestety daleko ode mnie

5-latek: To niech Ci sprowadzi dla Ciebie twoja biblioteka . Dla mnie sprowadza ale będę musial zaplacic 6 zl za znaczek

Lukas: Za 6 zł masz dwa piwa w ten piękny majowy czas

Metis: Albo jedno, porządne

5-latek: Lukas od niedzieli się chlodzi w lodowce Zubr . Pewnie go wypije w niedziele Metis chyba w Bibliotece pedagogicznej w Opolu maja Modenowa

Lukas: 5−latek żubr czy żubrówka bo to jest duża różnica, teraz we Wrocławiu Juwenalia wpadaj z skrzynką piwa na akademiki

5-latek: Slyszalem Godzio tez pisal

Lukas: w tamtym roku było tak https://www.youtube.com/watch?v=Pc1kpcyBjKM w tym do bani

Metis: Szkoda, 5−latku że nie ma jej na żadnej aukcji

5-latek: Niesmiertelny Time Pink Floyd dzieki ze mi przypomniales

5-latek: No nie ma

5-latek: Znalazlem jeszcze Sierpinskiego O rozkładach liczb wymiernych na ulamki proste Gosciu wystawil na allegro ale cena ....

Lukas: Sierpiński to klasyk, a rozkład na ułamki proste to banał.

5-latek: ja sobie cos przypominam ze jak mielismy wielomiany to był ten rozkład . To było potrzebne do calek . Jak obniży o polowe cene to kupie ja.

Lukas: Bez sensu, żeby nauczyc się tylko rozkładu na ułamki proste ? Miałbyś na żubra

Metis: ... kilka żubrów

Vax: @YushokU tak, te studia. @Braun, co do tych zadań co dałeś, to: 1. Wyprowadź wzór na liczbę takich podzbiorów zbioru n−elementowego, których liczba elementów jest krotnością czwórki Zauważmy, że (z dwumianu Newtona):

	n 0		n 4		n 8
(1+i)n + (1+i2)n + (1+i3)n + (1+i4)n = 4(		+		+		+ ...)

	1		1
Czyli nasza suma wynosi		((1+i)n + (1+i2)n + (1+i3)n + (1+i4)n) =		((1+i)n
	4		4

+ (1−i)ⁿ + 2ⁿ) Skąd już łatwo obliczamy: S(n) = 2^4k−2 + 2^2k−1(−1)^k , n = 4k 2^4k−1 + 2^2k−1(−1)^k , n = 4k+1 2^4k , n = 4k+2 2^4k+1 − 2^2k(−1)^k , n = 4k+3 2) Ile rozwiązań ma równanie x1 + x2 + . . . + x5 = 20 w liczbach całkowitych spełniajacych warunek: 0≤ xi ≤ 5, dla i = 1, . . . , 5? Podstawmy y_i = 5−x_i, wówczas mamy rozwiązać równanie y₁+y₂+...+y₅ = 5 dla nieujemnych y_i.

	5+5−1 5−1
Korzystamy ze znanego wzoru (można go sobie wyprowadzić) na to i wychodzi		= 126

3) Wykorzystując wielomianowy wzór Newtona, udowodnij Małe Twierdzenie Fermata, które mówi, że jeżeli p jest liczbą pierwszą, to p|(a^p − a), dla a ∈ N

	p k
Zauważmy, że p |		dla k = 1,2,3..,p−1 (istotnie, w iloczynie w mianowniku nie występuje

żaden czynnik podzielny przez p). Skąd otrzymujemy:

	p 0		p p
p | ap − a ⇔ p | (1+(a−1))p − a ⇔ p |		+		(a−1)p − a ⇔ p | (a−1)p − (a−1)

Czyli dostaliśmy tę samą tezę, tylko zamiast a mamy a−1. Możemy tak schodzić dowolnie wiele razy aż otrzymujemy równoważnie p | 1^p − 1 co jest prawdą, qed. 4) Wyznaczyć wszystkie pary (n, r), gdzie n jest liczbą cakowitą dodatnią, r zaś liczbą rzeczywistą, dla których wielomian (x + 1)ⁿ − r jest podzielny przez wielomian 2x² + 2x + 1. Popatrzmy na resztę z dzielenia x⁴ przez 2x²+2x+1, jest ona wielomianem stałym i wynosi

	1		1
−		. Stąd jeżeli n = 4k to 2x2+2x+1 | (x+1)4k − r ⇔ 2x2+2x+1 | (−		)k − r skąd
	4		4

	1
r = (−		)k
	4

W pozostałych przypadkach (n = 4k + 1, 4k+2, 4k+3) otrzymujemy w wyniku dzielenia niestałe wielomiany (co wynika z tego, że reszty z dzielenia (x+1)¹, (x+1)², (x+1)³ przez 2x²+2x+1 są niestałe), więc brak rozwiązań. Ostatecznie wszystkimi takimi parami są (n, r) = (4k,

	1
(−		)k).
	4

Braun:

Kacper: Ostatnie zadanie bardzo fajne

Vax: Oj, w rozwiązaniu 4 mała literówka Powinno być reszta z dzielenia (x+1)⁴ przez 2x²+2x+1

	1
wynosi −
	4