Ma_Tu-Ta-Lki Saizou : Wazyl specjalnie dla Ciebie usiadłem i poszperałem w książkach, żeby nie odstraszać Twoich rówieśników zad 1

	3a−b		5a+3b
Oblicz wartość wyrażenia		wiedząc że		=4
	6b		3a

zad 2 Oblicz dla jakiej wartości parametru p równanie x⁵+(1−2p)x³+(p²−1)x=0 zad 3 Na okręgu o promieniu r opisano romb, a punkty styczności są wierzchołkami czworokąta ABCD. Oblicz długość boku a rombu i długości d₁ i d₂ przekątnych rombu wiedząc że stosunek pola

	8
rombu do pola czworokąta ABCD jest równy		.
	3

zad 4 Wyznacz równanie okręgu stycznego jednocześnie do dwóch prostych o równaniach x+y−3=0 i x+y+5=0 przechodzącego przez punkt (√7,0). zad 5

	π		π		π
Rozwiąż równanie 2f'(x+		)•f'(x−		)=f'(0)−f'(2x+		) gdy f(x)=cosx
	3		6		6

zad 6 Oblicz granicę ciągu

	1   1   1   1+ + +...+   2   4   2n−1
	1   1   1   1+ + +...+   3   9   3n−1

zad 7 Uzasadnij, że dla każdej liczby całkowitej m, liczba m⁶−2m⁴+m² dzieli się przez 36. zad 8 Udowodnij że dla dowolnych liczb dodatnich a i b prawdziwa jest nierówność:

√a2+1		√b2+1		1		1
	•		≥		+		.
a		b		a		b

zad 9 Znajdź cztery liczby a,b,c,d takie, że ciąg (a,b,c) jest geometryczny a ciąg (b,c,d) jest arytmetyczny oraz a+d=21 i b+c=18. zad 10 Niech A i B będę zdarzeniami losowymi zawartymi w Ω. Wykaż że jeśli P(A)=0,7 i P(B)=0,4 to 0≤P(A∩B)≤0,4 zad 11 Dany jest ostrosłup prawidłowy trójkątny. Powierzchnia boczna tego ostrosłupa jest 4 razy większa od powierzchni podstawy. Oblicz cosinus kąta między krawędzią boczną a płaszczyzną podstawy ostrosłupa oraz cosinus kąt między ścianą boczną a płaszczyzną podstawy. 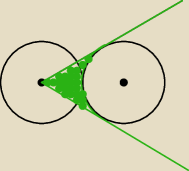zad 12 Dwa okręgi o równych promieniach są styczne zewnętrznie. Ze środka jednego z nich poprowadzono styczne d drugiego okręgu. Wykaż, że pole koła ograniczonego każdym z tych okręgów jest równe

	3Pπ
		gdzie P jest polem zacieniowanej figury. (patrz rysunek)
	3√3−π

bezendu: I jedno zadanie ode mnie, on potrafi wszystko więc to nie będzie dla niego problem

	x2dx
∫
	√−x3x−2

bezendu: poprawka w mianowniku √−x²+3x−2

Saizou : albo obliczyć granice

n		n		n
	+		+...+
n2+1		n2+22		n2+n2

Braun: To i ja dorzucę zadanie, oby się nie wystraszył i nie narobił w pampersa Wyznaczyć wszystkie pary (n, r), gdzie n jest liczbą cakowitą dodatnią, r zaś liczbą rzeczywistą, dla których wielomian (x + 1)ⁿ − r jest podzielny przez wielomian 2x² + 2x + 1.

ICSP: Nudy. Jedynie 2 ciekawe.

Braun: ICSP zachęcam Cię do mojego zadania

ICSP: Braun twoje chyba tylko jest ciekawe

Braun: To rozwiąż jak chcesz, bo Wazyl mignął na forum, ale chyba jednak pampers pełny

ICSP: Przez słowo "ciekawe" oznaczam zadania nad którymi muszę pomyśleć Rozumie, ze liczby zespolone są złym pomysłem ?

Braun: Poczekaj jest Wazyl, dajmy mu jednak czas do 22:00

Wazyl: Wyśmiewacie mnie bo napisałem że daliście za trudne zadania?

Braun: Napisałeś, że zadania były banalne. Teraz masz szansę się wykazać, to jest Twój czas Specjalnie wszystkie dla Ciebie Jak te też są banalne to poszukam trudniejszych ?

Wazyl: całka jest ok. Albo podstawienie newtona albo jakieś trygonometryczne może pójdzie podstawienie. a liczby zespolone wydają mi się dobrym pomysłem.

Vax: Nareszcie mogę robić zadania dla maturzystów:

	a		5a+3b		5t+3
1) Niech t =		, wówczas (jak łatwo widać b ≠ 0) 4 =		=		skąd t =
	b		3a		3t

	3		3a−b		3t−1		1
		, czyli		=		=
	7		6b		6		21

btw. Fajne zadanie Braun

ICSP: Vax witaj Wiesz jak pokazać taką implikacje :

	A		B
f(x) = x3 + Ax + B ∧ (		)3 + (		)2 > 0 ⇒ f(x) = 0 ma jedno rzeczywiste rozwiażanie
	3		2

Vax: Rozumiem, że ma mieć dokładnie jedno rzeczywiste rozwiązanie No to popatrzmy, kiedy tak nie jest, tj kiedy ma 3 rozwiązania rzeczywiste. Żeby tak było f(x) musi posiadać 2 ekstrema różnych znaków, liczymy, że ekstrema są w punktach x = ±√−A/3, czyli ma być

	A		B
f(√−A/3)f(−√−A/3) ≤ 0, wymnażając dostajemy (		)3 + (		)2 ≤ 0, skąd jeżeli
	3		2

	A		B
(		)3 + (		)2 > 0 f(x) istotnie ma dokładnie jedno rozwiązanie.
	3		2

ICSP: Nie wierzę, że to było takie proste Wszystko zależy od podejścia i zauważenia tego czegoś Dziękuję Ewentualnie mam jeszcze jedno zadanie gdybyś oczywiście chciał

Vax: Możesz dać, tylko teraz jestem jbc trochę zajęty bo przypominam sobie lektury ale może znajdę chwilę

ICSP: Nie ma z tym zadaniem pośpiechu Już przepisuje

ICSP: Niech n,r ∊ N. Oznaczmy przez S_r(n) sumę 1^r + 2^r + ... + n^r. Pokazać, że bez względu na wybór n oraz r zachodzi wzór :

	r + 1 1		r + 1 r
(n + 1)r − (n+1) =		Sr(n) + ... +		S1(n)

Próbowałem tak: (Oczywiście sugerowanie się moim rozwiązaniem może być błędem) Indukcja ze względu na "n" 1^o Sprawdzenie dla n = 1 :

	r + 1 1		r + 1 r		r + 1 k
P =		Sr(1) + ...		S1(1) = ∑rk = 1		=

	r + 1 k		r + 1 0		r + 1 r + 1
= ∑r+1k = 0 [		] − [		+		]=(1 + 1)r + 1 − [1 + 1]= L

2^o Założenie:

	r + 1 1		r + 1 r
(n + 1)r − (n+1) =		Sr(n) + ... +		S1(n)

3^o Teza:

	r + 1 1		r + 1 r
(n + 2)r + 1 − (n + 2) =		Sr(n+1) + ... +		S1(n+1)

Tutaj nie mam pomysłu co dalej zrobić

Vax:

	r+1 1		r+1 2		r+1 r
Chyba coś nie tak z treścią. Np dla n=1 mamy 2r − 2 =		+		+ ... +

= 2^r+1−2

Vax: Powinno być:

	r 1		r 2		r r−1
(n+1)r − (n+1) =		Sr−1(n) +		Sr−2(n) + ... +		S1(n)

Robimy indukcję po n, dla n = 1 łatwo sprawdzić, że działa. No to zapisujemy sobie założenie i mamy pokazać, że:

	r 1		r 2		r r−1
(n+2)r − (n+2) =		Sr−1(n+1) +		Sr−2(n+1) + ... +		S1(n+1)

	n k		n n−k
Ale (korzystamy z		=		):

	r 1		r 2		r r−1
P =		S1(n+1) +		S2(n+1) + ... +		Sr−1(n+1) =

	r 1		r 2		r r−1
= (		(n+1) +		(n+1)2 + ... +		(n+1)r−1)

	r 1		r 2		r r−1
+		S1(n) +		S2(n) + ... +		Sr−1(n) =

( ((n+1)+1)^r − (n+1)^r − 1) + (n+1)^r−(n+1) = (n+2)^r − (n+2) = L

	r i		r i		r i
(Po prostu dla każdego ,,i" robię		Si(n+1) =		(n+1)i +		Si(n), dzięki

czemu dostaję dwie sumy, z których jedna jest podobna do (n+2)^r = ((n+1) + 1)^r po rozwinięciu z dwumianu Newtona (jest to ta suma bez skrajnych składników), a druga jest naszym założeniem indukcyjnym)

ICSP: Dzięki

Benny: @Saizou, zadanie 2 na pewno jest w całości? Dla p∊R zawsze będzie rozwiązanie x=0

Saizou : poprawka zadania 2 Oblicz dla jakiej wartości parametru p równanie x⁵+(1−2p)x³+(p²−1)x=0 ma pięć różnych pierwiastków Dzięki za uwagę Benny

Kacper: To w taki razie zadanko łatwe

Saizou : Kacper w końcu rówieśnicy Wazyla nie mogą zejść na zawał tu na forum

Benny:

	5
Hmm w zadaniu 2 wyszło mi p∊(1;		)
	4

Saizou :