Blue Blue: Macie może jakieś podchwytliwe zadania maturalne? Chodzi mi o coś w tym stylu, jak to zadanie z układaniem klocków udostępnione przez CKE..

Alabastrowy kaszkiet: Jakie zadanie z ukladaniem klockow?

Alabastrowy kaszkiet: Napisz jak bedziesz bo jestem ciekawy jakie to podchwytliwe zadanie bylo

Ja: dostajesz na maturze klocki lego i ukladasz. Tak wyglada nowa podstawa programowa z matmy.

Martiminiano: Zadanie 33.: http://www.cke.edu.pl/images/_EGZAMIN_MATURALNY_OD_2015/Przykladowe_arkusze/2015/matematyka_PP/matematyka_PP_A1.pdf

YushokU: a czerwiec i maj 2014 już przerobiłaś? Ja teraz robię informator+zbiór zadań od CKE. A informator jest o tyle ciekawy, że są w nim(!) zadania ze zbiorków przygotowywujących do OM

Benny: Podasz linka do tego informatora?

Blue: Martiminiano, już podał, tzn. do przykładowego arkusza.. Jeśli dadzą taką maturę to coś wyczuwam duży procent tych, którzy nie zdadzą YushokU, jakie zadania masz na myśli, możesz podać konkretnie? O, czerwiec sobie przerobię, zapomniałam o tym A tak nawiasem Wam powiem, że jak dla mnie to ta nasza nowa matura jest zrobiona tak, że niewiele trudniejsze jest rozszerzenie od podstawy (jeśli ktoś oczywiście zna zagadnienia z rozszerzenia)

Martiminiano: Blue, a rozwiązywałaś matury próbne z WSiPu? Ja kupiłem od nich repetytorium i online jest dostęp do 5 arkuszy.

Blue: tylko jedną pisałam w szkole... dasz linka

Mila: Blue, masz może adres do schematu rozwiązań , do Lubelska próba przed maturą 25 luty 2015. Chcę wydrukowac dla ucznia nie moge znaleźć.

Blue: Nie, szukałam kiedyś tej matury i nie mogłam jej znaleźć ...

Mila: Maturę mam, ale chciałam dac uczniowi ze schematem. Dostanie jutro, jak rozwiążę. Rozwiąż te dwie maturki. Zaraz podam adres.

Blue: ok

Mila: http://www.zadania.info/d1631/90288 http://www.zadania.info/d1631/87249

Blue: Mila, zajrzyj tutaj: https://matematykaszkolna.pl/forum/291796.html Dziękuję, spróbuję rozwiązać dziś, a jak nie zdążę, to jutro

Blue: łee, jak są na zadania info, to odpowiedzi będą, wystarczy SMSa wysłać

52: 14. Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy ostrosłupa jest równa 12, krawędź boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 60^o. a. Wyznacz pole przekroju ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do niej pod kątem o mierze 30^o. b. Wyznacz cosinus kąta ściany bocznej przy podstawie tego ostrosłupa. c. Wyznacz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. d. Wyznacz tangens kąta dwuściennego między ścianami bocznymi tego ostrosłupa. Jak zrobisz takie zadanie, to raczej geometrię w przestrzeni umiesz P.S nie mam odpowiedzi, ale pewnie jest gdzieś to zadanie w necie albo ktoś z forum ci pomoże...

Blue: 52, dzięki, zaraz się za nie wezmę, tylko skończę obiad

YushokU: http://www.cke.edu.pl/images/_EGZAMIN_MATURALNY_OD_2015/Materialy/Zbi%C3%B3r_zada%C5%84_z_matematyki_2.pdf Geometria cz.3 I te Dodatki zadań. http://www.cke.edu.pl/images/_EGZAMIN_MATURALNY_OD_2015/Materialy/zbior_zadan_maturalnych_z_matematyki.pdf A z tego zamierzam zrobić te wszystkie R'ki.

Blue: Wrzucam moje odpowiedzi 52: a) P=54

	√3
b)
	4

	2√39
c)
	13

	12
d)
	5

Potwierdzi ktoś

YushokU: @Mila http://tinyurl.com/orn2e6e

Blue: Michał, a te zbiory są inne bo kiedyś robiłam ten drugi, popatrzyłam w ten 1 i dodatek jest chyba ten sam, ale ogólnie są tam też inne zadania?

YushokU: nie wiem, robie pierwszy, ale przeleciałem i faktycznie chyba część(albo wszystkie) się powtarzają. Są inne, np. 3cz. Geometrii, nie wiem czy robilaś.

monn: https://matematykaszkolna.pl/forum/291602.html

Blue: No to w takim razie muszę ten 1 jeszcze przerobić, może zdążę do wtorku

YushokU: A odpowiedzi mi wyszły takie same jak Tobie, chociaż wątpię, że coś tak prostego trafi się na maturze.

Blue: Mówisz o zadaniu 52?

Blue: Ja już się boję tej matury, dziś oglądałam jakąś wypowiedź gościa, który twierdził, że matura 2014 miała być tylko namiastką 2015 i że nasza niby ma być trudniejsza.... Tzn o zadaniu, które wrzucił 52

YushokU: Też tak myśle ze będzie jak te z zadania.info. Nie chce żeby taka była,ale myśle ze niestety będzie. Chociaż z drugiej strony to fajnie ze trzeba będzie sie bardziej przyłożyć do matmy żeby wyjść z dobrym wynikiem

Mila: YushokU, dziękuję .

Blue: Teraz to już się przyłożyć nie da, zostało kilka dni xD

Martiminiano: Blue, trzeba być zalogowanym żeby rozwiązywać te arkusze, a sam zrobiłem dopiero jeden i właśnie się za nie zabieram. Jeśli będziesz zainteresowana, to mogę w niedzielę udostępnić Ci moje konto.

Martiminiano: Chyba, że będziesz korzystać do godziny 20, to mogę zrobić to już dzisiaj.

Ja: Z racji na kolesi z technikum ktorzy pisza jeszcze z stara podstawa programowa to poziom trudnosci bedzie podobny(ewentualnie troche wyzszy niz rok temu) Tak powiedzial jeden gosc co pracuje w cke. Podwyzszenie popczeczki zacznie sie od 2016

Blue: Marcin, dziękuję, ale chyba sobie odpuszczę te arkusze Mam pare wydrukowanych z zadania.info, 4 zestawy z NE, zbiór od CKE i jeszcze jakieś arkusze z grupy z fejsa, więc pewnie i tak się nie wyrobię "Ja", a co mają z tym wspólnego kolesie z technikum? Bo nie ogarniam...

Blue: Czytam streszczenie i mi co chwilę myśli uciekają, wrrr Chyba czas spać

Prezesik: Blue 'Kolesie z technikum' mają w tym roku ostatnią starą mature, pewnie o to mu chodziło

Martiminiano: Czytasz szczegółowe?

Martiminiano: Mogę Ci wysłać 3−4 zadania z tego arkusza, który teraz skończyłem rozwiązywać z WSiPu. Jak dla mnie trochę przesadzili. Jak będziesz zainteresowana, to napisz i wyślę Ci na pocztę.

Kacper: Matura jest taka łatwa

Benny: @Martiminiano też bym poprosił @Kacper, dodałeś kiedyś dwa zadanka i cisza. Kiedy coś znowu wrzucisz?

Martiminiano: Benny, napisz swój adres email. Wieczorem Wam wyślę. Mnie one przerosły

Blue: Kacper, chyba dla ciebie Marcin, a prześlij, ale pewnie się załamię, jak pisałam ją w październiku to miałam marne 37%, oni przesadzają

Ja: Jakie arkusze? mi tez wyslijcie

Blue: a tak nawiasem mówiąc : czy nierówności między średnią arytmetyczną i geometryczną i arytmetyczną i kwadratową mogą się w ogóle przydać do czegoś na maturce?

Rupi: Mogą się przydać do dowodów z wyrażeń algebraicznych.

Martiminiano: Ja, to będą tylko wybrane 3−4 zadania z arkusza. Reszta była banalna, ale te które wyślę mnie osobiście przerosły Napiszcie swoje adresy email, albo napiszcie do mnie na pocztę mario2301@interia.eu ,zadania o 21 na pewno będziecie mieli na poczcie. Ogólnie zauważyłem, że zadania za 1 pkt są przeważnie bardzo łatwe, ale wśród nich zawsze trafia się jedno dosyć trudne. Te z kodowaną odpowiedzią są zawsze najłatwiejsze w całym arkuszu, później są zadania za 3 pkt, których osobiście bardzo nie lubię , a te najwyżej punktowane są takie, że albo się robi bez problemu, albo zwyczajnie nawet nie wie się jak zacząć

Blue: Bo przeglądam ten zbiór i tam są takie zadania na dowodzenie, w których niektóre byłoby chyba trudno bez tej nierówności rozwiązać

Rupi: Macie jakiś sposób jak radzić sobie z planimetrią.... ten dział mnie przerasta

Blue: Mila, strasznie proste to Lubelskie rozszerzenie

Blue: Zaraz wrzucę ten dowód z planimetrii, żeby się upewnić, czy dobrze go mam (normalnie jeden z nielicznych dowodów na rozszerzeniu, który zrobiłam )

Mila: To oznacza, że masz obiecujący poziom wiedzy.

Blue: http://i58.tinypic.com/2v333hd.jpg

Blue: łee tam, po prostu schematyczna była ^^

Blue: Ktoś sprawdzi?

Martiminiano: Przesłałem Wam 5 zadań. Odpowiedzi prześlę za jakąś godzinę.

Martiminiano: Resztę zrobiłem bez żadnego problemu, więc też dalibyście radę

Benny: Blue, w szkole jak pisałem to też tak pomyślałem. Po oddaniu przez nauczycielkę zdziwienie. Zadanko z kulami bodajże 0 pkt. Nie doczytałem czy coś tam już nie pamiętam, policzyłem prawdopodobieństwo dla innego koloru na dodatek w kluczu popełnili ten sam błąd, bo wynik był taki sam jak mój

tyu: dla chętnych Dla jakich wartości parametru m układ równań

⎧	mx−4y=tg10*tg80+m
⎩	2x+2my=−sin210−sin2100

jest spełniony przez parę liczb x, y taką, dla której x>0 i y <0 Odpowiedź to m∊(1;+∞)

Martiminiano: Było jeszcze fajne zadanie z optymalizacji w tej maturze z WSiPu, ale ono już gdzieś na pewno się pojawiło, więc Wam nie wysyłałem. Z trapezem wpisanym w okrąg o danym promieniu w taki sposób, że podstawa trapezu jest średnicą okręgu.

YushokU: @blue 90% nierówności algebraicznych które sie pojawiają na maturze to tak naprawdę sa nierówności miedzy średnia arytmetyczna a geometryczną, tylko trzeba umieć zauważyć @martiminiano Mógłbyś mi tez przesłać? Mogę sie odwdzięczyć arkuszami od Operonu z repetytorium Napisałem maila

Martiminiano: Wysłałem Jest nawet u nich schemat oceniania, więc później go prześlę

Blue: Marcin, dzięki Benny, ale ja sprawdzałam odpowiedzi z zadania.info A to jedno Wam dałam do sprawdzenia, bo na tej stronce były trochę inne oznaczenia

YushokU: @rupi Przerób dokładnie zadania z informatora CKE od Pana Guzickiego. Otwiera oczy I pamiętaj, żeby na maturze szukać tego w zadaniu co jest w tablicach Planimetria mnie na początku denerwowała i nie miałem na nią sił, ale do tego działu na prawdę potrzeba czasu, a potem sie okazuje ze jest łatwa i prosta mimo, ze nie zawsze wszystko ładnie widać Jak nie estes tegorocznym maturzystą to weź sie za kiełbasę z tego działu.

Martiminiano: Jeśli chodzi o dowody, to ja polecam książkę "Dlaczego? Zbiór zadań na dowodzenie" z Nowej Ery

YushokU: do 21:13

	sin10*sin80		1		1
tg10*tg80=		=U{−		(cos90−cos70)}{		(cos90+
	cos10cos80		2		2

	cos70
cos70}=		=1
	cos70

−sin²10−sin²100=−1+cos²10−1+cos²100=sin²(90+10)+cos²100−2=1−2=−1 czyli mx−4y−m=1 2x+2my=−1 dodajemy stronami mx+2x−4y+2my−m=0 x(m+2)+y(2m−4)−m=0 No a dalej to już klasycznie. @Martiminiano hmmm... jeśli taka będzie matura jak te zadania co przesłałeś to może dla mnie się zaczynać za 368dni, a nie za 3

Martiminiano: Jak dla mnie te 5 zadań to kosmos. Pozostałe w arkuszu były banalne, do zrobienia maksymalnie w godzinę, ale z tymi pięcioma przegięli. Tyle, że jak stracę 21 punktów 8 maja, to nie mam czego szukać...

Benny:

	1
Wykaż, że równanie cos6x*sin6x=		nie ma rozwiązań. Co myślicie o takim rozwiązaniu.
	60

	1		1
(sinx*cosx)6=(		*sin2x)6=		*sin62x
	2		64

sin⁶x przyjmuje tylko wartości dodatnie, więc najmniejsza wartość jest równa 0, największa

	1
wartość, gdy sin2x jest równe 1, więc y=
	64

	1
Zwf=<0;		>
	64

1		1
	>		, więc równanie nie ma rozwiązań.
60		64

bezendu: Tutaj masz fajne zadanka https://matematykaszkolna.pl/forum/292027.html

YushokU: @benny tak samo to zrobiłem i moim zdaniem to jest poprawne.

Martiminiano: Prześlę Wam odpowiedzi zaraz, albo udostępnię konto, na poczcie.

Martiminiano: Wysłałem Wam dane do zalogowania, za dużo zabawy z kopiowaniem odpowiedzi. Możecie się pochwalić po sprawdzeniu jak Wam poszło

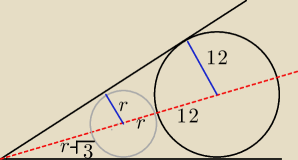
YushokU: W kąt o mierze 60stopni wpisano koła w taki sposób, że pierwsze koło ma promień 12 i jest styczne do ramion kąta, a następnie każde koło jest styczne do koła i ramion kąta. Oblicz sume pól kół. Widzimy tu Talesa. W dodatku widzimy, że środki kół leżą na dwusiecznej. tak więc:

	12
tg30=
	r+r√3+12

i otrzymujemy r=2(3−√3)² P₁=π144 P₂=π4(3−p³)⁴ Teraz obliczamy iloraz i liczymy z wzoru na sumę szeregu sumę pół kół. Dobrze? Bo coś mi skomplikowane obliczenia wychodzą, także jakby ktoś mógł sprawdzić

Martiminiano: Możesz już sprawdzić sam. Ja np. w zadaniu z prawdopodobieństwem nie zauważyłem potrzebnej zależności i wypisywałem te liczby Ale parę zjadłem

YushokU: Źle na to spojrzałem.

	12
sin30=
	12+2r+r

r=4 Więc. P₁=144π p₂=16π

	1
q=
	9

	144π
S=		=162π
	89

Ktoś potwierdzi?

YushokU: Ok, już sprawdzam maila Nic nie robiłem w tym tygodniu, bo mnie wszystko nudziło, ale widzę, że dzisiaj to sobie odrobię z tymi zadankami Bardzo dziękuję Marcin !

Benny: Też mi tyle wyszło

prosta: zaciekawiliście mnie tymi zadankami mogę też prosić o wysłanie treści zadań?

YushokU: Oblicz, ile jest siedmiocyfrowych liczb naturalnych palindromicznych (czyli takich, że są identyczne przy czytaniu w obu kierunkach, np. 6234326), w których suma wszystkich cyfr jest równa 10. _ tak na prawdę to wybieramy liczby 4 cyfrowe zacznę od tej środkowej, czyli 4 z 7 no a potem wybiorę ciągi które będą się powtarzały środkowa cyfra to 8 i mamy do dyspozycji ciągi {1,0,0} ś to 6:{1,1,0}{101}{200} ś to 4:{111}{120}{102}{300}{201}{210} ś to 2:{112}{121}{211}{220}{202}{310}{301}{400} ś to 0:{500}{401}{410}{140}{104}{311}{131}{113}{230}{203}{302}{320}{212}{221}{122} Czyli w sumie 33, to chyba wszystko. Sorry, że tu umieszczam, ale łatwiej mi będzie znaleźć błąd ewentualny, a nie chcę wchodzić na stronę wsipu, bo przy okazji zobaczę inne rozwiązania, a tego wolę uniknąć.

Martiminiano: Wysłałem.

Martiminiano: Odpowiedź w tym zadaniu to 35, więc coś "zjadłeś".

Kacper: takie zadanie wykaż że prawdziwa jest równość 1*4^1/4*16^1/16*64^1/64*...=(³₂)⁻² Powodzenia

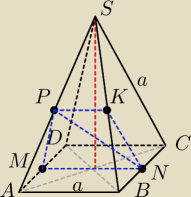
YushokU: W prawidłowym ostrosłupie czworokątnym ABCDS wszystkie krawędzie mają długość a. Na

	a
przedłużeniu krawędzi SA został wybrany punkt P, taki że AP=		. Punkty M i N są środkami
	2

krawędzi odpowiednio AD i BC. Przez punkty M, N i P poprowadzono płaszczyznę. Oblicz pole przekroju ostrosłupa tą płaszczyzną. Czyli tutaj ta płaszczyzna jak dobrze rozumiem nie będzie trójkątem jakby się mogło wydawać. MN=a

	AB		a
Z twierdzenia Talesa mamy PK=		=
	2		2

Czyli pozostało nam złapać wysokość.

	a√3
Wysokość trójkąta ABS to
	2

Wprowadzam punkt O, czyli środek podstawy i punkt F czyli środek odcinka AB i punkt G będący środkiem PK.

	a
FO=
	2

Wysokość OS obliczam z Pitagorasa i mam OS={a√2}{2} cos∡OFS=cos∡OFG=U{√3{3}

	a√3
Odcinek FG ma miarę U{a√3{2}−U{a√3{4}=
	4

Z twierdzenia cosinusów obliczam OG będące wysokością.

	a√3
OG=
	4

	3a		a√3		3a2√3
P=		*		=
	4		4		16

A tego z podzieleniem na n odcinków chyba nie umiem zrobić.

YushokU: Aha, sprawdziłem odpowiedzi. W ogóle nie dotarło do mnie to przedłużenie krawędzi, poleciałem tak jak się najczęściej zdarzało Zjadłem 2 zdarzenia. I nie zrobiłem jednego zadania. Czyli by na pewno nie starczyło Ale zadania całkiem fajne

Martiminiano: Całkiem fajne i oby 8 maja takich nie było

Martiminiano: Kacper, mógłbyś podpowiedzieć? Bo próbuję, ale coś nie mogę sobie z tym poradzić

Kacper: wsk. mamy pewien szereg

Martiminiano: Na tyle udało mi się wpaść Rozwiązuję maturę Lubelską poleconą przez Milę, ale do Twojego zadania też na pewno wrócę

Kacper: Jak byście chcieli, to mogę wstawiać zadania dla maturzystów, ale pod warunkiem, że będziecie je robić wy

5-latek: Czesc Chciałbym się przypomnieć

prosta: ten ostrosłup na rysunku...przecież punkt P leży na krawędzi AS ..nie na przedłużeniu...skoro

	a
AP=		to rysunek jest dobry
	2

kix: zadanko: Liczby a,b,c,d tworzą ciąg geometryczny. Udowodnij, że: (a²+b²+c²)(b²+c²+d²)=(ab+bc+cd)²

Vuks: za b, c, d podstawiam odpowiednio aq, aq², aq³ i wymnażam nawiasy z obu stron.

prosta: aaa może ten punkt P ma leżeć poniżej punktu A....poza krawędzią AS

5-latek: Może takie dla Blue w ramach rozrywki Zadanie : a) Sposrod n osob należy wybrać r osob a następnie z tych r osob należy wybrać k czlonkow zarządu . Pozostali utworzą komisje rewizyjna . Na ile sposobow można wybrać zarząd i komisje rewizyjna ? b) Czy liczba sposobow wyboru będzie taka sama gdy najpierw wybierze się k czlonkow zarządu a zpozostalych n−k osob wybierze się r−k czlonkow komisji rewizyjnej ? c) Sprawdz swoja hipotezę dla n=12 r=8 k=5

	n r		r k		n k		n−k r−k
d) Udowodnij wzor		*		=		*		gdzie 0≤k≤r≤n

5-latek: Jeszcze będą takie zadanka Zadanie nr 1 .

	−p
a) jaki związek zachodzi pomiędzy p i q jeśli istnieje taka liczba m ze m2=		i
	3

	q
m3=
	2

b) Udowodnij z ejezeli liczba m jest dwukrotnym pierwiastkiem wielomianu W(x)= x³+px+q to

	q2		p3
3m2+p=0 i		+		=0
	4		27

c) dla jakiej wartości q wielomian W(x) =x³−6x+q ma pierwiastek dwukrotny ? Oblicz ten pietwiastek i rozloz wielomian na czynniki Zadanie nr 2 na podstawie wykresu funkcji cosinus wyznacz dwa ciagi arytmetyczne liczb nieujennych których wyrazy spelniaja równanie

	√3
a) cosx=0,5 b) cosx=−0,5 c) cos x =
	2

Zadanie nr 3 Już dla rozluźnienia

	a1
Uczen obliczyl wartość wyrażenia		dla a=1 i q=5 i otrzymal (−0,25) jako sume
	1−q

nieskończonego ciągu geometycznego 1+5+25+... . Gdzie tkwi blad ? Może się zainteresujesz nimi . Będzie mi milo )

5-latek: ma być ciągu geometrycznego 1+5+25+125+.... .

Martiminiano: Bardzo chętnie bym te zadania wszystkie sobie porozwiązywał i się z nimi pomęczył, ale... czasu już tak mało, że lepiej chyba zrobić coś typowo maturalnego, a Waszymi zadaniami pocieszyć się po maturze W każdym razie, jeśli ktoś przespał tyle czasu co ja . Ale do zadania z szeregiem na pewno dzisiaj wrócę, Kacprze

Benny: Kacper to zadanko z Twoim szeregiem coś mi nie pasuje. Ciąg a_n=ⁿ√n jest zbieżny do 1, więc iloczyn nieskończenie wielu takich ciągów nie może być liczbą mniejsza od 1.

Martiminiano: Też nie chce mi wyjść to zadanie, a męczę się z nim i męczę

Kacper: Po prawej stronie wdał się błąd Powinno być 1*4^1/4*16^1/16*64^1/64*...=⁹√256 Przepraszam

Benny:

	n
Kurde widzę tu 4 do potęgi ( tutaj mam sumę		, ale nic nadal mi to nie daje
	4n

Kacper: Dobrze mamy taki szereg właśnie Teraz trzeba policzyć jego sumę

Benny: No i właśnie w tym jest problem. Nawet myślałem o kryterium d’Alemberta.

Blue: 5 latek, może zacznę od tego relaksu... q∊(−1,1) musi być

Blue: Ja się załamałam po przejrzeniu tej geometrii ze zbioru CKE

Kacper: Benny kryteria zbieżności szeregów pozwalają stwierdzić o ich zbieżności Nie liczą sumy

5-latek:

Benny: No i właśnie dlatego mam problem z policzeniem tej sumy. Nie wiem jak ją rozdzielić

5-latek: Straszna szkoda ze tego nie widzials wcześniej. ja to widziałem może z pol roku temu

Kacper: Benny jak do 24:00 nie dasz rady, to napiszę rozwiązanie ok?

tyu: dla chętnych wszystkie wyrazy ciągu arytmetycznego są różne od zera. Udowodnij, że jeśli jest ich co najmniej dwa, to zachodzi równość

1		1		1		n−1
	+		+ ... +		=
a1a2		a2a3		an−1an		a1an

Benny:

	4
@Kacper z		mam problem. Jakaś małą wskazówka?
	4n

Benny:

n
	*
4n

Kacper: wsk.

2		1		1
	=		+
42		16		16

Benny: Rozpisywałem tak. Kiedyś oglądałem nawet coś o tym. Było tam grupowanie wyrazów. O to chodzi?

Kacper:

Benny:

	4
Nie mogę tego znaleźć. Wnioskuje, że suma ma być równa		, ale nie mogę do tego dojść ...
	9

Kacper: Pomyśl jeszcze Obecnie nie mam czasu podać rozwiązania.

kix: Oblicz x, jeśli wiadomo, że:

	π
tgα=3x, tgβ=3−x oraz α−β=
	6

Benny:

	1
Wyszło mi x=
	2

kix: i to jest dobry wynik

Martiminiano: Moglibyście zamieścić rozwiązanie do tego zadania? Bo ja otrzymuję jakieś głupoty...

Benny:

	π
Jeśli chodzi o to z tg to α=β+
	6

	π
tg(α)=tg(β+		)
	6

zastosuj wzór na tg sumy podstawienie 3^x=t i działaj

Martiminiano: Robiłem tak, najwidoczniej pomyliłem się w obliczeniach. Dzięki.

kix:

	√3		tgα−tgβ
albo tg(α−β)=		=
	3		1+tgαtgβ

Martiminiano: Znalazłem błąd, teraz wyszło. Dziękuję

kix: Dla jakich wartości parametru p granica ciągu o wyrazie ogólnym

	pn2+2n+p
an=		jest mniejsza od p?
	(p+1)n2+pn+p

Benny: To chyba jakieś krótkie. p∊(−1;0)∪(0;+∞)

kix: z tą krótkością to mnie powaliłeś

Benny: Źle coś?

kix: jest OK

Martiminiano: O, mnie też się udało

kix: znalazłem jeszcze takie równanie: √x+1+x²−2x−1=0

tyu: wykaż, że dla dowolnych liczb a,b ∊ R zachodzi nierówność I1+abI ≤ √ 1 + a² √ 1 + b²

Kacper: Chcecie rozwiązanie tego równania?

Marek216: Wystarczy podnieść to do kwadratu i wszystko dalej powinno być jasne .

Marek216: Parę miesięcy temu cke robiło standaryzacje w mojej szkole było zadanie typu "czy kredki zmieszczą się do pudełka" i rachunek zdań, typu " udowodnij, że na j. angielski i niemiecki chodziło co najmniej ileś tam osób ". Te 2 były najwięcej punktowane. Chyba nie ma się czego bać

Kacper: Ale mnie chodziło o moje równanie (szereg).

Benny: @Kacper wrzucaj już nie chce tego, zobaczę co źle myślałem

Kacper: Po drobnych przekształceniach mamy: L=4^{1/4+2/16+3/64+4/256+...} Zajmijmy się wykładnikiem:

1		2		3		4		1		1		1		1		1		1
	+		+		+		=		+		+		+		+		+		+...
4		16		64		256		4		16		16		64		64		64

	1		1		1		1		1		1
=		+		+... +		+		+... +		+		+... + ... =
	4		16		16		64		64		256

1   4		1   64		1   256
	+		+		+ ...=
1   1−   4		1   1−   4		1   1−   4

4		1		1		1		4		1   4		4
	(		+		+		+...)=		*		=
3		4		16		256		3		1   1−   4		9

Zatem L=4^4/9=⁹√256=P c.k.d

Benny: Drugą linijkę rozpisywałem tak cały czas i nie wiedziałem jak to dalej. Zastanawia mnie zapis tej 3 linijki.

Kacper: Mamy tam sumy nieskończonych ciągów geometrycznych

Benny: Mam rozumieć, że w ciągu mamy nieskończone sumy które zaczynają się od 1/4, 1/16, 1/64 itd. i iloraz jest 1/4?

Kacper: Tak taki ciąg ciągów Wysłałem zadanka na maila.

Benny: Dzięki. Pomysł z zadaniem był dobry, ale z realizacją już trochę gorzej