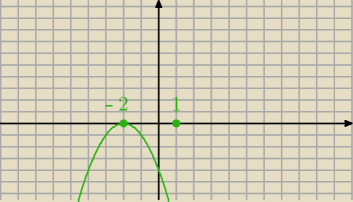
 O dzidzinie decydować będzie trójmian kwadratowy. Zauważ,że parabola jest skierowana w dół.
Jeśli Δ <0 , to trójmian bedzie przyjmował tylko wartości ujemne i funkcja nie będzie istnieć
wogóle (brak dziedziny). Jeśli jednak Δ = 0 to będzie istniał taki (jeden) x, że trójmian
będzie miał warość zero,a więc ten x bedzie należał do dziedziny. Zatem warunek jaki musimy
nałożyc na trójmian, to: Δ = 0.
Ale mamy jeszcze we funkcji √1−x . który istnieje tylko dla x ≤ 1. Zatem nasz x (miejsce
zerowe trójmianu musi być ≤ 1
Popatrz na rysunek
Reasumując, mamy dwa warunki:
1) Δ = 0
2) x0 ≤ 1
1) Δ = 0 ⇔ 4m2 − 16 = 0 ⇔ m = 2 lub m = −2
O dzidzinie decydować będzie trójmian kwadratowy. Zauważ,że parabola jest skierowana w dół.
Jeśli Δ <0 , to trójmian bedzie przyjmował tylko wartości ujemne i funkcja nie będzie istnieć
wogóle (brak dziedziny). Jeśli jednak Δ = 0 to będzie istniał taki (jeden) x, że trójmian
będzie miał warość zero,a więc ten x bedzie należał do dziedziny. Zatem warunek jaki musimy
nałożyc na trójmian, to: Δ = 0.
Ale mamy jeszcze we funkcji √1−x . który istnieje tylko dla x ≤ 1. Zatem nasz x (miejsce
zerowe trójmianu musi być ≤ 1
Popatrz na rysunek
Reasumując, mamy dwa warunki:
1) Δ = 0
2) x0 ≤ 1
1) Δ = 0 ⇔ 4m2 − 16 = 0 ⇔ m = 2 lub m = −2
| b | −2m | −2m | ||||
2) x0 = − | = | i musi być: | ≤ 1 ⇔ m ≤ 1 | |||
| 2a | −2 | −2 |
| 5 | ||
ok, dla Δ=0 rozumiem, ale jest jeszcze przypadek dla Δ>0 gdzie wychodzi m= | ||
| 2 |
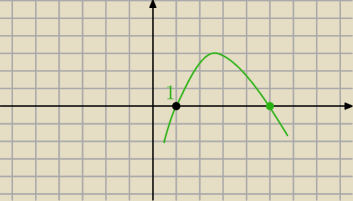 tak ...jeśli Δ > 0 , to musi być warunek: x1 = 1 , gdzie : x1 < x2 są pierwiastkami
trójmianu
wtedy dla x z przedziału (1,x2) trójmian jest dodatni , ale nie istnieje √1−x
jedynie dla x = 1 mamy dziedzinę jednoelementową
tak ...jeśli Δ > 0 , to musi być warunek: x1 = 1 , gdzie : x1 < x2 są pierwiastkami
trójmianu
wtedy dla x z przedziału (1,x2) trójmian jest dodatni , ale nie istnieje √1−x
jedynie dla x = 1 mamy dziedzinę jednoelementową