Warunki zadania Faosa: Dla jakich wartości parametru m dziedziną funkcji f(x)=√1−x − √−x²+2mx−4 jest zbiór jednoelementowy? Jakie są warunki na taki zbiór? Jakoś nmg sb tego wyobrazić...

Qulka: liczba pod pierwiastkiem ma być nieujemna czyli ≥0

J: −x² + 2mx − 4 = 0

J: Zbior jednoe.lementowy

Faosa: wiem że pod pierwiastkiem ≥0 ale to nie daje zbioru jednoelementowego;

Qulka: tak trzeba dobrać m żeby część wspólna dawała albo z drugiego Δ=0 (bo ta parabola jest smutna) albo tak żeby zaczynało się na 1 (bo pierwszy pierwiastek się na 1 kończy)

Faosa: wyszło mi m=⁵₂ i w dziedzinie x=1; Δ=0 wychodzi m =2 lub m=−2 ale przecież tymi liczbami m nie może być, bo dla jakiegoś tam x wyjdzie minus pod pierwiastkiem... chyba że wziąć pod uwagę x≥1 Jak to wgl zapisać

J: Wyrażenie pod drugim pierwiastkiem to parabola , która posiada maksimum , a więc trzeba tak dobrać parametr , aby miała maksimum w zerze. Warunek: −x² + 2mx − 4 = 0 i Δ = 0 . To ma miejsce, gdy : m = 2 lub m = − 2. Dla tych parametrów trójmian przyjmuje wartość 0 dla x = 2 , ale wtedy nie istnieje drugi pierwiastek. Wniosek: nie ma takiego m , aby dziedzina była zbiorem jednoelementowym

Faosa: dla m=−2, x=−2 więc taki zbiór chyba istnieje...

kix: dla m= −2 wyrażenie pod pierwiastkiem jest ujemne

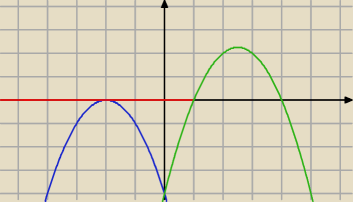
Qulka: dla m=−2 niebieska dla m=2,5 zielona

Qulka: dla m=−2 dziedziną jest x=−2 dla m=2,5 dziedziną jest x=1

kix: ups, zapomniałem o zerku