Jeżeli chcę wyznaczyć równanie prostej y=ax+b z punktu np A=(-2, -3) a wychodzi Nuwis14: Jeżeli chcę wyznaczyć równanie prostej y=ax+b z punktu np A=(−2, −3) a wychodzi mi 0=0 to co mam robić?

5-latek: Napisz porządnie tresc zadania a nie własne przemyślenia

Nuwis14: Może i masz rację. Punkt A=(−2, −3) jest wierzchołkiem rombu ABCD, którego bok zawiera sięw prostej x−3y−7=0. Punkt S=(1,1) jest środkiem symetrii tego rombu. Oblicz współrzędne pozostałych wierzchołków rombu. Napisz równanie okręgu wpisanego w ten romb

Nuwis14: Punkt C daje radę obliczyć, ale potem już mi się wszystko sypie... A zostało mi jeszcze 6 zadań

Nuwis14: Wystraszyłem?

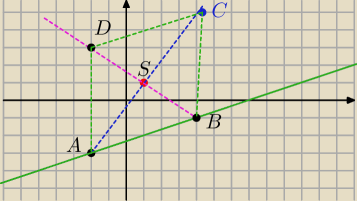
5-latek: Wiemy ze punk t przecięcia się przekątnych jest jego srodkiem symetrii Wiec Punkt S jest srodkiem przekątnej AC Ze wzoru na srodek odcina wylicz wspolrzedne punktu C Teraz cowiemy o przekątnych w rombie ? Pod jakim katem się przecinają ? Wiec napisz równanie prostej prostopadlej do prostej x−3y−7=0 (tej zielonej i przechodzącej przez S masz punkt B Wiadomo ze S jest srodkiem przekątnej DB wiec ze wzoru na srodek odcinka wylicz wspolrzedne punktu D Rysunek nie jest dokładny ale pokazuje ide rozwiązania (dokładne wspolrzedne wyznaczysz z obliczen Nad okręgiem pomysl sam

	AC*DB
Np. pole rombu P=
	2

AB to bok Obwod = 4*AB wobec tego P=p*r gdzie r− promien okręgu wpisanego w romb a p to polowa obwodu wylicz r i napisz równanie tego okręgu jego srodek już masz

5-latek: https://matematykaszkolna.pl/strona/866.html

5-latek: B− to jest punkt przecięcia się prostej rozowej z zielona

Nuwis14: no właśnie o to równanie prostej przechodzącej przez punkty A i C się na początku pytałem

Nuwis14: hmmm wiesz zapomnij o mojej ostatniej wypowiedzi. Trochę już nie kontaktuję. Zabieram się do liczenia i napiszę jak coś wyliczę

5-latek: Ide już spac ale równanie prostej przechodzącej przez dwa punkty ma postac

y−y1		y2−y1
	=
x−x1		x2−x1

Zauwaz ze prawa strona to wspolczynnik kierunkowy a tej prostej Albo tez zapoznaj się z tym https://matematykaszkolna.pl/strona/1223.html. Czesc Dobranoc

Nuwis14: Cześć. Dziękuję za pomoc

5-latek: https://matematykaszkolna.pl/strona/1223.html Oczywiście tak Można to zadanie rozwiazac tez inaczej np. za pomocą wektorow lub wykorzystując fakt ze dwa przeciwlegle boki w rombie sa rownolegle