f
kasztan: Niezależne zmienne losowe X i Y mają jednakowe funkcje prawdopodobieństwa:
xi | 0 | 1 | 2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
pi |1/3 | 1/3 | 1/3
Niech U1 = X + Y, U2 = 2X, U3 = XY, U4 = X2. Wyznacz ich funkcję prawdopodobieństwa
Pomoże ktoś, o co tu w ogóle chodzi ?
6 kwi 16:09
Qulka: i co z Tego że Ci napiszę jak i tak nie będziesz wiedział jak, a na malowanie wszystkiego od
początku w tym edytorze nie mam już siły
6 kwi 16:17
kasztan: to do tego zadania potrzebne są wykresy ?
6 kwi 16:18
Qulka: nie..tabelki

6 kwi 16:20
kasztan: trudne jest te zadanie ?
6 kwi 16:20
kasztan: a ile tych tabelek ma byc ?
6 kwi 16:20
6 kwi 16:32
Qulka: zadanie 2.58 na 113 jest podobne
na 128 masz odpowiedź analizuj

6 kwi 16:37
kasztan: ok będę próbować
6 kwi 16:40
Qulka:
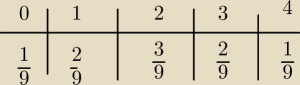
U1=X+Y
6 kwi 16:41
6 kwi 16:41
Qulka: U3=2X to taka jak masz tylko X•2
czyli 0 | 2 | 4
1/3 | 1/3 | 1/3
6 kwi 16:42
Qulka: tzn to było U2
6 kwi 16:42
kasztan: w sumie to U1 = X + y rozumiem tylko nie wiem skąd 3 i 4 się wzieła jak jest w poleceniu tylko
do 2
6 kwi 16:43
Qulka: bo X=0,1,2 Y=0,1,2
to X+Y= 0,1,2,3,4 bo dodajesz każdy z każdym
6 kwi 16:52
kasztan: jednak nie rozumiem np. dla 1 jest 2/9 a 1/3 + 1/3 to 2/3
6 kwi 16:57
Qulka:
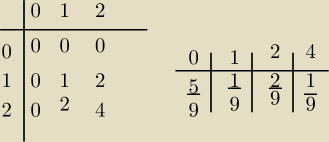
U3=X•Y
wygląda tak prosto bo wszystkie p=1/3
normalnie pi też trzeba mnożyć
6 kwi 16:59
Qulka: MNOŻYSZ pr−wa i dodajesz wszystkie przypadki... mówiłam że rozpisanie od początku to dużo
zabawy
6 kwi 17:00
Qulka: U4=X2 to taka jak masz tylko X2
czyli 0 | 1 | 4
1/3 | 1/3 | 1/3
6 kwi 17:01
6 kwi 17:02
kasztan: a dobra jest ok, bo:
6 kwi 17:06
Qulka: 
6 kwi 17:06
kasztan: to np. dla U1 = X + Y mam zapisać wszystkie wyniki niepowtarzających się tak jakby kombinacji
dodawań ?
0+0,0+1,0+2,1+1,2+2 ?
6 kwi 20:14
Qulka: tak
6 kwi 20:15
kasztan: i czemu dla 0 jest 1/9 a dla 1 jest 2/9 ? to nie jest wszędzie 1/3 + 1/3 ?
6 kwi 20:15
Qulka: to nigdzie nie jest 1/3+1/3
wszędzie jest 1/3 • 1/3 • tyle ile jest takich przypadków pasujących
6 kwi 20:16
kasztan: to np. dla 0 jest 1/9 bo jest tylko jedna kombinacja 0 + 0 , więc 1/3 * 1/3 = 1/9
dla jest też jedna kombinacja 0 + 1 to czemu jest 2/9 a nie 1/9 ?
6 kwi 20:19
kasztan: miało być dla 1*,
czy dla 1 są 2 kombinacje bo 0 + 1 i 1 + 0 , w taki sposób ?
6 kwi 20:20
Qulka: bo możesz 0+1 lub 1+0 bo raz x=1 y=0 potem x=0 y=1
6 kwi 20:20
kasztan: i w mnożeniu U3 = X * Y jest podobnie ?
bo 0 * 0, 0 * 1, 0 * 2, 1 * 0 , 2 * 0, więc 5/9 dla xi = 0 ?
6 kwi 20:25
Qulka: tak
6 kwi 20:26
kasztan: dla U4 = X2 to będzie tak:
xi 0 1 4
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
pi 1/3 1/3 1/3
6 kwi 20:27
dyskretna: Qulka, dobra jesteś z dyskretnej ? nie chcesz pomóc odpłatnie ?
6 kwi 20:28
kasztan: dobrze dla U4 podałem ?
6 kwi 22:37
daras: 
6 kwi 22:38
Qulka: U4 OK
6 kwi 22:44


 U1=X+Y
U1=X+Y
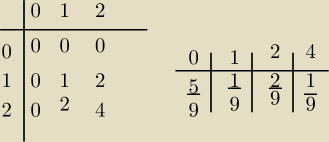 U3=X•Y
wygląda tak prosto bo wszystkie p=1/3
normalnie pi też trzeba mnożyć
U3=X•Y
wygląda tak prosto bo wszystkie p=1/3
normalnie pi też trzeba mnożyć

