sfd kasztan: Obliczyć wariancję, odchylenie standardowe, kwartyl dolny i górny, medianę i modę zmiennej losowej X o gęstości:

	1
		x2 dla 0 ≤ x ≤ 3
	9

f(x) = 0 w p.p co oznacza skrót p.p ?

Qulka: w pozostałych przypadkach

Qulka: http://home.agh.edu.pl/~adan/wyklady/rpis3.pdf

PR: Pani Qulko sprawdzi Pani ten 2 wynik co mi wyszedł ? Bardzo bym prosił https://matematykaszkolna.pl/forum/287616.html

Qulka: EX=∫x³/9 dx=x⁴/36 = 81/36 = 9/4 EX²=∫x⁴/9 dx= x⁵/45 = 27/5 DX=27/5−(9/4)²= 0,3375 mediana ∫x²/9 = x³/27 = m³/27=1/2 m_e=2,3811 kwartyl dolny q³/27=1/4 q=1,88988 górny q³/27=3/4 q=2,72568

kasztan: ską x³/9 ? jak w poleceniu jest x²/9 ?

Qulka: z definicji EX=∫ x•f(x) dx stąd jeszcze jeden x we wzorze

kasztan: przez pierwsze 3 linijki to co jest liczone ? EX to średnia ?

kasztan: i dlaczego tak mediane i kwartyle obliczasz ? to z definicji jakiejś ?

Qulka: tak

Qulka: widziałeś te linki co wkleiłam

kasztan: tak, ale ciężko mi zrozumieć te zapisy matematyczne

Qulka: to wczytaj się tylko w strony 13,14 i 15 tam jest to co Ci potrzebne

kasztan: a DX to co to w ogóle ? Bo są jakieś wzory ale nie jest napisane co to jest

kasztan: w drugiej linijce Twoich obliczeń nie powinno być E(X²)?

kasztan: pierwsze 3 linijki dotyczą liczenia wariancji ? DX to ta wariancja ?

Qulka: tak to wariancja ale powinno być D² bo tak sie to zapisuje

kasztan: a czemu jak liczysz mediane to x potem zamienia się na m?

kasztan: po co określenie w zadaniu , że 0 ≤ x ≤ 3 jak nigdzie tych liczb się nie wpisuje ? czemu w kwartylach jest q do potęgi 3?

Qulka: bo to całka od 0 do m i podstawiasz na końcu

Qulka: wpisujesz te liczby w granicach całkowania ale w tym edytorze ciężko to zgrać bo to 3 piętrowe by było

kasztan: to wszędzie będzie 3 ∫ ? 0

Qulka: ja je podstawiam na końcu działań za x (najpierw 3 a potem 0 ) tyle że tego 0 już nie pisałam

Qulka: w pierwszych dwóch potem w medianie całka od 0 do m a w kwartylach całka od 0 do q

kasztan: w kwartylach ∫x²/9 przyrównuje do 1/4 i 3/4 ? ale czemu w medianie x na m zamieniasz ?

Qulka: w medianie przyrównujesz całkę do 1/2 bo to granica całkowanie podstawiasz na końcu i to samo w kwartylach

Qulka: str 14 http://home.agh.edu.pl/~adan/wyklady/rpis3.pdf

kasztan: czyli przy liczeniu mediany będzie: m ∫ x²/9 = x³/27 (już bez tego 0 i m ?) 0 m³/27 = 1/2 2m³ = 27 / 2 m³ = 13,5 m = ³√13,5 ?

Qulka: w pierwszej linijce na końcu piszesz pionową kreskę (albo nawias kwadratowy) i tam dopisujesz m i 0 porównaj stronę 13 link

Qulka: tu masz jeszcze zebrane wzory http://antenor.pol.lublin.pl/users/gorgol/st3-druk.pdf

kasztan: m m ∫x²/9 = [x³/27] 0 tak ma być ?

Qulka: tak

Qulka: i potem od końca odejmujesz początek więc m³/27 − 0³/27= m³/27

kasztan: zaraz wrzucę całe zadanie rozwiązane, a po co te 0 w pozostałych przypadkach ? używa się kiedyś tego 0 ?

kasztan: czemu w pierwszej linijce pod x'a zostaje podstawiona liczba 3 , a nie np liczba 2 ?

Qulka: bo granicą całkowania jest od 0 do 3

kasztan: to czemu nie 0?

Qulka: wstawiasz oba bo od końca odejmujesz początek więc tak jak o 15:17 x⁴/36 ]₀³ = 3⁴/36 − 0⁴/36 = 81/36

kasztan: i tak samo się odejmuje w przypadku mediany i kwartyli ?

Qulka: tak samo odejmuje się w przypadku KAŻDEJ CAŁKI oznaczonej

kasztan: Wariancja: 3 3

	x3		x4		81		9
E(X) = ∫xf(x)dx = ∫		dx = [		]30 =		=
	9		36		36		4

0 0 3 3

	x4		x5		27
E(X2) = ∫x2f(x)dx = ∫		dx = [		]30 =
	9		45		5

0 0

	27
D2(X) =		− (9/4)2 = 0,3375
	5

Odchylenie std. δ = √0,3375 − tak to oznaczyć ? Mediana: m

	1
∫f(x)dx =
	2

0 m

	x2
∫		= [Ux3}{27}]m0
	9

0

m3		1
	=
27		2

2m³ = 27 m³ = 13,5 m_e = ³√13,5 kwartyl dolny: q

	1
∫f(x)dx =
	4

0 q

	x2		x3
∫		= [		]q0
	9		27

0

q3		1
	=
27		4

4q³ = 27 q³ = 6,75 q ³√6,75 tak samo kwartyl górny. Dobrze ?

Qulka: tak

Qulka: odchylenie std oznacz D(X) skoro wariancję oznaczyłeś D²(X)

kasztan: a jak obliczyć modę ?

Qulka: max z x²/9 więc modą jest 0

Qulka: miało być 3

kasztan: jak to max z x²/9 ? 3 podstawić pod x'a ?

Qulka: narysować wykres i zobaczyć gdzie największy w przedziale <0,3>

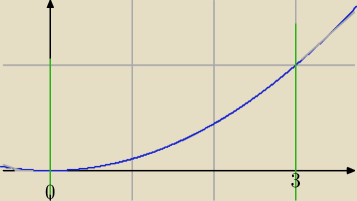
Qulka: jak widać największy jest w 3

kasztan: ok dzięki czyli wystarczy napisać że moda = 3

Qulka: tak

kasztan: ok to dzięki !

kasztan: sam bym tego nie rozwiązał

kasztan: Mam takie podobne zadanie: Zmienna losowa X posiada gęstość:

	3		45
f(x) = −		x2 + 6x −		dla x∊ <3;5>
	4		4

0 w p.p to te zadanie robi się tak samo jak powyższe ?

Qulka: tak