oblicz wymiary prostopadłościanu o największej objętości Aga: Dany jest stożek o promieniu podstawy 6 cm i wysokości 8 cm. W stożek ten wpisujemy prostopadłościany tak, że jedna podstawa zawiera się w podstawie stożka a wierzchołki drugiej podstawy należą do powierzchni bocznej stożka. Wiedząc, że stosunek długości krawędzi podstawy jest równy 3, oblicz wymiary tego prostopadłościanu, którego objętość jest największa.

PR: Czy posiadasz odp. do tego zadania? Wyszło mi 6x18x4.

PR: Oj głupi błąd Prędzej to : 3√2 x 9√2 x 4

Frost:

	8		8
Mi wyszły		x		x 8
	3		3

Aga: w odpowiedziach jest 4√10 /5 na 12√10 /5 na 8/3

Frost:

	8
Nie jest źle wysokość wyszła mi tak jak w odpowiedziach
	3

Aga: i jest jeszcze wskazówka ze V(x)=24x² − 2√10 x³ tylko nie wiem jak stworzyć tą funkcję

Qulka: oo to mam dobrze ..a już mnie ten pierwiastek martwił

PR: Teraz też mam dobrze...potraktowałem prostokąt jako kwadrat...ah te Święta

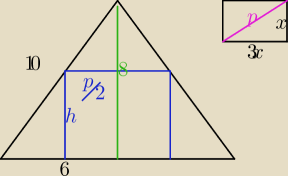
Qulka: p − przekątna podstawy =√10x (z Pitagorasa)

h		8
	=		wyliczasz
6−p/2		10

V=3x²•h

Aga: dzięki

TypowyJanusz: Skąd się bierze te p/2?

Stupid: I jeszcze jedno pytanie z czego wynika zależność, że h do 6− p/2 ma się tak jak 8 do 10?

kix: z pana Talesa

Stupid: Ok wszystko gra tylko nie pasowało mi te 8 do 10, bo powinno być 8 do 6

Qulka: Janusz z obrazka na górze obok p to przekątna podstawy tego prostopadłościanu więc do połowy jest p/2

Qulka: No tak ..powinno być 8/6

:D: Δ Δ Ω ∞

Artur: Jakby ktoś wytłumaczyłby mi skąd się bierze, że przekątna podstawy to √10x to byłbym bardzo wdzięczny

wredulus_pospolitus: masz prostokąt o bokach x i 3x ... z tw. Pitagorasa: p² = (x)² + (3x)² −> p² = 10x² −> p = √10x

Artur: Dziękuję bardzo, nie myślę ostatnio