Maturka cz.2
Benny: Czy jest możliwość rozwiązania tego zadania 8 bez tego wzoru? Bo tym sposobem nie ma opcji
żebym to rozwiązał, ponieważ nie słyszałem nigdy o tym wzorze

15 mar 00:04
Qulka: hmm.. bardzo precyzyjna i dokładna informacja

15 mar 00:43
mm:
P=πr
2 może być?

15 mar 00:44
15 mar 01:07
Qulka: czyli tam rozwiązane a tu możemy pospamować

15 mar 01:11
Benny: Zostałem poproszony o założenie nowego wątku, więc jest

15 mar 10:20
5-latek: Ale nalezalo napisac zadanie lub wskazac link
Bo u mnie w ksiazce np zadanie nr 8 jest takie
Czy wobev znalezienia w paragrafie 2 zwiazku −potrzebna jest specjaklna tablica cotangensa.
Przy pomocy zbudowanej z zadaniu nr 5 tablicy tangensow znalezc 1)ctg40, 2) ctg65 3) ctg75

15 mar 12:51
Benny: To dziś co robimy?

15 mar 12:54
5-latek: To z czego chcesz zadanka ?
15 mar 12:57
Qulka: mam kilka nierozwiązanych całek i jedno równanie różniczkowe

15 mar 12:59
Benny: A obojętnie

Ostatnio coś pisałeś, że dołożysz jakieś zadanka z ciągów, pochodnych i
planimetrii. Dawno nie rozwiązywałem zadanek od
Mili 
15 mar 12:59
Benny: Musiałbym przestudiować trochę całki i równania różniczkowe. Tak się składa, że wypożyczyłem
ostatnio Analizę matematyczną to może coś tam bym znalazł

15 mar 13:01
5-latek: Dzien dobry
Aniu
Dawaj sprobuje . najwyzej pojade do dr. Gewerta albo Skolczylasa . Niech rozwiazuja . A co mi
to

Tak powaznie to jeszce nie teraz
15 mar 13:03
15 mar 13:06
15 mar 13:07
5-latek: Napiszse CI kilka zadan z ciagow
Zadanie nr 1
Boki a,b , c, i wysokosc h opuszczona na bok a tworza ciag geometryczny . Udowodnic ze ten
trojkat jest prostokatny .
Zadanie nr 2
Wykazac ze jezeli liczby a
1,a
2, a
n(dodatnie tworza ciag geometryczny to a
1 a
2
a
n=(a
1a
n)
1/2n
Zadanie nr 3
Wykazac ze dla dowolnych liczb a
1,a
2,a
3(roznych od zera takich ze liczby a
13,a
23 a
33
tworza ciag arytmetyczny spelnina jest rownosc
| 1 | | 1 | | 2 | |
| + |
| = |
| |
| a12+a1a2+a22 | | a22+a2a3+a32 | | a12+a1a3+a32 | |
Zadanie nr 4
Logarytmy trzech liczb tworza ciag arytmetyczny . Suma odwrotnosci tych liczb =39, a suma
kwadratow odwrotnosci =819 . Znajdz te liczby .
Zadanie nr 5
| | an2−1 | |
dany jest ciag o n−tym wyrazie bn= |
| |
| | (a−1)n2+n | |
Wyznacz yc wartosc parametru a tak aby granica tego ciagu byla liczba 2 . czy dla znalezionej
wartosci a otrzymany ciag jest rosnacy
Zadanie nr6
| | 9 | |
W nieskonczonym ciagu geometrycznym ktorego suma = |
| piwrszy wyraz jest rowny √x−2 a |
| | 2 | |
trzeci jest odwrotnoscia pierwszego . Wyznacz x
Zadanie nr 7
| | 1 | |
Dla jakich t zbiezny jest ciag [(2cost)n+ |
| ]? |
| | (1=sin2t)n | |
Znalezc dla jakich wartosci x ciag a
n=(tgx)
2n jest rosnacy .
Tyle moze wystrczy .
15 mar 13:29
Qulka: wrocławskie są ładniejsze

15 mar 13:30
5-latek: W nr7 ma byc(1+sin2t)n
15 mar 13:31
5-latek: dziekuje CI za linka

Juz sobie go zapisuje
15 mar 13:33
Benny: Nr 1
ciąg a,b,c,h jest geometryczny, więc:
b
2=a*c
c
2=b*h
Jeśli w trójkącie prostokątnym oznaczymy b i c jako przyprostokątne i a jako przeciw
prostokątna
to b*c=a*h
a
b
2=a*c
c
2=b*h
a*h
2=c
3
a*h=b*c c.n.w
15 mar 13:40
Benny: W tym drugim nie za bardzo rozumiem zapis
15 mar 13:44
5-latek: Napiszse jeszcze raz
Wykazac ze jezeli liczby dodatnie a1,a2,.......an tworza ciag geometryczny to a1 a2
....... an=(a1an)n/2
Wedlug mnie to po slowie (to) bedzie iloczyn tych liczb
15 mar 13:59
5-latek: Ale tez rozwiaz sobie te zdania ktore w linku podala Qulka . Sa bardzo ciekawe
15 mar 14:01
Benny: Zad nr 5 a=2, różnica bn+1 − bn=2n−2 więc ciąg jest rosnący
15 mar 14:01
5-latek: | | 2 | |
a=2 ale bn+1−bn= |
| to jaki to bedzie ciag ? |
| | n(n+2) | |
15 mar 14:06
Benny: zad nr 6 x=4,25 lub x=11
15 mar 14:24
Benny: aj tam miało być 2n+2
mianownik pominąłem, bo jest zawsze dodatni, no i oczywiście teraz sobie mogłem skrócić tak jak
Ty, ale ciąg i tak będzie rosnący

15 mar 14:28
5-latek: | | 1 | |
Tak to bedzie gdy q= |
| |
| | √x−2 | |
| | 1 | |
ale tez iloraz q moze rownac sie q=− |
| i q∊(−1,1) wiec wyliczc z tego x tez |
| | √x−2 | |
15 mar 14:36
Benny: a to zadanko nr 1?
15 mar 14:46
5-latek: Skoncz liczyc to zadanie nr 6
Napisz jaki wyszsedl CI pierwiastek dla tego q
15 mar 14:49
5-latek: Powiem CI ze bardzo ladny wyjdzie (az przyjemnie na niego popatrzc

15 mar 15:04
Mila:
Benny, jaki cel chcesz osiągnąć, podaj, to ułożę zestaw.
15 mar 15:09
Benny: No teraz mam jeszcze tydzień, żeby do diamentowego indeksu się przygotować, więc może coś pod
to?
15 mar 15:21
Benny: | | 133−√12393 | | 133+√12393 | |
Wyszło mi x1= |
| i x2= |
| z czego x1∉D |
| | 8 | | 8 | |
15 mar 15:25
5-latek: | | (133+9√153) | |
ja mam taki |
| wiec to samo i gitara |
| | 8 | |
15 mar 15:44
5-latek:
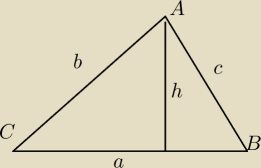
Nr1 .
W zwiazku z tym ze a,b,c, i h tworza ciag geometryczny to a:b=c:h
wiec a*h= b*c
Ale wiemy ze a*h to podwojona wartosc pola trojkata ABC (tak ?
Wiemy tez ze 2P= b*c*sin CAB(tez wiadomo
wiec wobec rownosci a*h=b*c mozemy zapisac ze b*c*sinCAB=b*c to sin CAB=1 to
CAB=90
o (czyli trojką prostokątny
15 mar 15:57
Benny: To co z tym pierwszym?

15 mar 15:58
5-latek: Masz wyzej

15 mar 15:58
Benny: Nie odświeżyłem i nie zauważyłem Twojego posta. Wobec tego co Ty wysłałeś moje rozwiązanie
można uznać?
15 mar 16:00
5-latek: Ja bym powiedzial tak Cale Twoje + to moje i jest OK
15 mar 16:04
5-latek: Jak Ty sie na to zapatrujesz ?
15 mar 16:09
Benny: Wydaję się ok

15 mar 16:14
Mila:
1) Wyznacz równanie zbioru środków wszystkich okręgów stycznych zewnętrznie do okręgu:
x2+(y−3)2=16 i do prostej y=−1.
Podaj interpretację geometryczną rozwiązania.
2) Znaleźć wszystkie wartości parametru p, dla ktorych równanie:
(p−1)*4x−4*2x+(p+2)=0 ma przynajmnie jedno rozwiązanie.
3)Dla jakich wartości parametru m pierwiastki równania
(m+1)x2−2x+m−1=0 należą do przedziału (0,2).
15 mar 16:14
5-latek: Teraz zajmij sie zadaniami od
Mili 
Pozdrawiam .
Potem jesli bedziesz chcial to wrocisz do moich OK?
15 mar 16:17
Benny: Jasne

15 mar 18:17
Benny:
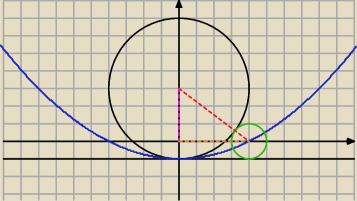
|
AB|
2=|
BC|
2 + |
CA|
2
|AB|=r
1+r
2
|BC|=3−y
|CA|=x
|AB|=4−y+1−5=5−y
(5−y)
2=x
2+(3−y)
2
Do tego zadanka mam takie małe pytanko. Jeżeli w poleceniu mamy "Wyznacz równanie zbioru
środków wszystkich okręgów" to liczy się tylko ta parabola? Bo po samym narysowaniu okręgu i
prostej możemy stwierdzić, że prosta jest styczna do okręgu, więc drugi okrąg będzie leżał po
drugiej stronie prostej.
15 mar 19:46
Mila:
Odp.
| | 1 | |
Środki okręgów leżą na paraboli y= |
| x2−1 gdy y≥−1 oraz na pólprostej x=0 gdy y<−1. |
| | 16 | |
15 mar 20:21
Benny: Czyli dobrze myślałem

15 mar 20:23
Benny: Milu w tym zadanku nr 3 trzeba rozwiązać taki układ:
a≠0
Δ≥0
0<x1<2
0<x2<2
i może jeszcze −b/a>0, c/a>0 czy tego już nie trzeba? Czy może jakiś inny sposób z tymi
pierwiastkami?
15 mar 22:31
Mila:
1) sprawdź dla m=−1
2) Δ≥0 , sprawdź, gdy Δ=0
i koniunkcja nierówności wystarczy.
odp.(m∊(1,√2>
15 mar 22:58
Benny: Podpunkt 1) oczywisty, sprawdziłem na samym początku

no a co z tym przedziałem (0;2)?
15 mar 23:00
Mila:
Albo nierówności ( męczące)
albo
xw∊(0,2) i jeśli m+1>0 to f(0) >0 i f(2)>0
jesli m+1<0, to f(0)<0 i f(2)<0
15 mar 23:11
Benny: Ok, przeanalizuje to jeszcze jutro. Jak możesz to dopisz jakieś zadanko, rozwiąże w szkole.
Dobranoc

15 mar 23:21
Mila:
Było kiedyś podobne na "Indeksie". Dość trudne.
4)Wykaż, że 30 początkowych wyrazów ciągu (,33,333,3333,....) nalezy do przedziału :
(1029,1030)
15 mar 23:30
Mila:
(3,33,333,3333,....)
15 mar 23:37
16 mar 16:38
Benny: Więc tak zadanie 2) p∊(−2;2>/{1}
16 mar 16:48
Benny: W tym 4 chodzi o sumę, tak?
16 mar 16:49
Benny: | | 1 | | 280 | |
w 4 suma wyszła mi |
| *1030 − |
| co oczywiście należy do danego przedziału  |
| | 3 | | 3 | |
16 mar 20:47
Benny: Milu jesteś?
16 mar 21:56
Mila:
2) Mam inny wynik, przeliczę.
4) Oczywiście , masz rację, przepraszam.
Wykaż, że
suma 30 początkowych wyrazów ciągu (3,33,333,3333,....) nalezy do przedziału :
(10
29,10
30).
16 mar 22:21
Benny: Masz rację będzie 1031, nie pomnożyłem w sumie przez a1
16 mar 22:28
Benny:
Co do tego zadanka z sześcianem: korzystamy z trójkątów podobnych i wszystko ładnie wychodzi

Zadanko 3, nie ogarniam tego wierzchołka
Przecież może to wyglądać tak i f(0) będzie <0
16 mar 22:35
Mila:
dla
p=1 mamy :
−4*2
x+3=0
4*2
x=3
| | 3 | |
2x= |
| to równanie ma rozwiązanie. |
| | 4 | |
16 mar 22:36
Benny: Ups, ja nie wiem co ja modziłem w tym zeszycie, ale gdy liczyłem dla p=1 pominąłem drugi wyraz
i napisałem, że sprzeczność

Tak poza tym reszta ok?
16 mar 22:40
Mila:
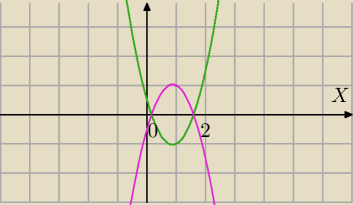
Takie sytuacje nam odpowiadają w zadaniu 3.
Δ>0 i x
w∊(0,2) i podane warunki wcześniej.
16 mar 22:49
Benny: a w tym drugim p∊(−2;2>?
16 mar 22:57
Mila:
Tak.
16 mar 23:02
Benny: Coś nowego do roboty się jeszcze znajdzie?

16 mar 23:05
Mila:
5)
W ostrosłupie SABC wszystkie kąty płaskie przy wierzchołku S sa proste.
Pola ścian bocznych SAB,SAC i SBC są odpowiednio równe: 3,4,6.
Oblicz objętość ostrosłupa.
16 mar 23:23
5-latek: Uwaga : Gdy patrzymy w dol to prosta wzdluz ktrorej patrzymy tworzy pewoen kat z plaszcyzna
pozioma przechodzaca przez oko. Kąt ten nazywamy depresją .
Podobnie gdy patrzymy w gore to kierunek w ktorym patrzymy tworzy z ewspominiana plaszczyzna
poziona kat zwany elewacją , czyli wzniesieniem
Zadanie nr 1 .
Elewacje drzewa rosnacego po drugiej stronie rzeki mierzymy dwukrotnie; raz w punkcie A nad
brzegiem rzeki drugi raz w punkcie B odleglym od A o 25m . Drzewo znajduje sie na prostej AB
. Obliczyc wysokosc drzewa i i odleglosc od a do drzwewa gdy zanlezione elewacje rownaja
sie odpowiednio 62o i 48o.
Zadanie nr 2.
Balon wznosi sie pionowo . W chwili gdy znajduje sie on na wysokosci h metrow nad ziemia
lotnik mierzy kąt depresji x pewnego przedmiotu na ziemi . Po uplywie t sekund powtarza ten
pomiar i otrzymuje kąt x' . Z jaka predkoscia srednia wznosi sie balon.
Zadanie nr 3.
Na plaszzcyznie poziomej lezy otworem do gory polkula zelazna wewnatrz prozna ,promien polkuki
r=6cma scianki maja 0,5cm grubosci . W polkuli tej lezy cienki prosty drucik dlugosci
13cm,tak ze czesc drucika wystaje na zewnatrz . Natoniast czesc znajdujaca sie wewnatz polkuli
widziana jest z jej srodka pod kątem 100o .
Na jakiej wysokosci nad stolem znajduja sie gorny i dolny koniec drucika .
17 mar 17:04
Benny: Masakra z tym zadaniem co w szkole modziłem. Za pierwszym razem źle przeczytałem treść, bo
wyszło mi, że one są do siebie w stosunku 3,4,6 i tak liczę liczę i coś mi nie wychodzi no i
skąd ta niewiadoma cały czas w bokach. Później zauważyłem, że to jednak są pola, więc liczę,
liczę znowu coś nie pasuje jakieś pierwiastki mi powychodziły. Co było błędem? Pole trójkąta
nie podzieliłem przez 2. Dopiero teraz jak usiadłem w spokoju, narysowałem sobie jeszcze raz.
Boki ładnie powychodziły, pozaznaczałem kąty proste i ładnie wyszło 4j
3. W ogóle to miałem
już tu coś kombinować z jakimiś sinusami i cosinusami, bo nie mogłem ogarnąć jak tu będzie z
tym spodkiem wysokości.

17 mar 17:20
Mila:
odp. dobra.

17 mar 17:26
Benny: Te najłatwiejsze zadania często są dla mnie trudne, ponieważ zawsze kombinuje a w takich
zadaniach aż za bardzo. Przykładem jest ostatnia próbna matura PODSTAWOWA Lubelska bodajże.
Było tam zadanie z dowodem geometrycznym, trzeba było wykazać, że dwa trójkąty mają równe
pola. Narysowałem sobie wszytko ładnie, ale tego nie widziałem a wszystko na rysunku już było.
17 mar 17:44
Benny: 5−latek,
zadanko nr 1
h=17,5m
odległość A do drzewa x=9,25m
Zadanko nr 2
17 mar 17:56
Benny: Milu, a co myślisz o jakimś prawdopodobieństwie? Bo zazwyczaj dają jedno zadanko z
prawdopodobieństwa na indeksie, a chyba z tego trochę leżę(nie lubię)

17 mar 17:58
5-latek: Oba zle masz .
Zadanie nr 1 h=67,8 odleglosc 36,05m
Zadanie nr 2
17 mar 18:20
Benny: Pokaż mi to na rysunku pierwsze, a to drugie to czemu tak?
17 mar 18:26
Benny: To drugie na bank jest dobrze

17 mar 18:28
5-latek: To sa stare zadania nie ma rysunkow (musisz zrobic sam
| | 25 | |
h= |
| = ctg jest funkcja malejaca wiec ctg48 jest wiekszy od ctg 62 |
| | ctg48−ctg62 | |
Zadanie 1 i 3 oznaczone sa jako trudne
17 mar 18:32
5-latek: Nr 2
s − droga przebyta przez balon pomiedzy pomiarami
u− odleglosc miejsca startu balonu od przedmiotu na ziemi
Rozwiaz ten uklad ze wzgledu na s (droge
17 mar 18:38
5-latek: Podam CI odpowiedz do nr 3
Dolny koniec x=6,5−6*sin80= 0,59cm
gorny y= x+13*sin40=8,59cm
17 mar 18:47
Benny:
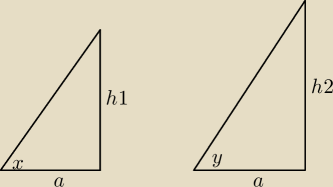
Ja to zrobiłem tak:
h
2−h
1=s
h
1*ctgx=h
2*ctgy
17 mar 18:53
5-latek: | | ctgx | |
To pewnie bedzie to samo bo jak sprowadzidz |
| −1 do wspolnego mianownika to wyjdzie |
| | ctgy | |
tak samo
17 mar 18:57
Benny: Milu, jestem głodny zadanek, jutro w szkole będę miał dużo czasu, którego nie można
marnować

17 mar 21:55
Mila:
Jakiego typu tam były na indeksie z prawdopodobieństwa, to coś znajdę.
17 mar 21:56
17 mar 22:01
Mila:
1) W trzynastu rzutach symetryczna kostką do gry otrzymano 3 razy szóstkę.
| | 3 | |
Oblicz prawdopodobieństwo, że otrzymano szóstkę w siódmym rzucie. ( |
| |
| | 13 | |
17 mar 22:32
Benny: Dziękuje, a teraz uciekam spać.
Dobranoc

17 mar 22:40
Mila:
2)
Ze zbioru liczb {1,2,3,4,5,6,7,8,9,10} wybieramy w sposób losowy kolejno dwie liczby i od
pierwszej odejmujemy drugą . Jakie jest prawdopodobieństwo,ze różnica jest większa od 2?
17 mar 22:44
Mila:
Dobranoc

17 mar 22:45
5-latek: Zadanie nr1.
Wykaz ze jezeli zdarzenia A i B sa niezalezne to zdarzenia A'i B' sa takze niezalezne
Zadanie nr 2.
Jest 50 pytan egzaminacyjnych. Kazdy zdajacy losuje kartke z 3 pytaniami . Ile moze byc
zestawow pytan?.
Niech A
k(k=0,1,2,3) oznacza zdarzenie : zdajacy umie odpowiedz na k pytan z kartki .
Obliczyc P(A
k) przy zalozeniu ze zdajacy zna odpowiedz na 25 pytan .
Obliczyc prawdopodobienstowo p ze zdajacy odpowie conajmniej na jedno pytanie .
Na dzisiaj starczy . Potem odpocznij

18 mar 14:33
Benny: Zadanka od [F[Mili],
nr 1
|Ω|=13*12*11*10
5
|A|=3*12*11*10
5
nr 2
|Ω|=100
A'−różnica liczb jest równa 0,1,2
|A'|=10+9+8=27
Tego zadania nie jestem pewny. Moje rozumowanie jest takie:
jeśli różnica liczb jest równa 0 to liczba pierwsza ma być taka sama jak druga więc jest takich
możliwości 10, różnica jest równa 1− tutaj już będzie 9 możliwości, ponieważ pierwsza liczba
nie może być 1, różnica jest równa 2− 8 możliwości, ponieważ pierwsza liczba nie może być 2.
Dobrze myślę?

18 mar 16:48
Mila:
1) z błędem.
Na każde z 10 pozostałych miejsc wybierane są wyniki na 5 sposobów ze zbioru {1,2,3,4,5}
2)Źle.
Zrób tabelke dla zbioru {1,2,3,4,5} potem uogólnij.
18 mar 17:00
Benny: 5
10 zamiast 10
5?

18 mar 17:02
18 mar 17:08
Benny: To za pomocą tabelki wychodzi |A|=28
inny sposób niż tabelka?
18 mar 17:11
Mila:
2) Popraw rozumowanie, zauważ, że losowanie jest bez zwracania.
Różnica większa od 2, czyli 3,4,5,6,7,8,9,
Wyników 28.
1+2+3+4+5+6+7=28
(4,1)
(5,1),(5,2)
(6,1), (6,2),(6,3)
.
.
(10,1),(10,2),(10,3),(10,4),10,5),10,6),(10,7)
18 mar 17:26
18 mar 17:36
Mila:
Zgadza się.
Kiedy pisesz ten indeks?
18 mar 17:38
Benny: W niedziele godzina 13
18 mar 17:47
Benny: Nie leżą mi te zadanka z prawdopodobieństwa, za krótko się tego uczyłem.
18 mar 18:33
Mila:
Masz dużo jeszcze czasu, nadrobisz .
18 mar 18:37
Mila:
3) Oblicz prawdopodobieństwo, że przy czterokrotnym rzucie kostka sześcienną trzy kolejne
wyniki utworzą ciąg geometryczny.
18 mar 18:46
Mila:
Załóż nowy wątek.
18 mar 18:58
Agnieszka : 5m − 2n + 12 dla m = 3,n = 4
3 cze 13:58








 Ostatnio coś pisałeś, że dołożysz jakieś zadanka z ciągów, pochodnych i
planimetrii. Dawno nie rozwiązywałem zadanek od Mili
Ostatnio coś pisałeś, że dołożysz jakieś zadanka z ciągów, pochodnych i
planimetrii. Dawno nie rozwiązywałem zadanek od Mili 

 Dawaj sprobuje . najwyzej pojade do dr. Gewerta albo Skolczylasa . Niech rozwiazuja . A co mi
to
Dawaj sprobuje . najwyzej pojade do dr. Gewerta albo Skolczylasa . Niech rozwiazuja . A co mi
to  Tak powaznie to jeszce nie teraz
Tak powaznie to jeszce nie teraz

 Juz sobie go zapisuje
Juz sobie go zapisuje


 Nr1 .
W zwiazku z tym ze a,b,c, i h tworza ciag geometryczny to a:b=c:h
wiec a*h= b*c
Ale wiemy ze a*h to podwojona wartosc pola trojkata ABC (tak ?
Wiemy tez ze 2P= b*c*sin CAB(tez wiadomo
wiec wobec rownosci a*h=b*c mozemy zapisac ze b*c*sinCAB=b*c to sin CAB=1 to
CAB=90o (czyli trojką prostokątny
Nr1 .
W zwiazku z tym ze a,b,c, i h tworza ciag geometryczny to a:b=c:h
wiec a*h= b*c
Ale wiemy ze a*h to podwojona wartosc pola trojkata ABC (tak ?
Wiemy tez ze 2P= b*c*sin CAB(tez wiadomo
wiec wobec rownosci a*h=b*c mozemy zapisac ze b*c*sinCAB=b*c to sin CAB=1 to
CAB=90o (czyli trojką prostokątny



 Pozdrawiam .
Potem jesli bedziesz chcial to wrocisz do moich OK?
Pozdrawiam .
Potem jesli bedziesz chcial to wrocisz do moich OK?

 |AB|2=|BC|2 + |CA|2
|AB|=r1+r2
|BC|=3−y
|CA|=x
|AB|=4−y+1−5=5−y
(5−y)2=x2+(3−y)2
|AB|2=|BC|2 + |CA|2
|AB|=r1+r2
|BC|=3−y
|CA|=x
|AB|=4−y+1−5=5−y
(5−y)2=x2+(3−y)2

 no a co z tym przedziałem (0;2)?
no a co z tym przedziałem (0;2)?


 Co do tego zadanka z sześcianem: korzystamy z trójkątów podobnych i wszystko ładnie wychodzi
Co do tego zadanka z sześcianem: korzystamy z trójkątów podobnych i wszystko ładnie wychodzi  Zadanko 3, nie ogarniam tego wierzchołka
Przecież może to wyglądać tak i f(0) będzie <0
Zadanko 3, nie ogarniam tego wierzchołka
Przecież może to wyglądać tak i f(0) będzie <0
 Tak poza tym reszta ok?
Tak poza tym reszta ok?
 Takie sytuacje nam odpowiadają w zadaniu 3.
Δ>0 i xw∊(0,2) i podane warunki wcześniej.
Takie sytuacje nam odpowiadają w zadaniu 3.
Δ>0 i xw∊(0,2) i podane warunki wcześniej.





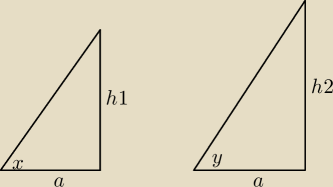 Ja to zrobiłem tak:
h2−h1=s
Ja to zrobiłem tak:
h2−h1=s





