proszę o rozwiązanie
Michał: Punkt P jest środkiem krawędzi AB , punkt Q − środkiem krawędzi CC
,
a punkt R − środkiem krawędzi AD sześcianu ABCDA
, B
,C
,D
, o boku długości a
Oblicz pole przekroju sześcianu płaszczyzną wyznaczoną przez te punkty.
przekrojem jest pięciokąt foremny
| | √2 | |
obliczyłem IPRI = |
| *a który jest również bokiem pięciokąta foremnego
|
| | 2 | |
nie wiem czy dobrze zacząłem
15 mar 18:27
Michał: jest wzór na obliczenie pola pięciokąta foremnego
ale mam problemy z obliczeniem tego pola może ktoś ma jakiś pomysł
15 mar 20:43
Mila:
Przekrój nie jest pięciokątem foremnym.
16 mar 16:14
Benny: Mi tu wychodzi trójkąt co najlepsze równoramienny?
16 mar 17:06
Mila:
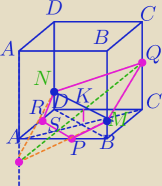
16 mar 21:10
Benny: Ok już widzę mój błąd w rozumowaniu. Ja po prostu zaznaczyłem figurę RPQ, a nie przekrój całego
sześcianu
16 mar 21:20
Michał: rzeczywiście będzie to pięciokąt który jest podzielony na trapez i trójkąt równoramienny
| | a*√2 | |
czyli PR= |
| MN = a√2
|
| | 2 | |
jeżeli to dobrze obliczyłem to QK będzie wysokością trójkąta NMQ a KS wysokością trapezu
które na razie nie wiem jak obliczyć
16 mar 22:13
Michał: rzeczywiście będzie to pięciokąt który jest podzielony na trapez i trójkąt równoramienny
| | a*√2 | |
czyli PR= |
| MN = a√2
|
| | 2 | |
jeżeli to dobrze obliczyłem to QK będzie wysokością trójkąta NMQ a KS wysokością trapezu
które na razie nie wiem jak obliczyć
16 mar 22:18
Benny: Dobrze myślisz. Poszukaj trójkątów podobnych

16 mar 22:37
Michał: prawdę mówiąc nie widzę trójkątów podobnych
16 mar 23:38
Michał: prawdę mówiąc nie widzę trójkątów podobnych
16 mar 23:41
Mila:
Z punktu K masz poprowadzoną różową prostopadłą, ten ma trójkącik jest podobny do ΔSCQ.
16 mar 23:42
Michał: KO ⊥ SC ΔSOK podobny do ΔSCQ to
| KO | | SK | | 1 | |
| = |
| KO = |
| CC,
|
| QC | | SQ | | 2 | |
nie wiem czy dobrze
17 mar 20:34
Michał: nie wiem czy dobrze określiłem podobieństwo trójkątów
18 mar 19:09
18 mar 19:17
Michał: muszę coś obliczać żle bo nie mam takiego wyniku
18 mar 22:56
18 mar 23:22
Michał: | | 1 | | 3√2a | | 1 | |
ISOI = |
| √2a ISCI= |
| IQCI = |
| a
|
| | 4 | | 4 | | 2 | |
| | a√5 | |
z Δ SOK IKOI2 + ISOI2 = ISKI2 ⇒ ISKI = |
|
|
| | 6 | |
| | a√2 + 0,5a√2 | | a√5 | | a2√10 | |
PPRNM= ( |
| )* |
| = |
|
|
| | 2 | | 6 | | 4 | |
| | 11a2 | | √11a | |
ISQI2 = ISCI2 + ICQI2 ⇒ ISQI2 = |
| ⇒ ISQI = |
|
|
| | 8 | | 2√2 | |
| | 3√22a − 2√10 | |
IKQI = ISQI − I SK I ⇒ IKQI = |
|
|
| | 12 | |
P
RPMQN = P
PRNM + P
NMQ
| | 7a2√11 | |
a z ostatniego działania nie będzie wyniku P = |
|
|
| | 24 | |
20 mar 21:22
Mila:
| | a | | 1 | |
|SK|2=( |
| )2+( |
| a√2)2⇔ |
| | 6 | | 4 | |
Teraz licz.
20 mar 21:38
Michał: | | a2√11 | | √11a | |
PRPMN = |
| ISQI2 =ISCI2 + IQCI2 ⇒ISQI = |
|
|
| | 8 | | 2√2 | |
| | a√11 | |
IKQI = ISQI − ISKI ⇒ IKQI = |
|
|
| | 3√2 | |
| | a2√11 | | a2√11 | | 7a2√11 | |
PPMQNR = |
| + |
| = |
|
|
| | 6 | | 8 | | 24 | |
dziękuję bardzo i przepraszam za pomyłki przy obliczeniach
21 mar 12:07

