Maturalne zadanka :) Benny: W(x)=64x³ + 48x² + px + q jeśli wielomian jest stopnia trzeciego i ma mieć pierwiastek trzykrotny to istnieje tylko jeden taki (4x−a)³=64x³ − 48x²a + 12xa² − a³ −48x²a=48x² −a=1 a=1 12xa²=px 12a²=p q=−1 p=12 inny pomysł na chwilę obecną mi nie przychodzi

Benny: Co do Twojego zadania 5−latek mianownik sprowadza się do 2/cosx w liczniku mamy takie coś : √cos²x − |cos2x| dla x∊(−π/4 +kπ/2 ; π/4 + kπ/4) jest √cos²x − cos2x=√cos^x − 2cos^x +1= =√1−cos^x=√sin²x=|sinx| no i dla sinx>0 będzie sinx/4 a dla sinx<0 −sinx/4 tylko nie wiem jak ten przedział zapisać w tej wcześniejszej wartości bezwzględnej |cos2x| dla cos2x<0 wychodzi bezsens

Mila: a=−1 −a³=q q=1 p=12 Inne sposoby. 1)Wzory Viete'a 2) Wykorzystanie pochodnej.

Benny: ach widzę ten błąd przy a wzory Viete'a? chodzi Ci o ten na wielomian 3 stopnia? sprawdzę jak to będzie z pochodną

Mila: http://pl.wikipedia.org/wiki/Wzory_Vi%C3%A8te%E2%80%99a

Mila:

Mila: 2) Jednym z pierwiastków wielomianu W(x) stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu wielomianu należy punkt P(3,1). Wiedząc, że reszta z dzielenia W(x) przez dwumian (x−2) jest równa (−2) wyznacz wzór tego wielomianu i uporządkuj go malejąco.

Benny: no kiedyś obiło mi się o tych wzorach o uszy co do pochodnej f'(x)=192x² +96x +p Δ=0, p=12 f'(x)=16(x+1/4)² miejsce zerowe pochodnej x=−1/4 no i tutaj nie jestem pewien, ponieważ miejsce zerowe pochodnej wstawiłem do funkcji podstawowej i o dziwo mi wyszło q=1 ale nie wiem czy taki myk można zrobić?

Mila: http://encyklopedia.pwn.pl/haslo/pierwiastek-wielokrotny;3956914.html

Mila: Dobrze.

Benny: W(x)=(x−1)(ax² +bx +c) W(3)=1 W(2)=−2 −b/a=0 b=0 W(x)=(x−1)(ax² + c) W(3)=18a +2c W(2)=4a+c

⎧	18a+2c=1
⎩	4a+c=−2

⎧	18a+2c=1
⎩	−8a−2c=4

10a=5 a=1/2 c=−4 W(x)=x³/2 − x²/2 −4x −4

Mila: Mam c=4

Benny: no tak patrze i nie widzę błędu u siebie

Benny: W(x)=x³/2 − x²/2 − 4x+4

Mila: 3) Rozwiąż równanie: (x²−x+1)³−6*(x²−x)²−2*(x²−x+2)=0

Mila: 4) Rozwiąż równanie.

	9
[x]=		x+1
	10

PW: 5) Porównaj liczby x₁ = √378 − √377 x₂ = √375 − √374. Oczywiście nie można korzystać z kalkulatora. Wskazówka (nawiązanie do dzisiejszych zmagań z funkcją malejącą): Pomyśl o rozwiązaniu wykorzystującym monotoniczność pewnej funkcji − wymyśl ją i wykaż monotoniczność za pomocą pochodnej. Bardzo jestem ciekawy, czy nauka nie poszła w las.

Benny: Jakaś mała podpowiedź do tego 3, bo raczej nie chodzi o wymnożenie wszystkiego. Próbuje coś wyłączyć zobaczymy czy będą efekty

Mila: Do (3) Podstawienie:

Mila: Do (3) x²−x=t

Mila: Dobranoc

Benny: t=x²−x+1 t³ −6(t−1)² −2(t+1)=0 t³ −6t² +10t−8=0 (t²−2t+2)(t−4)=0 t>0 więc t²−2t+2 >0 t=4 x²−x+1=4 x²−x−3=0 x₁=(1−√13)/2 x₂=(1+√13)/2

Benny: zrobiłem inne podstawienie, bo nie widziałem Twojego posta co do 4 nie rozumiem zapisu dobranoc

5-latek: Co do zadania nr 4 to dostalem je tak samo od Mili do rozwiazania Na razie nie potrafie go rozwiazac . Sprobuje pozniej (wieczorem a [x] −oznacza czesc calkowita liczby nie wieksza od tej liczby −raczej zadania olimpijsie

[Z[prosta]]: ad.4 (wydawało mi się, że zadania z [x] mnie przerastają, a jednak...)

	9
gdy narysujemy wykresy funkcji y=[x]−1 oraz y=		x widać, że przetną się w jednym
	10

punkcie ...lewe końce "odcinków" budujących wykres funkcji y=[x]−1 leżą na prostej: y=x−1

	9
rozwiązując układ: y=x−1 i y=		x otrzymuję : x=10, y=9
	10

Stąd równanie ma jedno rozwiązanie: x=10

5-latek: Natomiast co do mojego zadania z trygonometrii to lewa strona rownania ma sens jesli :1^o cos2x ≥0 co zachodzi gdy −0,25pi+kpi≤x≤0,25pi+kpi (k=0 +/−1,+/−2 ...) 2^o cos^x−cos2x≥0 co

	3
zachodzi zawsze bo cos2x−cos2x=sin2x≥0 3o 1+sinx≠0 co zachodzi gdy x ≠2kpi+		pi
	2

	1
(k=0 k=+/−1. k=+/−2 .....) 4o cosx≠0 wtedy gdy x≠kpi+		pi (k=0 , k= +/− 1,
	2

	3
k=+/−2........) 5o cosx+1+2sinx+sin2x=2(1+sinx)≠0 co zachodzi gdy x≠2kpi+		pi (k=0
	2

k=+/−1 k=+/−2 ........) Teraz zauwaz ze liczby z warunkow 3^o 4^o 5^o leza poza przedzialami okreslonymi warunkiem 1^o , wiec warunek 1^o jest wystaerczajacym warunkiem aby lewa strona nierownosci miala sens . Przeksztalcenia po lewej stronie beda wygladac tak ;

	√cos2x−cos2x
L=		=
	cos2x+1+2sinx+sin2x   (1+sinx)cosx

	√sin2x cosx(1+sinx)
=		=
	2+2sinx

	|sinx|cosx(1+sinx)
=		=
	2(1+sinx)

1		1
	|sinx|cosx=		*2|sinx|cosx
2		4

Z tych przeksztalcen widac ze ze lewa strona L na znak cosinusa a prawa strona P na znak funkcji sin2x wiec mozemy to zestwic w postaci nierownosci

	1		1
6o. znak cosinusa cosx>0 gdy −		pi+2kpi< x <		pi+2kpi
	2		2

	1
7o znak funkcji y=sin2x: sin2x>0 gdy kpi<x<		pi+kpi
	2

teraz gdy uwzglednimy warunek nr 1⁰ przy ktorym lewa strona rownosci ma sens to z tych trzech warunkow a mianowicie z warunkow 1^o 6^o i 7^o wynika ze :

	1
Po prewej stronie stawiamy znak (−) gdy −		pi+kpi< x < kpi
	4

	1
Natomiast stawiamy znak (+) gdy kpi<		pi+kpi (k=0,k=+/−1, k=+/−2 k=+/−3,.....)
	4

5-latek: Dziekuje Ci Eve za post 9:02 Ja poczytam sobie jeszce na ten temat bo musi tez byc sposob na rozwiazanie algebraivzne

5-latek: W warunku 2^o ma byc cos²x−..... itd

Benny: No zapomniałem o dziedzinie z mianownika ale chyba szedłem dobrą drogą

5-latek: No chyba na złą nie zejdziesz ?

Benny: Nie wiadomo co życie przyniesie

Benny: co do 4) to szukałem podobnych zadań ale nie mogę znaleźć jak rozwiązywać takie równania co do 5) próbowałem pod pierwiastek wstawić zmienną ale chyba nic mi nie wychodzi

5-latek: Co do zadan podobnych do nr 4 to chyba zostalo Kolko dla olimpijczykow Pawlowski

Mila: Benny Zadanie 3 dobrze. Ładnie to rozwiązałeś. 4) Podpowiedź : [x]=m, m∊C m≤x<m+1

5-latek: Mozesz Milu to pokazac jak rozwiazac ? Wiem ze taka jest wlasnosc czesci calkowitej

5-latek: nawet doczytalem sie ze [x+k]= [x]+k gdzie x∊r i k∊C

5-latek: Probowalen to robic ze 10[x]= 9x+10 ale to mi nie da

Mila: Poczekaj, zobaczymy jak rozwiąże Benny, później napiszę.

5-latek: Dobrze .Poczekam

Benny: Skąd w ogóle takie zadanie?

5-latek: Przeciez CI napisalem albo Stefan Straszsewicz Zadania olimpijkie albo Jerzy Browkin Zadania z olimpiad matematycznych

5-latek: Milu bardzo CIe proszse o pokaznie rozwiazania gdyz kolega chyba tez nie bedzie wstanie rozwiazac tego rownania

Benny: Z tego równania co podałaś wychodzi że m<10;20) ale tylko dla m=10 wyrażenie jest całkowite nie mam chyba pojęcia co dalej

Mila: Przeczytałeś wskazówkę. Wierzę w Ciebie. Rozwiązuj.

Mila: Przedział podałeś dobry. Jesteś blisko.

Benny: Przynajmniej jutro w szkole się nie będę nudził

Mila: Masz rozwiązać teraz. Czekam.

Benny: Głowa mnie trochę boli i miałem kłaść się już spać bo trzeba rano wstać

Benny: Dziś już nic nie wymyślę. Dobranoc

Mila: Do jutra. DOBRANOC.

5-latek: https://matematykaszkolna.pl/forum/283512.html Zobacz moje rozwazania Milu Ja pewnie juz bede w pracy jak spojrzysz

Benny: PW, coś tam się pobawiłem i sam już nie wiem co zrobiłem. za 378 podstawiłem x itd. więc miałem pierwszą liczbę: √x−√x−1, drugą liczbę:√x−3 − √x−4 funkcja wygląda tak: f(x)=√x−√x−1−√x−3+√x−4 wyznaczyłem pochodną i policzyłem dwie wartości oczywiście z przybliżeniem i wyszło mi że funkcja jest malejąca więc jeśli zwiększamy x wartość maleje co za tym idzie x₂>x₁ O to chodziło?

PW: Prościej, f(x) = √x − √x−1 jest malejąca; nierówność f'(x) < 0 jest oczywista. Wobec tego x₁ = f(378) < f(375) = x₂. Zauważ, że zadanie jest dobrze skonstruowane, bo różnicę widać dopiero na 4. miejscu po przecinku, kalkulatorem nastawionym np. na dokładność do 3 miejsc nie da się rozstrzygnąć, która liczba jest większa.

Mila:

	378−377		1
√378−√377=		=
	√378+√377		√378+√377

Benny: Jeszcze parę takich zadań i powinienem to ogarnąć

PW: Mila ma rację, że dużo łatwiej jest odpowiedzieć która liczba jest większa przekształcając x₁ i x₂ w sposób pokazany o 19:25 − tak mógłby rozwiązać nawet gimnazjalista. Chciałem pokazać tę różnorodność podejścia − czasem w sposób niespodziewany daje się zastosować własności funkcji (pochodne). Dobrze jest widzieć i takie możliwości. Benny, łapiesz − i to jest ważne.

Benny: Dziś coś porozwiązujemy?

Pati: Mila możesz pomóc z jednym prawdopodobieństwem ?

Benny: Milu, rozwiązujemy coś?

Mila: Możemy, myślałam, że to było pytanie do PW. Zaraz coś znajdę.

Mila: 1) Narysuj wykres funkcji : y=[sinx]

Mila: 2) O wielomianie W(x)=2x³+ax²+bx+c wiadomo, że liczba 1 jest jego pierwiastkiem dwukrotnym oraz , że W(x) jest podzielny przez dwumian (x+2). Oblicz wsp. a,b,c . Rozwiąż nierówność: W(x+1)<0.

Benny: [sinx]=m, m∊C więc będzie przyjmowała wartości albo 0 albo 1 albo −1 tak?

Mila: Tak, ale rozpisz to w przedziale <0,2π>. [sinx]=0 dla sinx∊... itd

Benny: kurde tak się zastanawiałem nad tym wielomianem i czy nie może być tak: W(x)=a*(x−1)²(x+2) W(x)=a*(x³−3x+2) W(x)=ax³ −3ax +2a przy x³ stoi 2 więc to a jest równe 2 więc wielomian jest taki W(x)=2x³ −6x+4 więc a=0, b=−4 c=4?

Benny: a W(x+1)<0 x∊(−∞;−3)

Mila: Masz kolizję oznaczeń. W(x)=2*(x−1)²*(x+2) a=0, b=−6,c=4 Dalej, dokończ.

Benny: no błąd źle zapisałem, b=−6 a [−1/2]=0?

Mila: [−¹₂]=−1

Benny: a np [−1,6]=−2?

Mila: Tak. Tu popatrz. https://matematykaszkolna.pl/strona/979.html

Benny: [sinx]=0 dla x={0,π,2π} [sinx]=1 dla x∊(0;π) [sinx]=−1 dla x∊(π,2π) tak?

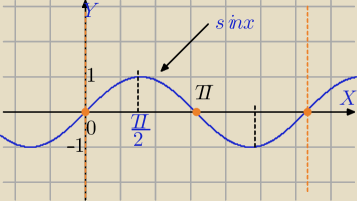
Mila: Dla przedziału <0,2π> y=[sinx] [sinx]=0 dla sinx∊<0,1) [sinx]=1 dla sinx=1 [sinx]=−1 dla sinx∊<−1,0) ⇔

	π		π
[sinx]=0 dla x∊<0,		)∪(		,π)∪{2π}
	2		2

	π
[sinx]=1 dla x=
	2

[sinx]=−1 dla x∊(π,2π) Czy narysować, czy sam to zrobisz?

Benny: Aj pomyliło mi się z tą jedynką przecież [0,7]=0

Benny: A wykres wiem jak ma wyglądać tylko nie wiem czy dam rade tutaj rysunek zrobić

Benny: Milu jak będziesz możesz jakieś zadanka podrzucić?

Benny: Może ktoś inny coś wrzuci? Porobiłbym sobie coś w szkole

5-latek: Zadanie nr 1 : Dla jakich wartosci parametru a dwa z podanych nizej zdan sa prawdziwe a jedno falszywe

	1
a) rownanie x+		=a nie ma rozwiazan
	x

b) √a³−4a+4=2−a c) Uklad rownan x+y²=a i x−sin²y=−3 ma dokladnie jedno rozwiazanie Zadanie nr 2 : Wyznaczyc zbior wszystkick par (x,y) liczb rzeczywistych dla ktorych wyrazenie ⁴√4−x²−y²−U{1}{√y−logx ma wartosc rzeczywista . Zbior ten przedstawic graficznie na plaszczyznie 0XY Zadanie nr 3 na plaszczyznie 0XY zaznaczyc zbior punktow ktorych wspolrzedne x,y spelniaja warunki 1. x²+y²>=2 2. Najwieksza wartosc sumy |x|+|y| nie przekracza 2 . Zadanie nr 3 . Sprowadzic do mozliwie prostej postaci wyrazenie

	a3/2−b3/2		a−2/3 3√a−b
W=		:
	(a2−ab)2/3		a√a−b√b

Zadanie nr 4. Zbadac jaka wartosc powinien miec parametr m aby pierwiastki rownania 3x²+mx+1=0 mogly byc sinusem i cosinusem tego samego kąta . Znalezc ten kąt i oba pierwiastki . Zadanie nr 5 : Rozwiazac uklad rownan a) √x²+y²+√2xy=8√2 i √x+√y=4

	1		1
b) √x+y−		=2 i x+y−		=8
	√x−y		√x−y

Zadanie nr 5 Jaki zwiazek musi zachodzic pomiedzy aib(a>b,b>0) aby

	1		1
log		(a+b)=		(loga+logb)
	3		2

Zadanie nr 6 Wyznacz najwieksza liczbe x dla ktorej spelnione jest zarowno rownanie

	3		3		7
(		)x−y−(		)y−x=		jak i nierownosc xY+y<=9
	4		4		12

Zadanie nr 7

	5
Rozwiaz nierownosc log2(x+1)+logx+12>=
	2

Zadanie nr 8 Wyznacz okres funkcji y=|4sin³x−3sinx| Mysle ze na razie CI starczy . Potem CI napiszse innne

bezendu: ok

5-latek: jak wroce z pracy po 23 napiszse jeszcze z ciagow , pochodnych i z planimetrii po zadanku

5-latek: Nie odswiezylem strony Czesc bezendu

bezendu: Witam

Benny:

	a3+b3−2√(ab)3
w zadaniu 3 ma wyjść W=		?
	a−b

Benny: w 1 a) a∊(−2;2) b)a<2 c)a>−3? tego nie ogarniam bo mam tak −3 + sin²y+y²=a sin²y+y²>0 no i tak myślę, że z tego wynika a>−3

5-latek: zadanie nr 3 dla a>0,b≥0 a≠b

	(a√a−b√b)2
W=
	a−b

5-latek: Czyli wyjdzie to co Tobie

5-latek: Zadanie nr 1 Zdanie a) jest prwadziwe gdy a∊A=(−2,2). Zdanie b) jest prawdziwe gdy 2−a≥0 to a≤2 oraz gdy a³−4a+4=(2−a)² a to jest spelnione dla a=0 lub a=1 . czyli zdanie b jest prawdziwe gdy a∊B={0,1}. Zdanie c) jest prawdziwe gdy po odjeciu stronami otrzymany rownanie y²+sin²y=a+3 i to rownanie ma dokladnie jesden pierwiastek . Bowiem x wyraza sie przez y jednoznacznie z kazdego danych rownan. Lewa strona rownania jest funkcja parzysta ze wzglewdu na y a prawa jest stala . Aby wiec to rownanie mialo dokladnie jeden pierwiastek musi byc nia liczba y=0 . Gdy podsatwimy y=0 do tego rownania to dostaniemy 0=a+3 to a=−3 . A wiec rownanie bedzie mialo postac y²+sin²y=0 . Teraz widzimy ze y=0 jest jedynym pierwiaskiem rownania y²+sin²y=0 Wiec zdanie c) jest prawdziwe dla a=−3 tj . dla a ∊C={−3} . Wiec mamy ze zdania a),b) c) sa prawdziwe dla a ∊A , a∊B i a∊C. Wiec warunki naszsego zadania sa spelnione gdy a nalezy do dwoch sposrod tych zbiorow a nie nalezy do trzeciego a wiec gdy : a∊(A∩B−C)U(A∩C−B)U(B∩C−A)= [(−2,2)∩{0,1}−{−3}U[(−2,2)∩{−3}−{0,1}]U[{0,1}∩{−3}−(−2,2)]={0,1} warunki zadania sa spelnione gdy a=0 lub a=1

5-latek: No to dawaj zadanie nr 2

Benny: Kurcze nie wiem jak to tutaj narysować. Ogólnie to będzie układ równań

⎧	y>logx
⎩	y≤√4−x2	dla x∊(0;2>

Benny: W tym zadaniu 3 to jest układ równań czy podpunkty? Bo w 1. będzie wszystko oprócz koła o środku w punkcie O(0;0) i r=√2 a w 2. będzie kwadrat o środku S(0;0) i boku równym 2√2 (osie współrzędnych są przekątnymi) W zadaniu 4 m=√15 lub m=−√15 pierwiastki równania x₁=−0,93 x₂=−0,36 lub x₁=0,36 x₂=0,93 kąt wynosi 21 stopni lub −21 stopni Zadanie 5 a) x=4, y=4 b) x=5, y=4

5-latek: zadanie nr 3 sa to podpunkty (ja tak przynajmniej to odczytuje (mozesz tu narysowac i opisac Zadanie nr4 parametr m dobrze

	1		1
Potem mam takie odpowiedzi dla m=−√15 x1=		(√15−√3), x2=		(√15+√3)
	6		6

Natomiast jesli kat oznqaczymy przez (t) to

	1		1
sin(t)=		(√15−√3) cos(t)=		(√15+√3)
	6		6

	1		1
lub sin(t)=		(√15+√3) cos(t)=		(√15−√3)
	6		6

Podobnie postepujemy gdy m=−√15 Zadanie nr 5 (gdzie uklady mam takie same odpowiedzi

Benny: No w tym 4 wszystko mi tak samo wyszło tylko zaokrąglałem liczby, żeby obliczyć kąt Teraz się zastanawiam nad tym zadankiem z logarytmami.

5-latek: Odpowiedz do zadania z logarytmem a+b=3√a*b

Benny: a no jak tak to banalne, zrobiłem tak na początku myślałem, że coś tu jeszcze trzeba kombinować

5-latek: To sa zadania z egzaminow wstepnych na wyzszse uczelnie

Benny: Na jaki kierunek?

5-latek: A jaki Cie interesuje to napiszse CI kilka zadan ze starych zbiorkow

Benny: Właśnie nie mam żadnego pomysłu, gdzie się wybrać na studia

5-latek: Ale teraz nie ma egzaminow wstepnych ? Rozwiaz tamte do konca zadania potem wstawie CI nowe

Metis: 5−latku , nie ma

Braun: 5−latek już dawno nie ma egzaminów wstępnych co jest największym błędem szkolnictwa. Niektóre osoby które dobrze napisały maturę, nie potrafią poradzić sobie z trudniejszymi zadaniami na analizie matematycznej czy algebrze. A czemu ? Odpowiedź jest prosta uczyły się schematów. Dlatego powinny powrócić egzaminy wstępne decydujące o dostaniu się na studia, a matura powinna być tylko jakby przepustką do tego egzaminu a nie decydować o dostaniu się na uczelnię !

Benny: W tym zad 6 jak wygląda ta druga nierówność?

5-latek:

	5
jest x*y+y≤9 i to samo dotyczy zdania nr 7 jest ≥		piszse takie zwroty bo jak uzywam
	2

tych z nakow z paska to potem z zllewa mi sie w jedna linijke

Benny: no to w 6 x=2

Benny: Zad 7 x∊(−1;3) ∪ (√2−1;+∞) /{0}

5-latek: Zaraz zobacze na odpowiedzi

5-latek: Nr 6 x=2 (czyli tak jak Ty Nr 7 Zalozenie −1<x<0 albo x>0 Zbior rozwiazan to {x:(0<x≤√2−1)⋁(x≥3)

5-latek:

	1
Odpowiedz do nr8 to T=		π
	3

Benny: coś w tym 7 musiałem, gdzieś źle zwrot zmienić

5-latek: Musisz poszukac sam bo jestem chory i nie chce wprowadzac blad (tak jak juz to dzisiaj zrobilem

Benny: Kurcze no nie wiem robię podstawienie, wychodzi mi x=3 lub x=√2−1 więc robię taki myk (x−3)(x−√2+1)≥0 i wychodzi mi z tego x∊(−1;0)∪(0;√2−1>∪<3;+∞)

	1
Wcześniej zrobiłem inaczej, bo miałem t1=		t2=2
	2

	1
zapisałem, że t∊(−∞;		>∪<2;+∞)
	2

	1
i rozwiązywałem logx+1 2 ≤		lub logx+12 ≥ 2 i z tego wyszedł mi ten przedział z
	2

13:54

Benny: Ktoś może to 7 przeanalizować?

Benny:

	π		π
a w ostatnim dochodzę do postaci y=|4sinx*sin(x+		)*sin(x−		)|
	3		3

Benny: Milu możesz przejrzeć? Oczywiście jak będziesz miała czas

Mila: W zadaniu 7 po zmianie podstaw:

log22(x+1)+1		5
	≥
log2(x+1)		2

Jeżeli (x+1)∊(0,1) to log₂(x+1)<0 Jeżeli (x+1)>1 to log₂(x+1)>0 Teraz rozwiąż dwie nierówności i wyjdzie jak w odpowiedzi.

Benny: Nie wiem co źle robię, ale nie wychodzi mi ten przedział (0;√2−1)

Mila: Poczekaj, po kolacji napiszę.

Benny: Chyba, że to będzie tak: 1)x>0

	5
log22(x+1)+1≥		log2(x+1)
	2

	1
(log2(x+1)−		)(log2(x+1)−2)≥0
	2

log₂(x+1)≤log₂√2 ∨ log₂(x+1)≥log₂4 x≤√2−1 ∨ x≥3 x∊(0;√2−1≥ ∪ <3;+∞) 2) x∊(−1;0)

	5
log22(x+1)+1≤		log2(x+1)
	2

	1
(log2(x+1)−		)(log2(x+1)−2)≤0
	2

log₂(x+1)≥log₂√2 ∧ log₂(x+1)≤log₂4 x≥√2−1 ∧ x≤3 x∊∅ więc x∊(0;√2−1≥ ∪ <3;+∞) ?

Mila: Zgadza się.

Benny: jak pisałem w zeszycie źle opuściłem logarytm stąd to zamieszanie

Benny: A ten zapis w kolejnym zadaniu możesz sprawdzić?

Mila: Zadanie 8 badaj z definicji: f(x+T)=f(x) To jest troche liczenia, ale wyszło mi T=2π.

Mila: Może PW podpowie inną metodę.

Benny:

	π
Odpowiedź do tego zadania podał wcześniej − 5−latek i T=
	3

	π		π
Dobrą drogą w ogóle idę jak mam y=|4sinx*sin(x+		)*sin(x−		)| czy może jakoś inaczej
	3		3

to zacząć?

5-latek: Odpowiedz do zadania jest taka (tez skorzystam z Waszych rozwiazan dana funkcja ze wzgledu na modul przyjmuje tylko wartosci nieujemne i jej wykres znajduje sie w I i II cwiartce ukladu wspolrzednych . Mozemy tu skorzystac z bezwarunkowej tozsamosci : sin3x=3sinx−4sin³x,czyli 4sinx³−3sinx=−sin3x mamy wiec (1) y=|4sin³x−3sinx|=|−sin3x| Z kolei zawazamy ze funkcja y=sinx ma okre T=2pi natomiast funkcja y=|sinx| przyjmuje tylko wartosci nieujemne wykonuja kolejne cykle swej zmiennosci 2 razy szybciej niz y=sinx wiec jej okres wynosi T=pi Ogolnie funkcje typu y=sinⁿ x maja okres podstawowy T=2pi gdy wykladnik n jest liczba

	1
naturalna nieparzysta a okres T=		*2pi=pi gdy n jest liczba naturalna parzysta
	2

Wreszczie dla wyznaczenia okresu badanej funkcji (1) uwzgledniamy ze funkcja typu y=sin l x

	2pi
gdzie l>0 ma okres T=		.
	l

	2
dlatego funkcje y=−sin3x i y=sin3x maja okresy T=		pi. Wiec nasza funkckja (1) ze wzgledu
	3

	1
na modul ma okres T=		pi
	3

Nie narysuje wykresu tej funkcji tutaj . Tyle co mam w odpowiedzi

5-latek: Ale jutro nastepne zadania bo dzisiaj juz jestem zmeczony

Mila: Znalazłam wzór na sin (3α) sin(3α)=3sinα−4sin³α W takim razie : |4sin3x−3sinx|=|sin3x|

	2π
Funkcja sin(ax) ma okres
	a

	2π
sin(3x) ma okres zasadniczy
	3

[ Umiesz to wykazać? sin[3*(x+T)]=sin(3x) ]

	2π		π
|sin(3x)| ma okres		=
	2*3		3

Mila: No to masz musztardę po obiedzie.

Mila: Załóż nowy wątek, bo trzeba długo przewijać stronę.

5-latek: Milu To nic w porownaniu gdzie Qulka piszse ponad 3100 postow

5-latek: Benny Mozesz wzor na sin3x sobie wyprowadzic sam znasz wzor na sin(x+y)=sinx*cosy+cosx*siny sin2x= sin(x+x) = sin3x=sin(2x+x) =