Symetralna odcinka AB
Kasia: Wyznacz równanie symetralnej odcinka AB jesli A=(4,7) B= (5,11)
Moja odpowiedź y= −1/2x+6 3/4
Proszę o weryfikację
8 mar 21:29
qulka:
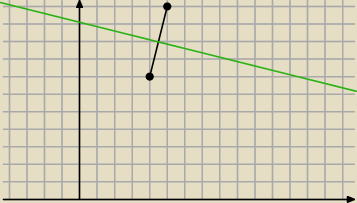
y=−x/4+81/8
8 mar 21:39
5-latek: | | 11−7 | |
wspolczynnik kierunkowy prostej AB a= |
| = 4 |
| | 5−4 | |
Wiec juz Twoja odpowiedz jest zla bo wspolczynnik kierunkowy a
1 symetralnej powinien wynosic
8 mar 21:39
Kasia: Policzyłam to tak:
A (4,7) B (5,11)
11=5a+b
7=4a+b
−−−−−−−−−−−
18=9a
2=a
11=5*2+b
1=b
y=ax+b
y=2x+1
Środek odcinka (4,5; 9)
y=−1/2x+b
9=−1/2*4,5+b
9=−2,25+b
6,75=b
y=−1/2x+6 3/4
8 mar 21:46
qulka: w pierwszym dodałaś więc 18=9a+2b a trzeba było odjąć
8 mar 21:48
8 mar 21:50
Kasia: Możesz mi to wytłumaczyć bo nie rozumiem do końca..
8 mar 21:51
5-latek:
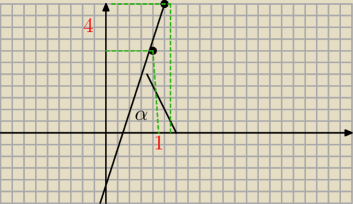
8 mar 21:54
qulka: Kasia..w pierwszym układzie odejmij stronami, a nie dodawaj
8 mar 21:55
5-latek: Wspolczynnik kierunkowy a prostej jest rowny tangensowi kąta α nachylenia prostej do osi OX
8 mar 21:56
5-latek: Dostalas link o 21:50 wiec licz z tego
8 mar 21:57
Kasia: Odjęłam i wyszło mi a=4 więc współczynnik odwrotny to właśnie −1/4
b= −9
po postawieniu do wzoru
y=−1/4x+b
9=−1/4*4,5+b
2,7=b
więc y= −1/4x+2,7
8 mar 22:01
qulka: 9− (−1.125) = 10.125
8 mar 22:07
5-latek: Kasia Rownanie prostej o znanym wspolczynniku kierunkowym a i przechodzacej przez punkt o
wspolrzednych (x
0 i y
0) jest takie
y=a(x−x
0)+y
0
S=(4,5 ,9) czyli x
0=4,5 i y
0=9
Podsatw do wzoru i licz
8 mar 22:07
Kasia: y= −1/4x + b
y=−1/4x + 10,125
8 mar 22:14
8 mar 22:22
Kasia: Całość ma wyglądać tak?:
A (4,7) B(5,11)
11=5a+b
7=4a+b
−−−−−−−−
4=1a odwrotność współczynnika a1 to −1/4
11=5*4+b
−9=b
Środek odcinka (4,5; 9)
Wzór symetralnej AB
1
y=−
(x −4,5)+9
4
1
y=−
x+1,125+9
4
1
y=−
x+10,125
4
8 mar 22:27
Kasia: Można prosić o potwierdzenie całości zadania ?
8 mar 22:45
8 mar 22:46
5-latek: 
8 mar 22:47
Kasia: Całość zapisu jest poprawna ?
8 mar 22:47
Qulka: może nie tyle odwrotność współczynnika, a raczej nazwać ..współczynnik prostej prostopadłej
bo on jest i odwrotny i przeciwny
8 mar 22:50
8 mar 22:51
Kasia: Wiem już o co chodzi, ale chciałabym wiedzieć czy w moim ostatnim długim poście to właściwe
rozwiązanie tego przykładu

8 mar 22:51
Qulka: reszta zapisu OK ( oprócz tego że ci koordynacja graficzna nie wyszła, ale sens i w zeszycie
będzie OK)
8 mar 22:51
Eta:
8 mar 22:53
Kasia: Dziękuję Wam Qulka i 5−latek i Eto(?).
Mam jeszcze pytanie odnośnie forum.
Czy można umieszczać pytania do dwóch różnych zadań w jednym temacie czy preferowane jest
tworzenie następnego?
8 mar 22:53
Eta:
Jak ich umieścisz za dużo,to .......... Ci napiszę,że nie chce mi się tyle czytać

8 mar 22:55
Kasia: Zaryzykuję

Wyznacz środek i promień okręgu
(x−7)
2+y
2=49 S (7,0) R= 7
(x−1)
2+(y−9)
2=100 S ( −1,9) R= 10
(x−1)
2+y
2=64 S (1,0) R= 8
x
2+y
2=3 S (0,0) R =
√3
8 mar 23:00
Eta:
1/ ok
2/ S(1,9)
3/ ok
4/ok
8 mar 23:05
Kasia: Dziękuję i dobranoc

"
8 mar 23:06
Eta:
Miłych snów

8 mar 23:08
 y=−x/4+81/8
y=−x/4+81/8





 Wyznacz środek i promień okręgu
(x−7)2+y2=49 S (7,0) R= 7
(x−1)2+(y−9)2=100 S ( −1,9) R= 10
(x−1)2+y2=64 S (1,0) R= 8
x2+y2=3 S (0,0) R = √3
Wyznacz środek i promień okręgu
(x−7)2+y2=49 S (7,0) R= 7
(x−1)2+(y−9)2=100 S ( −1,9) R= 10
(x−1)2+y2=64 S (1,0) R= 8
x2+y2=3 S (0,0) R = √3
 "
"
