funkcja
funkcja: Wyznacz wartosci parametru m dla ktorych dziedzina funlcji f jest zbior liczb rzeczywistych
Jak sie za to zabrac ?
16 lut 16:18
funkcja: odswiezam
16 lut 16:22
funkcja: pomoze ktos?:(
16 lut 16:26
J:
w mianowniku jest funkcja liniowa , aby nie przyjmowała wartości 0, musi być funkcją stałą,
czyli: m = 0
16 lut 16:27
funkcja: Dziekuje
moge pisac jakbym mial problemy z innymi zadaniami z f.wymiernej?
Planuje dzis posiedziec nad matmą.
16 lut 16:31
J:
tutaj zawsze znajdzie się ktoś, kto pomoże
16 lut 16:34
funkcja: Ok , cale zadanie mam dobrze zrobione z ta dziedzina.
Biore sie za kolejne
16 lut 16:38
funkcja: Wyznacz wartosci parametru m dla ktorych zbiorem rozw nierownosci jest przedzual (−2,0)
A) 6x<m
16 lut 16:43
Przemek: m>−3?
Tzn. głowy nie dam, ale podstawiłem to co jest poza granicą przedziału, a więc x=−2
i wziąłem, że to nie spełnia nierówności:
−3>m <−−−− wtedy nierówność nie jest spełniona
a więc m ma być większe niż −3, jeżeli nierówność jest spełniona
∞>m
i mniejsze od
∞
tak trochę na wyczucie
16 lut 16:52
funkcja: m=(−3) ma wyjsc. Mam pomysl zeby wykres narysowac i posprawdzac
16 lut 16:55
funkcja: Ciekawe czy jest jakis inny sposob na rozwiazanie
16 lut 16:58
Przemek: Ja źle zrobiłem z tym
bo:
16 lut 16:59
Przemek: Kurde, dobra kończę, bo nic nie pomogę, tylko się mylę
odwrotnie z tymi granicami, 1. −
∞, 2.
∞
Może bardziej ogarnięty się wypowie
16 lut 17:01
funkcja: Ok dzieki
16 lut 17:01
funkcja: Narysowalem wykres i nie wiem jak pozaznaczac te m
16 lut 17:04
J:
| | 6 | |
Narysuj sobie hiperbolę y = |
| .. przesuwaj linijkę równolegle do osi OX i patrz kiedy |
| | x | |
wykres leży nad linijką w zakresie x ∊ (−2,0)
16 lut 17:05
funkcja: Ok , robie tak i dojezdzam do punktu (−2,−3) i nie wiem czemu teraz ma m byc rowne −3 a nie
m<−3?
16 lut 17:19
J:
m < − 3 .. .wtedy w podanym przedziale: x ∊ ( −2,0) wykres leży nad linijką...
16 lut 17:21
funkcja: Jak to zrozumiem to tak jak poprzednie kazdy przyklad zrobie
16 lut 17:21
funkcja: Tego jalos nie rozumiem
ale kolejne 2 zad dobrze zrobione
16 lut 17:33
funkcja: Jak jest napisane ze 2 rozne pierwiastli to starczy Δ>0?
16 lut 17:43
J:
..tak, jeśli a przy x2 nie zalezy od parametru
16 lut 17:44
funkcja: Ok
16 lut 17:45
funkcja: Kolejne zadanie dobrze
szkoda ze tamto nie wyszlo
16 lut 17:51
funkcja: Ok teraz takie cos x2−2x−3x2+x−12≤0 zamienic na iloczyn ? I kiedy wgl mozna na taki
iloczyn zamienic?
16 lut 18:03
funkcja: Bo wychodzi mi w obu mirjsce zerowe 3
16 lut 18:10
funkcja: Odswiezam
16 lut 18:14
funkcja: Dobra nie bylo pytania , zapomnialem o dziedzinie
16 lut 18:16
funkcja: Wyznacz wartosci parametru m dla ktorych zbiorem rozw nierownosci jest przedzual (−2,0)
A) 6x<m : Dobrze, zrobilem wiele zadan i wracam do tego co nie zrobilem
moze teraz jakos to
zrozumiem. Moglbym prosic jeszcze raz o wyjasnienie krok po kroku?
16 lut 19:26
funkcja: Odswiezam...
16 lut 19:37
funkcja: .
16 lut 19:40
funkcja: ...
16 lut 19:46
funkcja: ....
16 lut 19:59
5-latek: Napisz jeszcze raz ale cale zadanie dokladnie
16 lut 20:12
funkcja: Wyznacz wartosci parametru m dla ktorych zbiorem rozwiazan nierownosci jest przedzial (−2,0)
A) 6x<m
16 lut 20:34
funkcja: .
16 lut 20:44
funkcja: ...
16 lut 20:51
funkcja: ....
16 lut 21:00
funkcja: ......
16 lut 21:07
funkcja: Kolejny dzien zadanek : tym razem :
Oblicz najmniejsza liczbe naturalna n spelniajaca nierownosc |3n+44n+5−34|<13600
17 lut 15:15
funkcja: Pomoze ktos?
17 lut 15:25
funkcja: Odswiezam
17 lut 15:33
Metis: Oblicz, a z otrzymanego przedziału wskaż najmniejszą liczbę naturalną...
17 lut 15:42
funkcja: Chcialem obliczyc ale mi Δ wyszla kilka milionow
17 lut 15:47
Metis: Gdzie tu funkcję kwadratową zauważasz O.o
17 lut 15:48
funkcja: Opuscilem wartosc i potem sie zrobila kwadratowa
17 lut 15:52
funkcja: Moze by tak narysowac wykres? Ale nie wiem czy to cos da , jesli mamy do czynienia z 13600
17 lut 15:53
Metis: Sprowadź do wspólnego mianownika.
| | a | | |a| | |
Skorzystaj z własności wartości bezwzględnej: | |
| | = |
| |
| | b | | |b| | |
Założenie ( mianownik ≠ 0)
Na krzyż.
Opuść wartość bezwzględną z koniecznym komentarzem: szukasz liczby naturalnej zatem n>0...
17 lut 15:55
funkcja: Ok sprobuje i zaraz dam znac jak wyszlo
17 lut 15:56
Metis: Opuścić wartość bezwzględna można zaraz po 1 kroku i nie bawić się z własnościami − skoro i tak
potem usuwamy moduł.
17 lut 15:59
funkcja: Pieknie
wyszlo 224 dziekuje za pomoc. A gdyby n nie bylo l. Naturalna ? To wtedy by trzeba
bylo wspolny mianownik i zmienic na iloczyn licznik i mianownik , tak?
17 lut 16:02
Metis: Tak jak poprzednio bez opuszczania wartości bezwzględnej... I potem 2 przypadki n>0 , n<0...
17 lut 16:07
17 lut 16:08
17 lut 16:11
funkcja: Tzn zmienil znak nierownosci
17 lut 16:12
funkcja: Czyli flatego,ze mniejsze od zera?
17 lut 16:13
funkcja: Dlatego* ze mniejsze od 0?
17 lut 16:14
Metis: Napisz, o który post Ci chodzi...
17 lut 16:18
funkcja: Pierwszy post Tadeusza
17 lut 16:18
funkcja: Dlaczego znak jest odwrocony w stosunku do tego , ktory byl w przykladzie?
17 lut 16:20
Metis: 5−latek ładnie Ci wyjaśnił...
17 lut 16:23
pigor: ..., zad. z 16.lut.20:34 ; wyznacz wartości parametru m
dla których zbiorem rozwiązań nierówności
6x<m jest przedział (−2,0)
−−−−−−−−−−−−−−−−−−−
np. tak : f(x)=
6x i f(−2)=
−3 =m − szukana wartość
m
możesz to sprawdzić rozwiązując nierówność
6x<−3. ...
17 lut 16:48
trapez: pigor, a dlaczego f(−2) ? bo jest skrajnym punktem przedziału ,a 0 nie mozna podstawić?
17 lut 18:32
pigor: ..., a czy możesz podstawić ; "podstaw" sobie i ...
co
widzisz
, ... nie należy do dziedziny funkcji f danej wzorem f(x)=
6x
17 lut 18:37
funckja : Ok, ja już to jakoś zrozumiałem
teraz spróbuję zrobić te nierówności z wartościami jeszcze
raz
17 lut 18:39
funkcja : Sorki ,że napisałem :funckja, ale na laptopa przeszedłem.
Nadal mam problem
x+2|x+2|<
2x−1
no i rozwiązuję następująco:
x>−2 :
x+2x+2<
2x−1
rozwiązuję i wychodzi
x∊(1,3)
x<−2
x+2−(x+2)<{
2x−1
rozwiązuję i wychodzi x∊(−1,1)
wiem, że gdzieś trzeba zamienić znaki, tylko nie wiem gdzie i czemu.
17 lut 18:50
17 lut 18:57
funkcja : dziękuję!
jakby co, tamte nierówności z 16 luty 20:34 także skończyłem. Zaraz biorę się za
te przykłady
17 lut 19:01
funkcja: Teraz troche inne ale nadal ten dzial
potrzebne do obliczenia q :
q=log
2 3 • log
3 8
17 lut 23:35
funkcja: Odswiezam
17 lut 23:43
funkcja: q=log
23*log
38=log
23*log
32
3=log
23*3log
32=
1log32*3log
32=
3*log32log32 =3
Udało się
17 lut 23:57
funkcja: Witam znow
Chcialem zapytac czy mozna narysowac wykres funkcji, gdy |x| jest w mianowniku poprzez rozbicie
jej na dwa przypadki : |x|=x dla x>0 i |x|= −x dla x<0 ?
Dokladny wykres to f(x)=
12|x|+2 −3
18 lut 16:57
funkcja: ..
18 lut 17:14
funkcja: ......
18 lut 18:14
funkcja: Albo jak najlatwiej ja narysowac? Pomijajac yo ,zeby to co po prawej na lewo a to co po lewej
znika? Chodzi mi o sposob z opuszcaniem wartosci bezwzglednej
18 lut 18:56
funkcja: I kolejne zadanie , w tym to nie wiem calkowicie o co chodzi :
Wyznacz wartosci parametru m, dla ktorych rownanie |x+3|=mm−4 ma dwa pierwiaski roznych
znakow ? ...
18 lut 19:10
funkcja: ....
18 lut 19:23
funkcja: .........
18 lut 19:36
prosta: | | m | | m | |
x+3= |
| lub x+3= − |
| |
| | m−4 | | m−4 | |
| | m | | m | |
x= −3+ |
| lub x= − 3− |
| |
| | m−4 | | m−4 | |
| | 12−2m | | 12−4m | |
x= |
| lub x= |
| |
| | m−4 | | m−4 | |
pierwiastki różnych znaków, więc ich iloczyn ma być ujemny
18 lut 19:46
5-latek: Post 16:57 tak jak piszsesz musisz zrobic
Rozpatrzyc te dwa przypadki
18 lut 19:48
funkcja: 5−latek cos mi nie wychodzi z tym rozbiciem bo wykres mi sie nie polaczyl w jeden ( przeaunalem
12−x ( x z przedzialu od −
∞,0) o wektor −2,3 i wychodzi ze nie sa polaczone. Asymptota w
x=2. Rysujac normalnie tzn odbijajac na lewo to co po prawej wychodzi ze polaczylu sie w
punkcie 0,3.
Zauwazylem ze gdyby przesunac o wektor 2,−3 to by wyszlo , tylko czemu tak?
18 lut 20:06
5-latek:
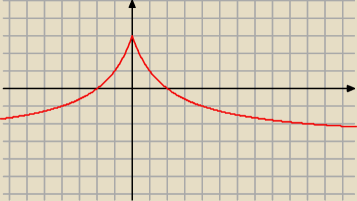
| | 12 | |
Taki jest wykres tej funkcji y= |
| −3 |
| | |x|+2 | |
18 lut 20:12
funkcja: Tak , tez go narysowalem ale sposobem to co po prawej na lewo, to co po lewej znika. Moglbys
pokazac jak robisz opuszczanie wartosci bezwzglednej?
18 lut 20:19
funkcja:
18 lut 20:34
funkcja: Ok, jak ktoś będzie to proszę o jakąś odpowiedź
18 lut 20:44
prosta:
| | 12 | |
f(x)= |
| −3 dla x<0 |
| | −x + 2 | |
| | − 12 | |
czyli f(x)= |
| −3 dla x<0 |
| | x − 2 | |
18 lut 20:49
funkcja: Aaaaa
dziekuje, juz wszystko wiadomo
18 lut 22:43
funkcja: Pora na trygonometrie
dlaczego cos(−690)=−
√3 2 jesli cos(k•360+α)=cosα
Wiec dlaczego nie dziala :cos(−690)= (−2•360+30 ) ≠ cos 30
Dlaczego sie nie rowna ?
20 lut 18:53
funkcja: I jak wgl liczyc sinusy cos, tg kątow mniejszych od zera?
20 lut 19:00
funkcja: Ehh znow sam sobie odpowiadam ...
cos(−α)=cosα
20 lut 19:03
funkcja: 90 nalezy do 1 czy 2 cwiartki?
26 lut 14:12
J:
ani tu ani tu , ruchome ramię kąta leży na granicy ( na dodatniej części osi OY)
26 lut 14:21
funkcja: Oblicz sin2x jesli sinx−cosx=√3−√22. Doszedlem do momentu cos(x+π/4)=√6−24 co
dalej?
26 lut 15:02
funkcja:
.....,.
26 lut 15:17
funkcja: Pomoze ktos?
26 lut 15:56
J:
| | √3 | | √2 | | √3 | | √2 | |
sinx − cosx = |
| − |
| ⇒ sinx = |
| i cosx = |
| |
| | 2 | | 2 | | 2 | | 2 | |
26 lut 16:07
funkcja: nie mozliwe ze tego nie zauwazylem.... Ehh wielkie dzieki
26 lut 16:16
funkcja: niestety przy takim zalozeniu wychodzi zly wynik
26 lut 16:26
J:
no racja .. to złe założenie
26 lut 16:31
funkcja: masz jeszcze jakis pomysl? Bo juz probowalem nawet z 1 tryg. To liczyc
26 lut 16:51
funkcja: Wszelkie nowe pomysly mile wodziane
26 lut 16:56
funkcja: To bylo takie banalne ze szkoda nawet to opisywac
26 lut 17:36
funkcja: Co zrobic jak wyprowadzilem wzor na sin(x+π/4)=1 a chce znac sin2x ? ( to juz inne zadanie )
26 lut 17:39
funkcja: ?
26 lut 18:22
prosta: ?
26 lut 18:26
prosta: a gdyby tak podnieść obustronnie do kwadratu?
26 lut 18:28
prosta: nie zwijać lewej strony do jednej funkcji
26 lut 18:29
prosta: sinxcosπ/4+cosxsinπ/4=1
sinx+cosx=√2
(sinx+cosx)2=2
26 lut 18:31
funkcja: Kolejne :
Czym roznia sie podane wzory:
2sinx2 2x oraz 2(sinx•cosx)2?
W pierwszym po uproszczeniu "2" jest w nawiasie i do kwadratu a w drugim nie jest? Prosze o
odpowiedz.
27 lut 18:39
funkcja:
27 lut 18:47
prosta: ten pierwszy po rozpisaniu ma współczynnik 8, ten drugi nadal 2
27 lut 18:59
funkcja: Moglbys rozpisac?
27 lut 21:30
funkcja: odswiezam
27 lut 22:19
funkcja: aaa ok mam
2*(2sinxcosx)
2 = 8sin
2xcos
2x
starczyło sekundę pomyśleć
27 lut 22:21
funkcja: Wykaz ze jesli a,b,c to kolejne wyrazy ciagu arytm. to 3(a
2+b
2+c
2)=6(a−b)
2+(a+b+c)
2
Pomocy:(
Wiem ze b=(a+c)/2 oraz a,a+r,a+2r to kolejne 3 wyrazy tylko nie wiem jak to wykorzystac
jak
robic tego typu zadania?:(
3 mar 20:52
funkcja: Pomoze ktos
3 mar 21:03
funkcja: :(
:(')
3 mar 21:12
3 mar 22:27
Qulka: podstawić zamiast b, c to a+r,a+2r i będziesz mieć jedno równanie w którym wszystko powinno
się skrócić
3 mar 22:29
funkcja: Rozumiem ,że rozpisać lewą stronę równania podstawiając odpowiednio a,a+r,a+2r i powinna wyjść
prawa strona?
3 mar 22:41
funkcja: ?
3 mar 22:48
Qulka: tak
3 mar 22:51
Qulka: tzn po bu stronach trzeba podstawić oddzielnie i doprowadzić do tego samego wyrażenia
3 mar 22:52
funkcja: |
a−bc+d| = |
b−ac+d|
7 mar 11:38
funkcja: ?
7 mar 11:47
funkcja: ?
7 mar 11:53
funkcja: Odpowie ktos?
7 mar 11:58
7 mar 12:14
funkcja: ...
7 mar 12:23
funkcja: Ile rozw ma rownanie 2x
3−x
2+x+5=0
7 mar 14:22
funkcja: ?
7 mar 14:50
funkcja: Pomoze ktos?
7 mar 15:10
7 mar 15:43
prosta: f(x)=2x3−x2+x+5
f'(x)=6x2−2x+1
Δ<0 ⇒f'(x)>0 dla x∊R
f jest rosnąca w zbiorze R ⇒jest różnowartościowa⇒ma dokładnie jedno miejsce zerowe
7 mar 15:54
prosta: Wielomian nieparzystego stopnia ma co najmniej jedno miejsce zerowe
7 mar 15:55
funkcja: jak rozpisac cos4x?
9 mar 22:02
funkcja: Ponawiam pytanie
10 mar 20:41
funkcja: ....... ...........
10 mar 22:02
funkcja:
11 mar 07:16
funkcja: Ponawiam to pytanie..... Jak rozpisac cos4x jak rozpisac cos(2*2x)...?
16 mar 19:10
funkcja: P(A|B)=2/3 P(B|A)=1/2 P(B)=1/2 oblicz P(A)
18 mar 08:54
funkcja: Czy zanjac czesc wspolna moge obliczyc P(A) odejmujac kolejno od 1 czyli omegi P(B) i dodajac
to co zostalo zabrane z P(A) pod odjeciu czyli P(Aczesc wspolnaB)
Robiac tak wyvhodzi mi 5/6
robiac normalnie 4/6 ... Co w tym sposobie co napisalem jest nie tak
18 mar 08:57
18 mar 09:09
funkcja: Pomoze ktos?
18 mar 09:38
funkcja:
18 mar 11:13
funkcja: ...?
18 mar 12:02
funkcja: ...?
18 mar 12:02
funkcja: ...?
18 mar 12:02
5-latek: Post 16.03 godz 19:10
cos 4x= cos(3x+x) i ze wzoru na cos(x+y)
lub cos4x=cos (2x+2x) i ten sam wzor
18 mar 12:08
5-latek: Zaloz nowy temat bo sie dlugo przewija
18 mar 12:08
J:
| | P(A*B) | | 2 | | 2 | | 2 | | 1 | | 1 | |
P(A/B) = |
| = |
| ⇔ P(A*B) = |
| *P(B) = |
| * |
| = |
| |
| | P(B) | | 3 | | 3 | | 3 | | 2 | | 3 | |
| | P(A*B) | | 1 | |
P(B/A) = |
| = |
| |
| | P(A) | | 2 | |
| | 1 | | 2 | |
P(A) = 2*P(A*B) = 2* |
| = |
| |
| | 3 | | 3 | |
18 mar 12:16