Wektor
Patryk: Witajcie, potrzebuje wytłumaczenia części zadania z wektorami.
Punkt C=(1, −3) jest wierzchołkiem trójkąta równobocznego ABC, zaś punkt S=(3,−1) jest środkiem
okręgu wpisanego w ten trójkąt. Wyznacz współrzędne wierzchołków A i B.
W rozwiązaniu jest (nie będę pisał strzałek nad literami):
K=(x
K,y
K) − punkt styczności okręgu wpisanego w trójką ABC z bokiem AB.
CS=[2,2]
SK=[x
K−3,y
K+1]
SK=0,5*CS=[1,1], zatem
x
K−3=1 ,y
K+1=1, stąd
K=(4,0)
Rysunek nie będzie konieczny, bo mam rozrysowane w zeszycie, ale chciałbym się dowiedzieć krok
po kroku jak to jest rozumowane (operacje na wektorach znam, ale nie potrafię ich użyć w
zadaniu
)
No i dalszą część zadania już bym rozwiązał.
9 lut 22:37
Qulka:
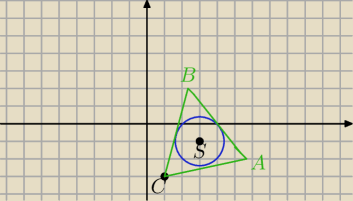
teraz np. AB ⊥ CK
9 lut 22:44
Patryk: Chodziło mi o wytłumaczenie wektorów, a nie co dalej
Ale... patrząc na pański rysunek zauważyłem, skąd jest wzięte 0,5*CS...
Czekałem ponad 2 godziny, aby ktoś zrobił rysunek (trochę lepszy od mojego
) i żebym sam
doszedł co i jak...
Dzięki Qulka
9 lut 22:48
Qulka: bo r wpisanego = 1/2 R opisanego = 1/3 h
| | a√3 | |
a dodatkowo h= |
| więc możesz wyliczyć a =2√6 |
| | 2 | |
9 lut 22:52
Patryk: Tak, tak, zauważyłem
Tylko na swoim rysunku nie robiłem nawet orientacyjnie boku AB, a tutaj wszystko widać, także
się kapnąłem o co chodzi
Jeszcze raz dzięki
9 lut 22:53
9 lut 22:56
Patryk: Pamiętałaś, ze coś takiego robiłaś?
Google mi nie wyszukało − słabo szukałem...
Dzięki
9 lut 23:07
Mila:
Dalej chcesz wektorowo?
9 lut 23:13
Patryk: Tzn to co napisałem wyżej mi wystarczy, tzn wyznaczenie punktu styczności.
A jest możliwość tego dokończenia za pomocą wektorów? jeśli tak, to chętnie, ale głównie mi
chodziło o dojście do tego K
9 lut 23:15
Mila:
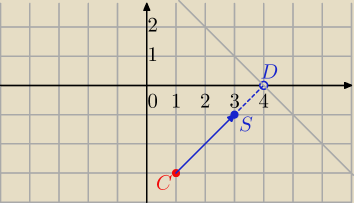
Punkt C=(1, −3) jest wierzchołkiem trójkąta równobocznego ABC, zaś punkt S=(3,−1) jest środkiem
CS
→=[2,2]
|CS|=2
√2=2r
S=(3,−1)→T{1,1]→=D(3+1,−1+1)=(4,0)− spodek wysokości Δ opuszczonej na AB.
AB⊥CD
AB⊥DS
Prosta AB:
SD
→=[1,1]
x+y+C=0
4+0+C=0
C=−4
AB: x+y−4=0
y=−x+4 na tej prostej leżą punkty A i B
Dalej sam.
9 lut 23:27
Patryk: Dzięki wielkie, już patrzę
9 lut 23:30
Mila:
9 lut 23:31
Patryk: Można tak?
y=−x+4
2√2=√(3−x)2+(−5 +x)2
9 lut 23:39
Patryk: Tzn za mało napisałem...
W sensie, że jest to |AS|, a |AS|=|CS|=2√2
9 lut 23:40
Mila:
Ja zrozumiałam Twój tok myślenia.
Tak może być, tylko ja piszę równanie okręgu tak:
(x−3)2+(y+1)2=(2√2)2
(x−3)2+(−x+5)2=8
9 lut 23:46
Patryk: Genialne
Ale to trzeba najpierw zauważyć, co mi się nie udało. No i oczywiście ułatwia trochę
To jeszcze raz dziękuję za rozwiązanie, zrozumiałem idee wektorów (na jakimś tam poziomie,
kosmosu to tutaj nie ma)
9 lut 23:51
Mila:
Cieszy mnie takie podejście do tego typu zadania. Na ogół wszyscy unikaja wektorów.
9 lut 23:53
bezendu:
Ja już nie unikam
9 lut 23:54
Mila:
Sesja zaliczona?
9 lut 23:55
Patryk: Jeszcze pytanie na szybko.
jak jest wyliczane C, do równania prostej AB.
mamy, że SD→=[1,1]
Więc równanie prostopadłe do tego wektora jest:
1*x+1*y+C=0, tak?
Wiem, że to od razu się pisze, ale chcę wiedzieć, czy to się wzięło z tego:
1214?
9 lut 23:55
Patryk: Chcę ogarniać te wektory, bo bardzo ułatwiają zadania z geometrii analitycznej (poziom: matura
rozszerzona
)
9 lut 23:56
Mila:
Do równania :
x+y+c=0 podstawiasz współrzędne punktu D (4,0) przez który ta prosta przechodzi.
9 lut 23:59
Mila:
DOBRANOC
10 lut 00:00
Patryk: Dziękuję, dobrej życzę
10 lut 00:01
bezendu:
Sesja już dawno zaliczona, od 28 stycznia mam już wolne średnia powyżej 5.0 wyszła ale nie będe
pisał bo wyjdzie, że się chwalę
10 lut 00:07
Patryk: Gratuluję
10 lut 00:12
Magik:
10 lut 00:15
Mila:
Gratulacje.
10 lut 17:24
bezendu:
Dziękuję, teraz biorę się za analizę 2, rachunek prawdopodobieństwa i analizę wektorową
10 lut 17:27