trójkąt
dawek: Punkt C=(1,−3) jest wierzchołkiem trójkąta równobocznego ABC, zaś punkt S=(3,−1) jest środkiem
okręgu wpisanego w ten trójkąt. Wyznacz współrzędne punktów A i B
18 sie 21:22
sushi_gg6397228:
rysunek zrobiony ?
18 sie 21:40
dawek: 2 punkty? ja mam na to sposób ale jest mega długi poza tym wychodzą mi pierwiastki i w miejscu
gdzie powinien wyjść 1 punkt wychodzą 2, czyli mam błąd.. Wektorów jeszcze nie miałem..
Mój sposób− punkt S to zarazem miejsce przecięcia wysokości, czyli odl z C do S to 2/3h.
policzę h, poprowadzę prostą CS i później policzę odl z S do D( wysokość z wierzchołka c)
podstawiając 1/3 wysokości.. później poprowadzę prostopadłą do CS przechodzącą przez punkt D i
policze A i B długość boku będę znał bo jak poprowadzę wysokość z C to mam trójkąt CAD i on ma
30 i 60 stopni, a długość h będe znał to oblicze długość boku

18 sie 21:48
dawek: ale za chiny mi nie wychodzi.. i nie mam błędu.. jest na to krótszy sposób?
18 sie 21:50
sushi_gg6397228:
Mozna policzyć |AS|= |CS| mając "h" policzyć długość boku "a" oraz |AC|= a
uklad rownan
lub próbować zrobić dokładny rysunek ( odmierzyć cyrklem CS, połowę CS i miec ) zrobić okąg i
poszukać A; B
18 sie 21:56
dawek: mam to wszystko obliczone.. jak to chcesz zrobić z układem..
18 sie 21:59
sushi_gg6397228:
(x−1)2+ (y+3)2= wpisujemy "a" podniesione do kwadratu
(x−3)2+ (y+1)2= wpisujemy długośc odcinka CS podniesiona do kwadratu
18 sie 22:14
sushi_gg6397228:
zrob rysunek i sprawdz swoje punkty
18 sie 22:15
dawek: w miarę optycznie pasuje.. Ale mógłbyś jeszcze pomóc rozwiązać ten układ. CS2=8 a a2=216
18 sie 22:31
dawek: mają wyjść jakieś dziwne liczby jak coś.
18 sie 22:31
Mila:
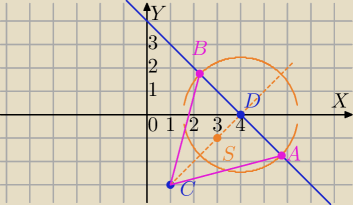
|CS|=
√22+22=2
√2
r=
√2
|CD|=h=3
√2
CS
→=[2,2]
SD
→=[1,1]
S=(3,−1)→[1,1]→D=(3+1,−1+1)=(4,0) −spodek wysokości opuszczonej na AB.
Prosta CD: y=ax+b,
0=4a+b
−3=a+b
a=1, b=−4
CD:
y=x−4
AB⊥CD
AB: y=−x+b i prosta przechodzi przez punkt D
0=−1*4+b, b=4
y=−x+4
Kreślimy okrąg o środku w Punkcie D i R=
√6, punkty A i B to punkty przecięcia z prostą y=−x+4
Algebraicznie :
(x−4)
2+y
2=6
y=−x+4
(x−4)
2+(−x+4)
2=6⇔
2*(x
2−8x+16)=6 /:2
x
2−8x+16=3
x
2−8x+13=0
Δ=64−52=12,
√12=2
√3
x=4−
√3 lub x=4+
√3
y=−(4−
√3)+4=−4+
√3+4
B=(4−
√3,
√3)
A=(4+
√3,−
√3)
Czy takie masz odpowiedzi, bo mogłam się pomylić w rachunkach, albo przepisywaniu.
18 sie 23:53
Eta:
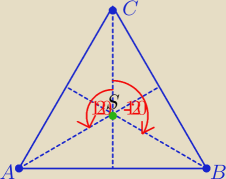
C(1,−3) , S(3,−1)
Obracając punkt C dookoła punktu S o kąt 120
o otrzymamy punkt A
Obracając punkt C dookoła punktu S o kat −120
o otrzymamy punkt B
Równanie obrotu:
x'=(xC−xS)*cosα−(yC−yS)*sinα+xS
y'=(xC−xS)*sinα +(yC−yS)*cosα +yS
| | 1 | | √3 | | 1 | |
cos120o= − |
| , sin120o= |
| , cos(−120o)= − |
| , |
| | 2 | | 2 | | 2 | |
| | 1 | | √3 | |
A: x'=−2*(− |
| )+2* |
| +3 ⇒ x'=4+√3 |
| | 2 | | 2 | |
| | √3 | | 1 | |
y'=−2* |
| −2*(− |
| )−1 ⇒ y'= −√3 |
| | 2 | | 2 | |
A(4+√3, −√3)
| | 1 | | √3 | |
B: x'=−2*(− |
| −2* |
| +3 ⇒ x'=4−√3 |
| | 2 | | 2 | |
| | √3 | | 1 | |
y'= −2*(− |
| )−2*(− |
| −1 ⇒ y'= √3 |
| | 2 | | 2 | |
B(4−√3, √3
18 sie 23:53
Eta:

18 sie 23:55
Mila:
Puk, puk nasze szczęscie , o jednej godzinie i minucie wpisane.
18 sie 23:58
Eta:
Witaj
Mila 
Co tak pozieleniałaś ?

19 sie 00:02
Mila:
Zielone liście lata. Witam miło.
19 sie 00:04
Eta:

19 sie 00:06
daras: a u mnie liście już żółkną
19 sie 10:55
dawek: dzięki

juz wiem, dlaczego mi nie wychodziło

pieprznołem się na począdku w rachunkach

19 sie 12:53
Mila:
Nie wyrażaj się brzydko, to jest elitarne forum.
19 sie 15:22
daras: zamiast pierzników wstawiamy ...

19 sie 15:44
pigor: ... a do swojej szuflady krótko np tak:
A=(x,y), B=(x,y)=?
1) C=(1,−3), S=(3,−1) ⇒ |CS|=
√4+4=
√8=2
√2 i
D==(3+1,−1+1)=
(4,0),
(*) (x−3)2+(y+1)2= 8 równanie
okręgu opisanego na ΔABC;
−−−−−−−−−−−−−−−
2) równanie prostej CS≡CD:
12(x−1)=
12(y+3) ⇔
x−y−4
to równanie prostej AB: ⊥CS przez D 1(x−0)+1(y−4)=0 ⇔ x+y−4=0 ⇒
⇒
(**) AB: y=4−x
−−−−−−−−−−−−−−−−−−−−
3) z układu równań
(*) i (**) y=4−x i (x−3)
2+(5−x)
2=8 ⇒ 2x
2−16x+26=0 ⇔
⇔ x
2−8x+16−3=0 ⇔ (x−4)
2=3 ⇔ |x−4|=
√3 ⇒
x=4±√3 i y=4−(4±√3) ⇒
⇒
A=(4+√3,−√3) i B=(4−√3,√3) albo odwrotnie . ...

19 sie 19:01
Eta:
Ja wolę "coś" ze ...
swoiej szufladki 
19 sie 20:15

 |CS|=√22+22=2√2
r=√2
|CD|=h=3√2
CS→=[2,2]
SD→=[1,1]
S=(3,−1)→[1,1]→D=(3+1,−1+1)=(4,0) −spodek wysokości opuszczonej na AB.
|CS|=√22+22=2√2
r=√2
|CD|=h=3√2
CS→=[2,2]
SD→=[1,1]
S=(3,−1)→[1,1]→D=(3+1,−1+1)=(4,0) −spodek wysokości opuszczonej na AB.
 C(1,−3) , S(3,−1)
Obracając punkt C dookoła punktu S o kąt 120o otrzymamy punkt A
Obracając punkt C dookoła punktu S o kat −120o otrzymamy punkt B
Równanie obrotu:
x'=(xC−xS)*cosα−(yC−yS)*sinα+xS
y'=(xC−xS)*sinα +(yC−yS)*cosα +yS
C(1,−3) , S(3,−1)
Obracając punkt C dookoła punktu S o kąt 120o otrzymamy punkt A
Obracając punkt C dookoła punktu S o kat −120o otrzymamy punkt B
Równanie obrotu:
x'=(xC−xS)*cosα−(yC−yS)*sinα+xS
y'=(xC−xS)*sinα +(yC−yS)*cosα +yS

 Co tak pozieleniałaś ?
Co tak pozieleniałaś ? 

 juz wiem, dlaczego mi nie wychodziło
juz wiem, dlaczego mi nie wychodziło pieprznołem się na począdku w rachunkach
pieprznołem się na począdku w rachunkach 


