1 lut 19:04
Hajtowy: nie ładnie
1 lut 19:07
Hugo: Dana jest forma kwadratowa g(x) = x
1x
2 −x
1x
3 −2x
23 m E
3 i f(x) = x
1x
2 − x1x3 −
| | 2 | |
2x |
| − 4x1x4 + 2x2x4 w E4 |
| | 3 | |
a) Zapisz macierz Grama formy f(w bazie standardowej);
b) Sprowadź formę g do postaci kanonicznej
1 lut 19:07
Hugo: jest troche nie czytelnie prosze o weryfikacje
1 lut 19:07
Hugo: poprawiam
Dana jest forma kwadratowa g(x) = x1x2 −x1x3 −2x23 w E3 i f(x) = x1x2 − x1x3 −
2x23 − 4x1x4 + 2x2x4 w E4
a) Zapisz macierz Grama formy f(w bazie standardowej);
b) Sprowadź formę g do postaci kanonicznej
1 lut 19:09
1 lut 19:11
1 lut 19:13
Eve: w 6 może to byc przestrzeń współrzędnych
1 lut 19:18
Hugo: juz czytam : )
1 lut 19:24
Eve: wydaje mi sie, że przestrzeń funckji prawie okresowych też jest nieskończenie wymiarowa, ma
nieskończoną bazę
1 lut 19:40
Gray: Co to jest przestrzeń współrzędnych? Najlepsze są najłatwiejsze przykłady: przestrzeń
wielomianów, przestrzeń funkcji ciągłych, przestrzeń ciągów zbieżnych do zera, itd, itp.
1 lut 19:52
Hugo: Ogarniam ten pierwszy link i fajne
metoda sarrusa mi sie coś nie zgadza ale no chodzi o
metode : > A jest ktoś tu kto planuje siedzieć do ~0:00?
1 lut 19:54
Draghan: Ja zamierzam i dłużej, ale pewnie nie będę umiał Ci pomóc.
1 lut 19:56
Eve: ja tam nie wiem co teraz na studiach żądają, może jakieś nietrywialne przykłady
miałam na
myśli przestrzeń wektorową o wektorach "nieskończonych"
1 lut 19:57
Gray: R
∞
1 lut 20:13
Eve: K∞, x=(x1,x2,x3,x4,...) mam nadzieję, że dobrze
1 lut 20:15
Hugo: Ogarnąłem troszke i spróbuje z3 a o co chodzi z tym diagolizowalna
2..0..3
0.−1..0
3..0..2
L − lambda
det ( A − LI) =
2..0..3 L..0..0
det( 0.−1..0 − 0..L..0 )
3..0..2 0..L..0
z Sarrusa
2−L .. 0 .. 3
0.....−1−L..0
3......0.....2−L
2−L .. 0 .. 3
0.....−1−L..0
(−1−L)[−9+(2−L)2]
(−1−L)[ L2 −2L −5]
Δ = 24 −,− ?!?! to dobrze robie? ...
1 lut 20:53
Eve: dobrze
1 lut 21:05
Eve: tylko w drugim nawiasie: [(2−L)2−9]=(2−L+3)(2−L−3)
1 lut 21:06
Eve: jesli wartości własne są jednokrotne, to jest diagonalizowalna, jeśli nie to nie jest
1 lut 21:10
Hugo: ze jak jest x =1 , x = 2, x = 3 to są?
a jak jest x = 1 , x = 2 , x = 2
x = 3 to jak podwójnie dwa to nie jest?
1 lut 21:32
Gray: Oj, mogą wartości własne być wielokrotne i może być diagonalizowalna.
1 lut 21:33
Gray: W Twoim przypadku właśnie wartości własne to λ1=λ2=−1, λ3=5, a jest diagonalizowalna.
1 lut 21:37
Hugo: czyli delta dobra?
to liczyc dalej?
takie ma wyjść ;−;
!?!
1 lut 21:37
Eve: tzn? wystarczy żeby wektory własne tworzyły bazę?
1 lut 21:39
Hugo: Gray
co z rozwiązaniami
? delta 24 więc to sie słabo pieriwastkuje
z pierwszego nawiasu mam L = −1 to czemu mi nie wychodzi L
2 = 5 v L
3 = −1 ?!?!?
1 lut 21:39
Eve: Hugo nie przeczytałes mojego postu z 21.06
1 lut 21:39
Gray: Dla każdej wartości własnej musi się udać znaleźć tyle wektorów własnych liniowo niezależnych,
ile wynosi krotność tej wartości własnej jako pierwiastka wielomianu charakterystycznego. To
m.in. oznacza, że wektory własne utworzą bazę całej przestrzeni.
1 lut 21:41
Hugo: przeczytałem
1 lut 21:42
Gray: Zamiast z delty odpalać weź a2−b2=(a−b)(a+b).
Źle sobie wymnożyłeś to i delta wyszła jaka wyszła.
1 lut 21:42
Hugo: zgubułem −2L
no !
1 lut 21:46
Hugo: no dobra to mamy
L = −1
L = −1
L = 5
i teraz: pokolej
2..0..3 −1..0..0
0.−1..0 − 0..−1..0 =
3..0..2 0..0..−1
3..0..3 x
1 0
0..0..0 x
2 0
3..0..3 x
3 0
3x
1 + 3x
3 = 0
3x
1 + 3x
3 = 0
x
1 = −x
3
a x
2 jest nie oznaczony
? nie wiem co wpisać
−x
3 np −1
? ?
x
3 1
1 lut 21:52
Eve: Gray czyli diagonalizowalność zależy od wektorów, nie od wartości własnych?
1 lut 21:53
Eve: zapisz x2 za pomocą x3
1 lut 21:53
Eve: x2 może byc dowolny
wektor własny [−x3,0,x3] np
1 lut 21:56
Gray: Nie, najpierw wartości własne, potem wektory. Ten wektor własny jest postaci [−x3,x2,x3].
Czyli możemy wybrać dwa liniowo niezależne, np. [−1,0,1] i [0,1,0], więc macierz jest
diagonalizowalna.
1 lut 21:58
Gray: Eve, diagonalizowalność zależy od tego i od tego.
1 lut 22:00
Eve: o to mi właśnie chodziło
1 lut 22:00
kyrtap: Gray jakie książki jadłeś jak studiowałeś?
1 lut 22:00
Eve: dzięki, kiedyś algebrę miałam w małym palcu, trochę się zapomniało
1 lut 22:01
Hugo: nie rozumiem
to co powinienem napisać podstawiłem pod x
1 = x
3 i tu jest jedna zmienn a x
2
co z nim napisać?
1 lut 22:01
1 lut 22:03
Eve: znalazłeś wektory własne, one nie zawsze sa liczbami, możesz wybrać z tych [−x3,x2,x3]
1 lut 22:03
Gray: Rozwiązując układ otrzymałeś, że x1=−x3, a na x2 nie miałeś żadnego warunku. No więc x2
może być dowolne; stąd postać [−x3,x2,x3]. Uwaga: wektor [0,0,0] nie jest wektorem własny,
więc x2 i x3 nie mogę być jednocześnie zerami.
1 lut 22:04
Gray: Oj,
kyrtapie Drogi, zdziwiłbyś się. Uwielbiam Thorgale
(stare)
1 lut 22:06
Hugo: Gray dziękuję o to mi chodziło
1 lut 22:10
kyrtap: To poleć Mi mój Mentorze drogi jakieś
1 lut 22:16
Hugo: i teraz sprawdzało się dla drugiego
L = 5
2..0..3 5..0..0
0.−1..0 − 0..5..0 =
3..0...2 0..0..5
−3..0..3
0..−6..0
3...0..−3
1 lut 22:19
Hugo: −3..0..3 x
1 0
0..−6..0 x
2 0
3...0..−3 x
3 0
−3x
1 + 3x
3 = 0
−6x
2 = 0
3x
1 −3x
3 = 0
x
2 = 0
x
1 = x
3
zatem:
x
1
0
x
1
i jaki powinien być komentarz?
1 lut 22:21
Eve: [1,0,1]
1 lut 22:22
Hugo:
1 lut 22:29
Hugo: ok
które mógłbym zrobić z wami kolejne zadanie?
1 lut 22:29
Hugo: Czy drugie to jakaś teoria?
1 lut 22:29
Eve:
warunkiem koniecznym i wystarczającym na to, aby macierz o wymiarach nxn była diagonalizowalna
jest istnienie bazy w Rn złożonej wyłącznie z wektorów własnych tej macierzy
1 lut 22:38
Hugo:
Eve które mogła byś ze mną zadanie przerobić?
1 lut 22:40
Eve: co do 4, wydaje mi sie, że chodzi o macierze ortogonalne, chodzi o zachowanie odległości
punktów
1 lut 22:43
Eve: z tego linku z 22.03?
1 lut 22:44
Hugo: : > to spróbujmy to zadanie 4 z egzaminu, co do linku 22.03 ja tam powoli ogarniam ale i tak
nie rozumiem −,−
1 lut 22:51
Hugo: powiedz mi jak sie zabrać
1 lut 22:51
Hugo: jakie macierze odpowiadają izometriom przestrzenio En ? Opisz własności takich macierzy
1 lut 22:52
Eve: dla tych macierzy ortogonalnych sa własności
det(AAT) = det A*det(AT),
det A*det(AT) =det I = 1,
det(AT) =det A⇒ (det(A))2 = 1
1 lut 22:57
Eve: liniowość sprawdzasz na zasadzie addytywności i mnożenia przez skalar
f(x+y)=f(x)f(y)
αf(x)=f(αx)
wszystko opiera się na przekształceniach
1 lut 23:00
Gray: Macierze izometrii to macierze ortogonalne (w przypadku rzeczywistym), tj. A
TA=I.
Macierze takie zachowują długość, tj. ||x||=||Ax|| → stąd właśnie się tu biorą. Własności mają
sporo, poczytaj np. na wiki
http://pl.wikipedia.org/wiki/Macierz_ortogonalna
1 lut 23:00
Eve: ufff, dobrze pamiętam
1 lut 23:04
1 lut 23:10
Eve:
6. Bazą przestrzeni liniowej P nazywamy zbiór V wektorów tej przestrzeni, taki że :
V generuje całą przestrzeń P tj. lin V = P
V składa się z wektorów liniowo niezależnych.
wymiar P:
Liczbę elementów dowolnej skończonej bazy przestrzeni liniowej P nazywamy
wymiarem przestrzeni P i oznaczamy przez dim P .
1 lut 23:15
Eve: powodzenia jutro
Hugo pochwal się 5
1 lut 23:45
Hugo: zeby 3
1 lut 23:53
Draghan: Będzie dobrze.
2 lut 00:42
Hugo: pytanie jak przemnożyć wektory
2 lut 00:47
Hugo: [2,0,1,1]
o [1,1,1,1]
2 lut 00:48
Hugo: dobra nie bylo pytania
2 lut 00:50
Hugo: a
mam pytanie
2 lut 01:17
2 lut 01:18
2 lut 08:17
Gray: Masakra w tym linku
To jest bardzo proste. Omówię na przykładzie.
Rozważmy formę kwadratową f(x
1,x
2,x
3)= x
12+2x
1x
3 + 4x
1x
2+ 2x
22 − 3x
32.
Macierz tej formy tworzymy tak: oznaczmy ją jako A=[a
ij]. Wówczas
a) elementy na przekątnej a
ii to współczynnik przy x
i2; w tym przypadku mamy więc:
a
11=1, a
22=2, a
33=−3
b) macierz ma być symetryczna więc elementy a
ij i a
ji muszą być równe − każdy z nich to
połowa współczynnika stojącego przy x
ix
j.
W rozważanym przypadku: a
12=a
21=2, a
13=a
31=1; a
23=a
32=0.
Ostatecznie:
A=
1 2 1
2 2 0
1 0 −3
2 lut 08:27
Hugo: nie rozumiem Gray
2 lut 08:47
Hugo: co to aii , aij
2 lut 08:48
Hugo:
Okej czyli przekątna to są przy x
1
2 lut 08:52
Hugo: 1, 2 −3
bo
x12 + 2x1x3 − 3x32
2 lut 08:53
Eve: weź sobie to tak:
w twojej formie masz a11 stoi przy x1, a12 stoi przy x1x2 itd
2 lut 08:59
Hugo: ale no hmm
2 lut 09:00
Hugo: a możesz to dokończyć tzn:
a
11 = to co przy x
1
a
12 = to co przy x
1x
2 ale przez dwa chyba
?!?!
a
13 =
?
a
32 =
?
2 lut 09:02
Eve: ja to zrozumiałam tak:
na przekątnej piszesz współczynniki stojące przy x1, x2 i x3
Gray napisał, że macierz ma być symetryczna, więc kolejne wyrazy muszą być równe
czyli ten przy x1x2=x2x1=4 x1x3=x3x1=2, x2x3=x3x2=0
i bierzemy połowę tych współczynników
2 lut 09:18
Hugo: not tak na przekątnej tak
2 lut 09:29
Hugo: ale skąd mam wiedzieć jakie wyrazy i w które miejsce do tego roku
?
2 lut 09:30
Eve: przetraw to co napisałam dalej
2 lut 09:31
Hugo:
skąd mam wiedzieć jakie wartości tu podawać
powiedzcie mi , współczynniki przy jakich 'x' w
które miejsce
2 lut 09:31
Hugo: wiem ze przekątna i wiem ze symetrycznie ale to moje
2 lut 09:32
Eve:
współczynnik przy x1x2=4, więc a12=a21=2, przy x1x3=2, więc a13=a31=1
przy x2x3=0, więc a23=a32=0
2 lut 09:38
Hugo: rozumiem xd
2 lut 09:43
Eve: a u ciebie jest :
x1x2=0, więc a12=a21=0
x1x3=2, więc a13=a31=1
x2x3=4, więc a23=a32=2
stąd macierz B
2 0 1
0 1 2
1 2 3
2 lut 09:44
Hugo:
2 lut 09:45
Eve: chodzi ci o to gdzie są te a12 i a 23?
pierwsza liczba to wiersz, druga to kolumna
2 lut 09:46
Gray: Dokładnie tak. Indeksy przy x pokazuję gdzie pakujesz w macierz: x12 = x1x1 więc stoi na
miejsc 11 − pierwszy wiersz, pierwsza kolumna ← tak na przekątnej.
Współczynniki np. przy x1x2 muszą wypełnić miejsca 12 i 21 (pierwszy wiersz druga kolumna i
drugi wiersz pierwsza kolumna), ale aby macierz była symetryczna dzielimy go na pół. Itd.
2 lut 09:48
Hugo: o to mi chodziło xd przez dłuższy czas, DZIĘKUJE WAM !
2 lut 09:55
Eve:
2 lut 09:56
2 lut 09:57
Hugo: z2. jak sformuować?
2 lut 09:57
Eve: patrz 22.38
2 lut 09:59
Hugo: i to z 22:38 jest wystarczające ? : ))
2 lut 10:04
Eve: taki znalazłam
2 lut 10:05
Hugo: Hmm a co do zadania 4
2 lut 10:07
Hugo: Jakie macierze odpowiadają izometriom przestrzeni E
n? Opisz wlasności takich macierzy?
który to był post czu cuś
2 lut 10:08
Eve:
22.57 i 23.00
2 lut 10:09
Hugo: I jak mu to zapisze to bedzie zaliczone czy to to jeszcze jakoś mu coś rozpisywać?
2 lut 10:15
Eve: możesz napisać co to jest macierz ortogonalna, to się ucieszy
2 lut 10:16
Hugo: oK
2 lut 10:18
Hugo: metoda ortogonalizacji grama schmidta sprowadź układ wektorów U = }(1,0 − 1,,0) ,
(1,−1,
1, −1) , (−3,2, −3, 0} w przestrzeni euklidesowej E
4 do układu ortogonalnego V
te na czerwono wymyslilem bo nie widać
2 lut 10:18
Eve:
23.10
2 lut 10:20
2 lut 10:20
Hugo: TAK
masz racje patrzyłem tam
nawet juz sb wpisałem wzór do karty z wzorami
Eve: Zakladam ze jesteś po studiach? albo gdzieś tam już wyżej niż na 1 roku, jak wyglądało u
cb "kartka ze wzorami" u nas na WIKI piszą ze to nie sprawdzają można wlepiać co sie da i
pytanie ile można miec kartek ze wzorami
2 lut 10:21
Hugo: 
tyle ze w tym linku 23:10 jest R
2 .. daj chwile ogarne
2 lut 10:22
Eve: Hugo jak ja kończyłam studia, to coś takiego jak karta wzorów nie istniała
trza było mieć wszystko w głowie
2 lut 10:32
Eve: ten ostatni link masz fajny, wszystko widać krok po kroku
2 lut 10:35
Hugo: Dziś o 16 pisze : / w Środe fizyke, w Czw analize + infe o ile zdałem , w pt chemie
2 lut 10:49
Eve: współczuję
2 lut 10:53
Hugo: myślałem ze napisze "Będzie dobrze Hugo, może teraz nic nie umiesz ale są jeszcze dwa terminy
"
wzór do orto.. na R
3
| | v3 ou1 | | v3ou2 | |
v3 = v3 − |
| o u1 − |
| o u*2 |
| | u1ou1 | | u2ou2 | |
2 lut 11:01
Hugo: to próbuje:
2 lut 11:01
Eve: ależ dobrze będzie, trzeba myśleć pozytywnie
2 lut 11:08
Hugo: metoda ortogonalizacji grama schmidta sprowadź układ wektorów U = }(1,0 − 1,,0) ,
(1,−1, 1, −1) , (−3,2, −3, 0} w przestrzeni euklidesowej E4 do układu ortogonalnego V
zatem mamy:
v
1 = u
1 = (1, 0, −1, 0)
v
2 = (1,−1,
1, −1)
v
3 = (−3, 2, −3, 0)
| | v2* u1 | |
u2 = v2 − |
| * u1 |
| | u1*u1 | |
pomocnicze
u
1 * v
2 [1, 0, −1, 0] * [1,−1, 1, −1] = 1 + 0 − 1 + 0 = 0
u
1 * u
1 = [1, 0, −1, 0] * [1, 0, −1, 0] = 1 + 0 + 1 + 0 = 2
dobrze
To sie góra zeruje w liczniku
u
2 = v
2 − 0 * u
1
u
2 = [1,−1, 1, −1]
?
2 lut 11:10
Hugo: ~ TO nie imagination world ... Uderzyła do mnie Rzeczywistość
~
− Hugo
2 lut 11:12
Eve: dobrze, tez mi sie wyzerowała
2 lut 11:13
kyrtap: Hugo po ci chemia na infie?
2 lut 11:14
Hugo: chemia jest wszędzie
....
Eve
no dobrze i co z tym sie dalej robi? tworzymy u
3 tak?
2 lut 11:16
Hugo: | | v3 * u1 | | v3 * u2 | |
u3 = v3 − |
| * u1 − |
| * u2 |
| | u1 * u1 | | u2 * u2 | |
2 lut 11:18
Eve: tworzymy u3
2 lut 11:18
Hugo: | | v3 * u1 | | v3 * u2 | |
u3 = v3 − |
| * u1 − |
| * u2 |
| | u1 * u1 | | u2 * u2 | |
u
1 = [1, 0, −1, 0]
u
2 = [1,−1, 1, −1]
v
3 = [−3, 2, −3, 0]
u
1 * v
3 = −3 + 0 +3 + 0 = 0 XDDDDDDDD czo otototottototo ?~!
licze v3 * u2
u
2 = [1,−1, 1, −1]
v
3 = [−3, 2, −3, 0]
v
3 * u
2 = −3 −2 −3 + 0 = −8
u1 * u1 = 2 //z tamtego postu
u
2 * u
2 = 1 +1 + 1 + 1 = 4
| | v3 * u1 | | v3 * u2 | |
u3 = v3 − |
| * u1 − |
| * u2 |
| | u1 * u1 | | u2 * u2 | |
| | 0 | | −8 | |
u3 = v3 − |
| u1 − |
| * u2 |
| | 2 | | 4 | |
u
3 = [−3, 2, −3, 0] +2 [1,−1, 1, −1]
u
3 = [−3, 2, −3, 0] + [2,−2, 2, −2]
u
3 = [−1, 0, −1, −2]
2 lut 11:27
Eve: sie mi też wyzerowało
i reszta ok
2 lut 11:29
Hugo: 1. i co teraz sie liczy?
jaki komentarz? ; ( bo nie wiem co
2. Co do zadania 6 co bys radziła
?
3. naucz mnie jeszcze prosze z kwadratowej −> kanoniczną i w drugą stronę
2 lut 11:32
Eve:
do 6 23.15 i 19.52
2 lut 11:36
Eve: liczymy normę wektorów
2 lut 11:39
Hugo: co to norma wektorów
2 lut 11:40
Hugo: no dobra
R3 = √ x1 + y2 + z2
2 lut 11:43
Hugo: i co później
?
2 lut 11:43
2 lut 11:48
Eve: wyznaczamy bazę ortonormalną, tak jak masz w linku
norma wektora: IIvII=√v*v(kolumnowy)
2 lut 11:50
Eve: mam wrażenie, że ja stąd wcale nie poszłam od wczoraj
2 lut 11:53
Hugo: baza ortogonalna czyli to
| | ,,, | |
u2 = v2 − |
| u1 tak? |
| | ,,, | |
i co gdzie podstawić
?
prosze rozpisz mi to w linku patrzyłem jest dla mnie średnio zrozumiałe
2 lut 11:58
Hugo: co to v(kolumnowy?)
2 lut 12:00
Eve: wektor zapisany jako kolumna
2 lut 12:03
Eve: masz u1, u2, u3, policz ich normę
2 lut 12:05
2 lut 12:12
Hugo:
2 lut 12:13
Hugo: tak
?
2 lut 12:13
Eve: nie, IIu1II=√(1,0,−1,0)(i teraz kolumna z u1)=
2 lut 12:14
Eve: albo prościej
√12+02+(−1)2+02
2 lut 12:17
Eve:
IIu
1II=
√2
IIu
2II=2
IIu
3II=
√6
teraz baza ortogonalna:
i zapomnieliśmy o u
4
2 lut 12:26
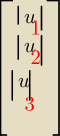
Hugo: wiec
Il u
1 ||
a czemu sie nie pisze |u
1|
?
Il u
1 || =
√2 * jak operować na tej kolumnie?
Il u
1 || =
√2 [1,0,−1,0]?
2 lut 12:27
Eve: bo Iu1I to wartość bezwględna , tak coby nie pomieszać tych pojęć
2 lut 12:30
Hugo: bo ja rzuciłem hasło kanoniczna −> kwadratowa i w II strone
a wartości do przykładów skąd pobierasz?
2 lut 12:30
Hugo: || u1 || to nie wartość bzwględna?
2 lut 12:31
Eve: nie, bo to wektor a nie liczba i IIuII oznacza długość
2 lut 12:33
Eve: z wujka googla
2 lut 12:33
2 lut 12:34
Eve: ortogonalizacje mamy z głowy, tylko tam jeszcze powinien byc wektor u4 znaleziony, bo teraz
mamy bazę 3 elementową, a przestrzeń E4
2 lut 12:35
Eve: no jest, ale po co się tak męczyć, wyjdzie to samo
2 lut 12:36
Hugo: jak znaleźć u4 ?
wzór co tego korzystałem to
U4 − v4 a v4 nie ma
2 lut 12:39
Kamil: hahaha o ja jebe xD wchodzę na matematyka pisz a tu mój kierunek się uczy xD Pozdrawiam IS, i
powodzenia dziś
2 lut 12:46
Hugo:
czyli jak jest norma wektorów pod pierwiastkiem to sie sie oblicza:
√ x*x + y*y + z*z) tak?
2 lut 12:49
Hugo: Ahoj ____________ ale tu chyba nas więcej bedzie
2 lut 12:49
Eve: tak
a nam u
4 nie potrzebne, bo mi się już coś pomieszało, przecież E
4 nie oznacza ilość wektrów a
ilość współrzędnych
2 lut 12:51
Hugo: jak bym czasem pisal to prosze o pomoc na egzaminie
2 lut 15:31
Eve: Hugo to nieetyczne
2 lut 15:35
Hajtowy: Czasem trzeba studentowi pomóc
2 lut 15:43
Eve:
2 lut 15:56
Eve: Hugo albo nie pisze, albo nie potrzebuje pomocy
2 lut 17:13
Eve: Hugo co z twoja algebrą?
2 lut 19:30
Eve: poszedł sie upić, tylko nie wiem czy z rozpaczy czy ze szczęścia
2 lut 20:17
Draghan: Dziś u nas w akademiku szaleją, bo inżynierki pozdawali...
Może i Hugo jakąś dostał?
2 lut 20:35
kyrtap:
2 lut 20:37
Eve: on zdawał algebre i nie wiem czy mu dzis nie zaszkodziłam, wolałabym wiedzieć
2 lut 20:39
Draghan: Dlaczego miałabyś zaszkodzić, Eve?
2 lut 20:46
Eve: nie wiem, czy mu dobrze wszystko objaśniłam, miałam z algebra doczynienia wieki temu
2 lut 20:47
Draghan: Nie martw się.
Hugo wróci i Ci podziękuje.
Jak będzie w stanie.
2 lut 20:51
Eve: no to pewnie dopiero jutro wieczorem, bo na środe ma fizyke
2 lut 20:54
Draghan: Tak a'propos fizyki − z piątkowego koła zdało ~20 osób na naszym kierunku, licząc razem z
powtarzającymi.
2 lut 21:10
Eve: na ilu?
2 lut 21:12
Draghan: 273 osoby.
2 lut 21:15
Eve: 
matko kochana, nie mam pytań
2 lut 21:16
2 lut 21:25
Abey: Draghan, to co było na tym kole?
Masz zdjęcie może?
2 lut 21:40
2 lut 22:32
Abey: No łatwe te zadania nie były.
2 lut 22:45
Eve: a jak wczoraj?
3 lut 11:46
bezendu:
Kogo matma położyła to położyła, ale nie wszystkich !
3 lut 13:31
3 lut 13:39
52: bezendu tak trzymać, kiedy piszesz na 5.5 ?
3 lut 13:39
Eve: już czytałam, zadowolona nie jestem
3 lut 13:40
kyrtap: Eve ważne, że walczył ja tam jestem z Hugo zadowolony
3 lut 13:45
Eve: jak zda, to się pocieszę
3 lut 13:46
kyrtap: trochę utrudnioną ma matmę, ja sam bym ciekawe czy sobie poradził z każdym zadaniem i sam
pewnie bym poległ
3 lut 13:47
Eve: ja to się cieszę, że mam to juz za sobą, nie miałam pisemnych egzaminów a kolokwia były z małej
partii materiału i rzadko. Teraz miałabym chyba kłopoty żeby to pozdawać
3 lut 13:57
bezendu:
52 dziś o 16 pisałem, zrobiłem aż 3 zadania
Tylko pytanie czy dobrze
3 lut 19:01
Eve: a ile ich było ?
3 lut 19:06
Takie zadanka miały pierwszaki http://vpx.pl/i/2015/02/02/10959840_709671589148242_7312135346891662617_n.jpg
Grupa poprawiających miała inne jakieś.
