potegi
adam: mam zapisać to w jednej postaci
potęgi
0,2−13 * 257
21 sty 15:56
adam: | 1 | | 1 | | 1 | |
| −13 * |
| −14 = |
| −27  |
| 5 | | 5 | | 5 | |
21 sty 16:08
21 sty 16:09
5-latek: Moze byc tak jak zapisales
| | a | | b | |
a dalej = 527 ze wzoru |
| −x= |
| x |
| | b | | a | |
21 sty 16:11
adam: teraz mam trudniejszy przykład
√48 −√75 + √12
nie bardzo wiem jak do niego podejść
mam takie coś po rozłożeniu liczb
√4*12−√5*15+√2*6
21 sty 16:12
5-latek: a moze tak
48=16*3
75=3*25
12=3*4
i teraz √48−√75+√12= √16*3−√25*3+√4*3= moze dalej Ty
21 sty 16:16
adam: 4√3−5√3+2{3} = 4(32) − 5(32) + 2(32) = mamy inne podstawy i te same
wykladniki co dalej?
21 sty 16:20
5-latek: Tu po wyliczeniu 4√3−5√3+4√3= 3√3= 31*31/3 = policz
21 sty 16:24
adam: fakt tępy jestem

chyba winno być 4
√3 − 5
√3 + 2
√3
21 sty 16:27
adam: =√3 = 3 do potęgi 12?
21 sty 16:28
5-latek: tak masz racje √3=31/2
Robilem inne zadanie i z rozpedu napisalen 31/3
21 sty 16:32
adam: no nawet się zastanawiałem skąd się wzieło te 31/3
21 sty 16:32
5-latek: 16:27 Tak Ty masz racje
napisz ile to sie rowna i nawet nie bedzie potrzeby dalej rozpisywac
21 sty 16:34
5-latek: to 31/3 by bylo gdybysmy mieli 3√3
21 sty 16:35
adam: teraz mam innego typu zadanie
liczby są takie : a = 5−3
√3 i b=2−
√3
i mam wykonać takie działanie
a
−1
| | 1 | |
to chyba proste bo wyjdzie mi |
| i tu usuwam niewymiernosc w mianowniku, tak? |
| | 5−3√3 | |
| | 5+3√3 | |
to będzie |
| ? |
| | (5−3√3)(5+3√3) | |
21 sty 16:36
adam: 16:35 aha, dobrze, że napisałeś
to wynik z 16:27 będzie 3(12)
21 sty 16:37
5-latek: tak tylko dalej napisz ile to sie rowna
21 sty 16:38
adam: | | 5+3√3 | |
do 16:36, przy czym używam wzoru skr. mnożenia i będzie to |
| |
| | 25−27 | |
21 sty 16:38
adam: | | 1 | |
5−latek mówisz o tym przykładzie 16:27? to napisałem, że równa się 3 do potęgi |
| , źle  |
| | 2 | |
a teraz rozwiązuje przyklad z 16:36
21 sty 16:39
5-latek: Post 16:37 zostaw to w postaci √3
21 sty 16:40
adam: ale to muszę napisać w postaci potęgi
21 sty 16:43
5-latek: Zaraz zebysmy sie tu nie poplatali . Ten przyklad gdzie jest to
√3 co wyjdzie masz tez
zapisac w postaci potegi ?
Jesli tak to zapisz 3
1/2 jesli nie to zostaw normalnie
√3
21 sty 16:43
adam: ok kontynuując to z 16:36 to
| 5+3√3 | |
| = i tak zostawić? |
| −2 | |
21 sty 16:44
adam: 5−latek tak, trochę to poplatałem może zbyt duzo postów naraz , teraz jest ok, wynik do tamtego
21 sty 16:45
5-latek: 16:44 tak zostaw bo z tym juz nic nie zrobisz
Ale tam widzialem jeszce bylo b) a co masz zrobic z b?
21 sty 16:49
adam: b) √b2−√a2 =
czyli = √(2−√3)3 − √(5−√3)3
czyli tak ((2−√3)3)(12) − ((5−√3)3)(12)
21 sty 16:54
adam: źle......
powinno być
((2−
√3)
2)
(12) − ((5−
√3)
2)
(12)
i potęgi mnoże i wychodz 1, czyli pozbywam się kwadratu i pierwiastka

21 sty 16:56
adam: kończąc 2−√3 − 5 +3√3 = −3 − 2√3
21 sty 16:58
5-latek: Zaraz . Chwilka to nie tak
mamy tak a= 5−3√3 i b= 2−√3 i masz wykonac takie edzialanie
√b2−√a2 tak? czy sa inne dane najpierw odpowiedz na to pytanie
21 sty 17:02
adam: nie ma, jest tylko a i b , które podałeś i należy wykonać działanie − dokładnie tak jak
napisałes
21 sty 17:03
adam: czy tak? −3 − 2√3
21 sty 17:11
5-latek: czyli mamy tak √(2−√3)2−√5−3√3)2
Nie robisz tak jak w poscie 16:54 i 16:56
Korzystamy z tego ze √x2=|x| i np √(2−√3)2= |2−√3| ale √3=1,73 wiec 2−1,73>0
czyli to co w module >0 wie opuszcajac wartosc bezwzgledna nie zmieniamy znaku wiec
|2−√3|=2−√3
√5−3√3)2= |5−3√3| liczymy tak samo jak poprzednio 3√3= 3*1,73>5 czyli to co w
module 5−3√3<0 czyli opuszczajac wartosc bezwzgledna zmieniamy znak na przeciwny (to
wszysko wynika z definicji wartosci bezawzglednej zobacz i przypomnij sobie )
wiec |5−3√3|=−(5−3√3)=−5+3√3= 3√3−5
Teraz nasze cale dzialanie mozemy zapisac tak
= |2−√3|−|5−3√3|= 2−√3−(3√3−5)= licz dalej
21 sty 17:18
adam: aaa już rozumiem, dzięki za dokładny komentarz do działań,
to będzie tak: 2−√3−3√3+5 = 7−4√3
21 sty 17:21
adam: mam kolejne bardzo trudne zadanie;
są takie zbiory B = (−
∞,2> i C=<−1,3)
trzeba wykonac dzialania:
a)B\C
jak to zrobić


21 sty 17:26
5-latek: Tak by wychodzilo .
A dlaczego liczyles a−1?
21 sty 17:26
adam: 5−latek, bo są 2 podpunkty w zadaniu , pierwszy policzyć a−1
i drugi √b2−√a2, chyba, że masz na myśli to, że znów się gdzieś pomyłiłem przy liczeniu
a−1
21 sty 17:27
5-latek:
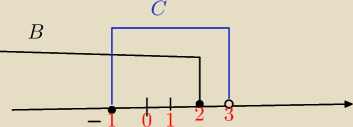
Najpierw co to oznacza
B\C jest to roznica zbiorow i oznacza tyle co nalezy do B i nie nalezy do C
Teraz odczytaj B\C jaki to bedzie przedzial
21 sty 17:33
5-latek: Nie dobrze juz rozumiem bo nie napisales dokladnie polecenia . Dlatego pytalem
21 sty 17:34
21 sty 17:36
adam: aha, już coś powoli chyba zaczynam rozumieć, czyli to będzie przedział <−1,2>
21 sty 17:37
adam: ?
21 sty 17:45
adam: a niehh, pomyliłem się, powinno być od (−∞,−1)
21 sty 17:47
5-latek: To nie bedzie ten przedzial
Popatrz jeszcze raz na rysunek . To co napisales ten przedzial nalezy do C a wedlug tego ze
nalezy do B i nie nalezy do C
Bedziemy rozpatrywali przedzial (−oo −1 tylko czy on bedzie domkniety czy otwarty ?
Teraz zobacz −1 nalezy do B a takze nalezy do C a ma nie nalezec do C wiec to bedzie
przedzial otwarty
Zapiszmy to B\C=(−oo.−1)
Pop prostu nalezy zrobic troche przykladow i zalapiesz . Link masz
21 sty 17:47
5-latek: Ma tylko nalezec do B .

21 sty 17:48
adam: no w końcu coś zaczynam rozumieć, przejrzałem te przykłady w linku i skorygowałem wynik
teraz mam taki przykład b)B ∩ C = to będzie = <−1,2>?
21 sty 17:53
5-latek: A napisz tutaj sume iloczyn i roznice C\B
21 sty 17:53
5-latek: Iloczyn Bi C dobrze
21 sty 17:55
adam: suma B∪C = (−∞,−3)
21 sty 17:55
adam: różnica C\B=(2,3)?
21 sty 17:56
adam: tam do sumy to miało być (−∞,3)
21 sty 17:56
5-latek: Roznica i suma OK

21 sty 17:59
adam: następne trudne zadanie
Przybliżenie z nadmiarem liczby dodatniej x wynosi 13. Błąd względny tego przybliżenia wynosi
0,04. oblicz x.
jak do tego zadania się wziąć?
21 sty 18:08
21 sty 18:11
adam: ok, w każdym bądź razie spróbuje zrobić i tutaj napisze
21 sty 18:12
adam: ok, rozpisałem to tak:
x≈13
x≈a
Bw = 0,04
x=?
tak to rozumie, ale chyba się myle, ponadto nie bardzo wiem jak tutaj wyjsc z wart. bezwględnej
21 sty 18:20
adam: 5−latek
w takim razie zostawię te zadanie na krótkie później,
mam tutaj następne trudne zadanie
Podaj zbiór liczb który spełnia jednoczesnie nierownosc |x|<3 i |x|≥2.
nie bardzo wiem, jak się do tego zabrać
21 sty 18:23
5-latek: Musisz nauczyc sie rozwiazywac takie proste nierownosci z wartoscia bezwzgledna
|x|<a wtedy x<a i x>−a popatrz na spojnik czyli i wiec musisz
wyznaczyc czesc wspolna rozwiazan
Na razie rozwaiz to rownanie |x|<3 i wyznacz czesc wspolna
21 sty 18:29
5-latek: nalepiej na osi liczbowe bo wtedy bedziesz lepiej widzial
21 sty 18:30
5-latek: NO co tam tak dlugo ?
21 sty 18:36
adam: ok, generalnie chodzi mi o taką kwestie
|x|=a⇔(x=a∨x=−a).
to tutaj |x|<3
czyli x<3 lub x>−3 tak? bo przy minusie odwracamy znak?
21 sty 18:36
adam: 5−latek zastanawiałem się
21 sty 18:36
5-latek: Napisalem jaki spojnik ma byc jesli mamy nierownosc |x|<a
21 sty 18:38
adam:
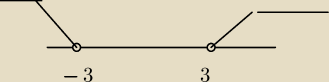
?/
21 sty 18:39
5-latek: Na razie to rozwiazemy to zadanie a potem CI cos pokaze
21 sty 18:40
adam: źlee
21 sty 18:40
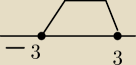
adam:
21 sty 18:41
adam: czyli x należy (−3,3)?
21 sty 18:42
5-latek:
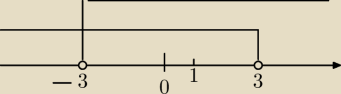
18:39 co to jest ? zle to jest zrobione
Teraz wyznacz czesc wspolna tych rozwiazan
21 sty 18:43
adam: reasumując
|x|<a
x<3 i x>−3
x∊(−3,3)
21 sty 18:43
5-latek: czyli x nalezy (−3,3)
21 sty 18:44
adam: no jakoś idzie mi to,
okej, teraz musze rozważyć przypadek |x|≥2
to będzie x>2 i x<−2?
21 sty 18:45
5-latek: Terazn mamy taka nierownosc |x|≥2
taka nierownosc jest rownowazna nierownosciom x≥2 lub x≤−2
Zwroc uwage na spojnik lub to oznaavcza ze bedziesz musial wyznaczyc sume rozwiazan
Wiec rozwiaz teraz ta nierownosc
21 sty 18:47
5-latek: 18:45 zwroc uwage na zwroty nierownosci ktroa masz rozwiazac . Ty masz miec nierownosc slaba
czyli ≥ a nie ostra czyli >
21 sty 18:49
adam:
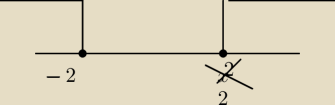
x∊(−
∞,−2> ∪ x∊<2,+
∞)?
21 sty 18:50
adam: 5−latek , aha , dobrze wiedzieć, już mi się to wszystko powoli układa w głowie
21 sty 18:50
5-latek: Jakbys mial rozwiazac taka nierownosc |x|>2 to wtedy x>2 lub x<−2
21 sty 18:51
adam: wcześniej wydawało mi się to takie trudne, teraz to zrozumiałem i jest to proste
21 sty 18:53
adam: 5−latek mam kolejne trudne zadanie
rozwiąż równanie 1−|3x−2|=3
mam wart. bezwzględną , normalnie to bym rozważył to tak:
|3x−2| >0 |3x−2|<0
3x−2 −3x+2
ale tutaj mam więcej czynników, i przeniosę tą 1 na drugą stronę, ale zostanie mi taka kwestia
do rozwiązania, a mianowicie −|3x−2| i co w takim przypadku robić?
21 sty 18:59
5-latek:

Godzina 18:50 OK.
Tylko taka mala uwaga . Rozwiazania rysujemy na osi liczbowej
A os liczbowa jet to prosta ktora ma zwrot zanaczony punkt zerowy i jednostke
Tak to powinno wygladac rozwiazanie tej nieronosci
Wiec narysuj teraz na osi liczbowej rozwiazania obu tych nieronosci i napisz przedzily gdzie
rozwiazna sie pokrywaja
21 sty 18:59
adam: 5−latek, ok już rysuje
21 sty 18:59
adam: ja myślałem, że to koniec tamtego zadania
21 sty 19:00
5-latek: Najpierw to zadanie skoncz . Potem ciekawostka i zadanie nastepne OK?
21 sty 19:02
adam:
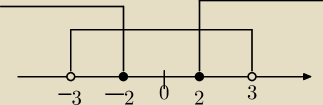
x∊(−3,−2> u <2,3)
pokrywają, to znaczy, że iloczyn

21 sty 19:03
adam: 5−latek ok
21 sty 19:03
adam: 19:03, głupote powiedziałem
21 sty 19:07
5-latek: Dobrze . Teraz taka ciekawosta .Zeby wiedziec jak mamy nierownosc kiedy dac spojnik albo lub
to zobacz Mamy taki zwrot < . Teraz obracamy go 0 90 stopni w prawo i dostamniemy ⋀ a to
jest spojnik i z logiki (czyli liczymy iloczyn (czesc wspolna rozwiazan . Teraz mamy
taki zwort nierownisci > obracamy goo 90 stopni i dostaniemy ⋁ czyli z logiki spojnik
lub czyli may wyznaczyc sume rozwiazn .
Napisz teraz jakie to bylo rownanie
21 sty 19:10
adam: 5−latek, fajne tego nie wiedziałem
1−|3x−2|=3
21 sty 19:11
5-latek: 19:03 −czesc wspolna rozwiazan (czyli dobrze powiedziales
21 sty 19:12
adam:

tak sobie to zobrazowałem i później sumowałem to
21 sty 19:13
adam: ok, to zacznijmy ten przykład 1−|3x−2|=3
21 sty 19:13
adam: nie bardzo wiem jak rozważyć o to −|wart bezw| ,zawartości chyba nie można pomnożyć przez −1
21 sty 19:17
5-latek: Mamy tak
1−|3x−2|=3 To jest rownanie a nie nierownosc wiec rozwiazujemy go tak wedlug tego schematu
|x|=a to x=a lub x=−a
1−|3x−2|=3
−|3x−2|=3−1(zawsze wartosc bezwzgledna zostawiamy po lewo a wiadome przenosimy na prawo
−|3x−2|=2 (teraz pomnozymy obie strony rownania przez (−1) zeby sie pozbyc minusa przed
wartoscia bezwzgledna wiec dostaniemy
|3x−2|=−2 (teraz zastanow sie dobrze i powiedz czy to rownanie ma rozwiaznia czy nie ma
rozwiazan
jesli nie ma to dlaczego ?
21 sty 19:20
5-latek: Tu sie przyda znajomosc definicji wartosci bezwzglednej
21 sty 19:21
adam: nie ma liczby której wartość bezwzględna jest równa −2?
21 sty 19:24
adam: bo |x|= a
a
a to ≥0?
21 sty 19:25
5-latek: Powiem Ci

czyli co napiszsez w rozwiazaniu ?
21 sty 19:25
adam: x∊ ∅?
21 sty 19:26
5-latek: Lepiej napisz tak . To rownanie nie ma rozwiazn .
21 sty 19:27
adam: okej, a moglibyśmy teraz rozważyć taki przypadek, równanie |3x−2|=2
czyli tak: 3x−2=2 lub 3x−2=−2
3x = 4 lub 3x=0
| | 3 | |
x= |
| tak  |
| | 4 | |
21 sty 19:30
adam: i jeszcze x=0
21 sty 19:32
21 sty 19:33
5-latek: Zgubiles jedno rozwiazanie x=0 bo zobacz jak wstawimy zax=0 do rownania to |3*0−2|=2 to
|−2|=2 a to przeciez jest prawda tak ?
21 sty 19:34
adam: tak, prawda
21 sty 19:35
5-latek: 
21 sty 19:37
adam:
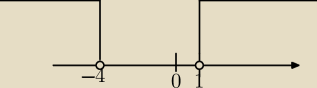
ok, to tutaj mam nierówność, bazując na tym co się dowiedziałem
|2x+3|>5 to:
2x+3>5 i 2x+3<−5
2x>2 i 2x<−8
x>1 i x<−4
x∊(−
∞,−4) ∪ (1,+
∞)
21 sty 19:39
5-latek: Spojnik lub nie i (jak chceszz tego wyznaczyc czesc wspolna ?
21 sty 19:43
adam: teraz mam takie zadanie:
zapisz w postaci
jednej potegi
| | 1 | |
√2 * 84 * 2−2 = 2( |
| ) * 212 * 2−2 = 26 *2−2 = 24 |
| | 2 | |
21 sty 19:43
adam: 5−latek , fakt , poomyliło mi się, ponieważ > w prawo o 90 stopni to wygląda jak lvb,
myślałem żeby napisać lub, a wyszło mi i, eh
czyli mówisz, że jeśli mamy tylko jedną nierówność to nie wyznaczamy części wspólnej, bo fakt
jej nie ma , to rozwiązaniem tylko jest x>1 i x<−4
21 sty 19:45
adam: x>1 LUB x<−4 i tak napisać odpwiedź i będzie dobrze?
21 sty 19:45
5-latek: Rozwiazanie masz napisac tak x∊(−oo,−4)U(1,oo)
| | 1 | | 1 | | 25 | | −4 | |
19:43 zle (wykladniki dodajemy |
| +12=12 |
| +(−2) czyli |
| + |
| = policz |
| | 2 | | 2 | | 2 | | 2 | |
21 sty 19:51
adam:
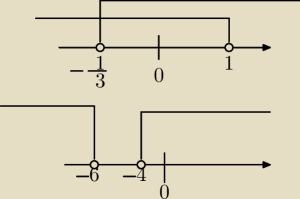
no to dobra, za kare rozwiąże sam 2 nierówności i to poprawnie
|3x−1| < 2
3x − 1 < 2 i 3x−1 > −2
3x <3 i 3x > −1
|x+5| >1
x+5> 1 lub x+5<−1
x>−4 lub x<−6
21 sty 19:51
adam: przy czym do |3x−1| < 2
|x+5| >1
x∊(−
∞,−6) ∪ (−4,+
∞)
21 sty 19:54
5-latek: Zawsze pisz rozwiazania bo nauczyciel nie musi sie domylac .
| | 1 | |
np 1 nierownosc x nalezy (− |
| ,1) |
| | 3 | |
druga napisz sam
21 sty 19:55
adam: | | 1 | | 1 | | 21 | |
poprawka do √2 * 84 * 2−2 = 2( |
| ) * 212 * 2−2 = 210 |
| = 2( |
| ) i tak |
| | 2 | | 2 | | 2 | |
zostawić?
21 sty 19:57
5-latek: Znowu zle popraw zapis = 210+1/2=221/2
21 sty 20:03
adam: 221/2 , tak samo mi wyszło, przy poście 19:57 miałem na myśli potęgę ale jakoś mi nie
wyszła (użyłem złego kodu)
21 sty 20:08
5-latek: No dobrze
21 sty 20:10
adam: mam kolejny przykład
| | 81 | | 34 | | 34 | |
( |
| )2 = ( |
| )2= ( |
| )2 = |
| | 3−4 * √27 | | 3−4+3/2 | | 3−5/2 | |
| | 34 | |
( |
| )2 = (34* 35/2)2 = (313/2)2 = 313 , tak? |
| | | |
21 sty 20:16
5-latek: Jestem juz zmeczony ale sprobuje CI pomoc w tym przykladzie (prace klasowa piszsesz ?
Zatrzymajmy sie po drugim znaku = wiec mamy tak
| | 34 | |
( |
| )2 = to sie robi tak Podnosisz licznik do 2 i mianownik do 2 zgodnie z |
| | 3−5/2 | |
zasada sztuki
| | (34)2 | | 38 | |
Wiec mamy |
| = |
| |
| | ( 3−5/2)2 | | 3−25/4 | |
teraz mamy jednakowe podsatwy wiec mozemy wykladniki odjac =3
8−(−25/4 i terz policz
popatrz na przeostani wzor od dolu co do podnoszsenia do potegi
https://matematykaszkolna.pl/strona/186.html
21 sty 20:31
5-latek: i w tym samym linku tez wzor 6 od dolu
21 sty 20:32
adam: ja też już jestem zmęczony, dzięki za pomoc dużo się nauczyłem, po prostu zdałem sobie
sprawę,że już czas wziąć się za matme i chciałem co nieco sie nauczyc−przypomnieć, dużo mi
pomogłeś
21 sty 20:34
5-latek: 
21 sty 20:35

 chyba winno być 4√3 − 5√3 + 2√3
chyba winno być 4√3 − 5√3 + 2√3




 Najpierw co to oznacza
B\C jest to roznica zbiorow i oznacza tyle co nalezy do B i nie nalezy do C
Teraz odczytaj B\C jaki to bedzie przedzial
Najpierw co to oznacza
B\C jest to roznica zbiorow i oznacza tyle co nalezy do B i nie nalezy do C
Teraz odczytaj B\C jaki to bedzie przedzial


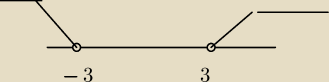 ?/
?/

 18:39 co to jest ? zle to jest zrobione
Teraz wyznacz czesc wspolna tych rozwiazan
18:39 co to jest ? zle to jest zrobione
Teraz wyznacz czesc wspolna tych rozwiazan
 x∊(−∞,−2> ∪ x∊<2,+∞)?
x∊(−∞,−2> ∪ x∊<2,+∞)?
 Godzina 18:50 OK.
Tylko taka mala uwaga . Rozwiazania rysujemy na osi liczbowej
A os liczbowa jet to prosta ktora ma zwrot zanaczony punkt zerowy i jednostke
Tak to powinno wygladac rozwiazanie tej nieronosci
Wiec narysuj teraz na osi liczbowej rozwiazania obu tych nieronosci i napisz przedzily gdzie
rozwiazna sie pokrywaja
Godzina 18:50 OK.
Tylko taka mala uwaga . Rozwiazania rysujemy na osi liczbowej
A os liczbowa jet to prosta ktora ma zwrot zanaczony punkt zerowy i jednostke
Tak to powinno wygladac rozwiazanie tej nieronosci
Wiec narysuj teraz na osi liczbowej rozwiazania obu tych nieronosci i napisz przedzily gdzie
rozwiazna sie pokrywaja
 x∊(−3,−2> u <2,3)
pokrywają, to znaczy, że iloczyn
x∊(−3,−2> u <2,3)
pokrywają, to znaczy, że iloczyn
 tak sobie to zobrazowałem i później sumowałem to
tak sobie to zobrazowałem i później sumowałem to
 czyli co napiszsez w rozwiazaniu ?
czyli co napiszsez w rozwiazaniu ?


 ok, to tutaj mam nierówność, bazując na tym co się dowiedziałem
|2x+3|>5 to:
2x+3>5 i 2x+3<−5
2x>2 i 2x<−8
x>1 i x<−4
x∊(−∞,−4) ∪ (1,+∞)
ok, to tutaj mam nierówność, bazując na tym co się dowiedziałem
|2x+3|>5 to:
2x+3>5 i 2x+3<−5
2x>2 i 2x<−8
x>1 i x<−4
x∊(−∞,−4) ∪ (1,+∞)
 no to dobra, za kare rozwiąże sam 2 nierówności i to poprawnie
|3x−1| < 2
3x − 1 < 2 i 3x−1 > −2
3x <3 i 3x > −1
no to dobra, za kare rozwiąże sam 2 nierówności i to poprawnie
|3x−1| < 2
3x − 1 < 2 i 3x−1 > −2
3x <3 i 3x > −1
