Wykazywanie.
Blue: zad. 11 Udowodnij, że prosta y= 3x−16 jest styczna do wykresu funkcji f(x) = x
3−9x.
http://i59.tinypic.com/2em1oy1.jpg
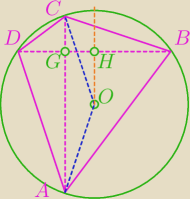
zad.12 W czworokącie ABCD przekątne są prostopadłe oraz na tym czworokącie można opisać
okrąg o środku O. Udowodnij, że łamana AOC dzieli czworokąt ABCD na dwie figury o równych
polach.
http://i62.tinypic.com/22ywdv.jpg
Może mi ktoś powiedzieć, czy dobrze zrobiłam te zadania
15 sty 18:35
Mila:
W (11) trochę więcej wyjasnien.
f'(x0)=3
Moze być.
15 sty 22:01
Blue: 12 może być?
15 sty 22:04
Mila:
Zadanie 2 jutro. Rozważyłaś tylko szczególny przypadek, gdy środek okręgu opsanego na
czworokacie leży na przekątnej.
15 sty 22:34
Kacper:
16 sty 10:11
Tadeusz:
... CHYBA WSZYSTKO WIDAĆ −
16 sty 10:36
Blue: Aha, czyli 11 może być a 12 źle... Tadeusz, możesz to objaśnić?
16 sty 14:09
Tadeusz:
AC oznaczy jako p zać BD jako q
Pole czworokąta jest sumą pól trójkątów ACD i ABC
| | |AC|*|DG|+|AC|*|BG| | | |AC|(|DG|+|BG|) | | pq | |
czyli S▱ABCD= |
| = |
| = |
| |
| | 2 | | 2 | | 2 | |
Zauważ, że S
▱AOCD=S
ΔACD+S
ΔAOC (suma wysokości tych trójkątów to q/2)
16 sty 14:29
Blue: | | pq | |
Czyli wystarczy , że jeszcze zapiszę, że pole AOCD = |
| i już mam wykazane , tak? |
| | 4 | |
16 sty 14:51
Blue: Myślę, że największym problemem było zauważenie tutaj tego, że suma tych wysokości wynosi
q/2...
16 sty 14:52
Tadeusz:
aż tak trudne to nie jest −
16 sty 15:02
16 sty 15:05
Blue: Niby nie ale wiesz − z planimetrii wszystko jest trudne dopóki się tego nie zauważy, jak już
się zauważy , to jest proste
Dzięki za pomoc
16 sty 15:10
Mila:
To po problemie. Mój pomysł na 12 zadanie taki, jak Tadusza. Pozdrawiam.
16 sty 17:03
16 sty 18:08
