 Witam . mam jesszce takie pytanie co do przeciwobrazu f−1
Chcialbym to naprawde dobrze zrozumiec
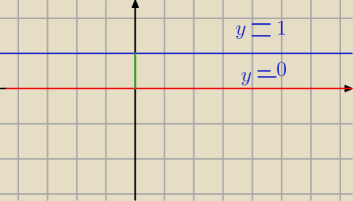
mamy funkcje stala y=b niech b=1 lub b=0 . mamy znalezc przeciobraz na przedziale (0,1)
Na zielono oznaczylem ten przedzial
Skoro 0 i 1 nie nalezy do przedzialu to oznacza wedlug mnie ze te funkcje nie osiagna swoich
wartosci wiec nie znajdziemy takich argumentow (xow dla ktorych watosc funkcji y=0 wynosi 0
i y=1 wynosi 1
czyli przeciobrazem dla tych funkcji w tym przedziale bedzie zbior pusty .
Inaczej by sie przedstawiala sprawa gdyby byl to przedzial <0,1> wtedy zarowno dla y=0 i
y=1 przeciwobrazem bedzie zbior liczb R gdzyz dla wszystkich xow wartosc y=0 wwynosi 0 i
y=1 wynosi 1 .
Witam . mam jesszce takie pytanie co do przeciwobrazu f−1
Chcialbym to naprawde dobrze zrozumiec
mamy funkcje stala y=b niech b=1 lub b=0 . mamy znalezc przeciobraz na przedziale (0,1)
Na zielono oznaczylem ten przedzial
Skoro 0 i 1 nie nalezy do przedzialu to oznacza wedlug mnie ze te funkcje nie osiagna swoich
wartosci wiec nie znajdziemy takich argumentow (xow dla ktorych watosc funkcji y=0 wynosi 0
i y=1 wynosi 1
czyli przeciobrazem dla tych funkcji w tym przedziale bedzie zbior pusty .
Inaczej by sie przedstawiala sprawa gdyby byl to przedzial <0,1> wtedy zarowno dla y=0 i
y=1 przeciwobrazem bedzie zbior liczb R gdzyz dla wszystkich xow wartosc y=0 wwynosi 0 i
y=1 wynosi 1 .
| x | ||
I jeszce jedno . Jesli mam y= | dla xnie rowna sie 0 to moja funkcja bedzie wygladala tak | |
| x |
 więc
f−1=R\{0} na twoim przedziale
więc
f−1=R\{0} na twoim przedziale

 ZA jakis czas nastepne zadanka . Najgorszse sa te gdzie sa przedzialy i trzeba znalezc funkcje
ZA jakis czas nastepne zadanka . Najgorszse sa te gdzie sa przedzialy i trzeba znalezc funkcje



 Niedawno wstalem bo do pozna czytalem jeszcze o tych funkcjach
Niedawno wstalem bo do pozna czytalem jeszcze o tych funkcjach