pochodne
kyrtap: Mam znaleźć wszystkie ekstrema lokalne funkcji:
f(x) = |x
2−5x−6|
| | ⎧ | x2−5x−6 dla x2−5x−6>0 | |
| f(x) = | ⎨ | |
|
| | ⎩ | −(x2−5x−6) dla x2−5x−6<0 | |
| | ⎧ | x2−5x−6 dla x∊(−∞,−1> ∪ <6,∞) | |
| f(x) = | ⎨ | |
|
| | ⎩ | −x2 +5x +6 dla x∊(−1,6) | |
| | ⎧ | 2x−5 dla x∊(−∞,−1> ∪ <6,∞) | |
| f'(x) = | ⎨ | |
|
| | ⎩ | −2x+5 dla x∊(−1,6) | |
| | 1 | | 1 | |
f'(x) = 0 ⇔ 2x − 5 =0 ⇔ 2x = 5 /:5 ⇔ (x = 2 |
| ⋀ x∊D) ⇒ x=2 |
| |
| | 2 | | 2 | |
| | ⎧ | 2 dla x∊(−∞,−1> ∪ <6,∞) | |
| f''(x) = | ⎨ | |
|
| | ⎩ | −2 dla x∊(−1,6) | |
jak sprawdzić teraz czy są te ekstrema

6 sty 21:52
kyrtap: 
6 sty 22:03
Tadeusz:
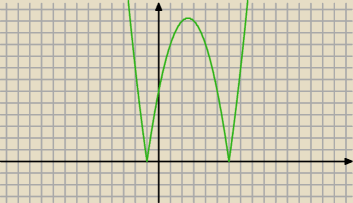
6 sty 22:04
kyrtap: Tadku a jak bez wykresu do tego dojść?
6 sty 22:05
kyrtap: 
6 sty 22:12
Tadeusz:
W przedziale <−1,6>
f(x)=−x2+5x+6
f'(x)=−2x+5
f'(x)=0 2x=5 x=2,5 mieści się w przedziale
przy przejściu przez punkt x=2,5 pochodna zmienia znak z + na − czyli max
6 sty 22:18
Tadeusz:
albo tak jak zrobiłeś ... drugą pochodną
6 sty 22:19
kyrtap: no dobra wyliczyłem drugą pochodną
| | 1 | |
i teraz f''(2 |
| ) = −2 <0 czyli maksimum lokalne właściwe tak  |
| | 2 | |
6 sty 22:22
Tadeusz:
dokładnie
6 sty 22:26
kyrtap: dzięki wielkie Tadku

6 sty 22:27
john2: A czy jeszcze czasem funkcja ta nie ma minimów w x = −1 i x = 6 ?
Na podobnej zasadzie co funkcja f(x) = |x| ma minimum w x = 0.
6 sty 22:39
john2: Ktoś może potwierdzić?
7 sty 13:04
J:
..oczywiście,że ma ...
7 sty 13:09
kyrtap: ma

7 sty 13:11
J:
popatrz na wykres ... nie ma ..?
7 sty 13:16
john2: Poza tym pierwsza pochodna zmienia znak w tych punktach.
w x = −1
z 2x − 5 na −(2x − 5) czyli −2x + 5
w x = 6
z −(2x − 5) na 2x − 5
7 sty 13:20
kyrtap: czyli są jeszcze dwa minima lokalne właściwe?
7 sty 13:21
kyrtap: a jak to obliczeniowo zapisać? bo gdy liczyłem f'(x) = 0 wyszło mi tylko jedno ekstremum
7 sty 13:22
J:
.. w tych punktach funkcja nie jest różniczkowalna ( nie ma pochodnej ) ...
7 sty 13:22
kyrtap: czyli jak to zapisać że są dwa minima?
7 sty 13:23
J:
zauważ,ze jezeli funkcja f(x) ma miejsce zerowe, to funcja If(x)I musi mieć minimum lokalne ..
( przecież odbijasz to, co jest pod osią OX)
7 sty 13:28
kyrtap: czyli mam policzyć miejsca zerowe dla x2 −5x − 6?
7 sty 13:29
J:
..tak ..
7 sty 13:32
kyrtap: J tak na dobrą sprawę to jest szczególny przypadek znajdywania ekstremów jeśli chodzi o funkcję
z wartością bezwzględną prawda?
7 sty 13:34
J:
patrz wpis 13:28
7 sty 13:41
kyrtap: ok wbiję to sobie do główki bardzo dziękuje

7 sty 13:42
7 sty 13:46
john2: Hmm. Teraz znalazłem taki wątek i patrząc na ostatni post Bogdana:
https://matematykaszkolna.pl/forum/153710.html
się zastanawiam, czy to badanie ciągłości, o którym mówi Gray, przesądza sprawę, skoro
funkcji w ekstremum nie musi być ciągła.
7 sty 14:01
Gray: Wtrącę się: przesądza

Chodzi o to, że jeżeli pochodna w punkcie zmienia znak (tzn. na lewo
od punktu jest np. dodatnia, na prawo ujemna, w samym punkcie pochodnej może nie być), to
funkcja
nie musi mieć w tym punkcie ekstremum. Jeżeli jest ciągła, ekstremum będzie. Tak
było w tym przytoczonym poście.
7 sty 19:02
Gray: Może inaczej: z faktu, że jest nieciągła, nie wynika, że nie ma ekstremum. Ogólnie, dla funkcji
nieciągłych są najciekawsze przypadki: pochodna może zmieniać znak w punkcie nieciągłości a
ekstremum może nie być, lub też (co ciekawsze) pochodna może nie zmieniać znaku, a ekstremum
może być.
7 sty 19:05
john2: Już miałem Cię szukać, Gray.
Rozumiem. Faktycznie. Jeśli jest ciągła, potwierdza to, że jest tam ekstremum.
Tylko gdyby wyszło, że funkcja nie jest w tym punkcie ciągła, czy moglibyśmy powiedzieć, że
ekstremum nie ma w tym punkcie? Bo widać ku mojemu zdziwieniu (choć to wcale dziwne może nie
jest) na rysunku Bogdana, że funkcja może mieć ekstremum tam, gdzie nie jest ciągła.
7 sty 19:10
john2: Aha, ciekawe. Byłbyś może w stanie polecić jakiś podręcznik, gdzie jest ten temat gruntownie
poruszony? Bo ja na na razie uczę się, zbierając strzępy informacji na ten temat z internetu i
gubię się
7 sty 19:13
kyrtap: podpinam się pod post johna

7 sty 20:30
Gray: Niestety, nie znam żadnego podręcznika, który omawiałaby kwestię ekstremów funkcji nieciągłych
i (lub) nieróżniczkowalnych. Pewnie dlatego, że nie ma żadnych ogólnych narzędzi.
Jak już pisałem, dla funkcji nieciągłej w punkcie, badanie czy jest ekstremum, czy nie
sprowadza się do definicji. Jakiekolwiek zachowanie się pochodnej w sąsiedztwie punktu nie
mówi nic o ekstremum. Ani warunków koniecznych, ani wystarczających nie ma.
7 sty 20:47
kyrtap: Gray a polecisz książkę która zwięźle omawia teorię zarówno ze szkoły średniej jaki i na
studiach

7 sty 20:50
Gray: Nic nowego nie napiszę. Z czystym sumieniem każdemu mogę polecić serię Gewerta, Skoczylas i
spółki:
http://www.gis.wroc.pl/books.htm
Świetnie napisane prawie 30 tomów z różnych działów matematyki, masa przykładów,
teoria + zadania (proste i bardziej ambitne). Dla wszystkich. Kiedyś standardem był Krysicki,
Włodarski i Stankiewicz. Jak pojawiła się ta seria, wszystko się zmieniło

Żeby było jasne,
nie jestem z nimi związany w żaden sposób, nie płacą mi za reklamę, nie mieszkam i nie
studiuję we Wrocławiu

Odwalili kawał dobrej roboty i za to im brawo.
Jeżeli chodzi o studentów matematyki i analizę, każdy powinien mieć Fichtenholza.
http://ksiegarnia.pwn.pl/autor/Grigorij+M.+Fichtenholz.html
Ułatwia
życie.
Z nowości, ostatnio pojawiły się genialne zbiory zadań z analizy (dla matematyki, ale nie
tylko):
http://ksiegarnia.pwn.pl/produkt/4560/zadania-z-analizy-matematycznej-cz-1.html
Zadania z rozwiązaniami. Dobra rzecz. Chyba tyle.
8 sty 08:30
john2: Dzięki Gray.
8 sty 10:57
kyrtap: 
8 sty 13:36








 Chodzi o to, że jeżeli pochodna w punkcie zmienia znak (tzn. na lewo
od punktu jest np. dodatnia, na prawo ujemna, w samym punkcie pochodnej może nie być), to
funkcja nie musi mieć w tym punkcie ekstremum. Jeżeli jest ciągła, ekstremum będzie. Tak
było w tym przytoczonym poście.
Chodzi o to, że jeżeli pochodna w punkcie zmienia znak (tzn. na lewo
od punktu jest np. dodatnia, na prawo ujemna, w samym punkcie pochodnej może nie być), to
funkcja nie musi mieć w tym punkcie ekstremum. Jeżeli jest ciągła, ekstremum będzie. Tak
było w tym przytoczonym poście.


 Żeby było jasne,
nie jestem z nimi związany w żaden sposób, nie płacą mi za reklamę, nie mieszkam i nie
studiuję we Wrocławiu
Żeby było jasne,
nie jestem z nimi związany w żaden sposób, nie płacą mi za reklamę, nie mieszkam i nie
studiuję we Wrocławiu  Odwalili kawał dobrej roboty i za to im brawo.
Jeżeli chodzi o studentów matematyki i analizę, każdy powinien mieć Fichtenholza. http://ksiegarnia.pwn.pl/autor/Grigorij+M.+Fichtenholz.html
Ułatwia
życie.
Z nowości, ostatnio pojawiły się genialne zbiory zadań z analizy (dla matematyki, ale nie
tylko): http://ksiegarnia.pwn.pl/produkt/4560/zadania-z-analizy-matematycznej-cz-1.html
Zadania z rozwiązaniami. Dobra rzecz. Chyba tyle.
Odwalili kawał dobrej roboty i za to im brawo.
Jeżeli chodzi o studentów matematyki i analizę, każdy powinien mieć Fichtenholza. http://ksiegarnia.pwn.pl/autor/Grigorij+M.+Fichtenholz.html
Ułatwia
życie.
Z nowości, ostatnio pojawiły się genialne zbiory zadań z analizy (dla matematyki, ale nie
tylko): http://ksiegarnia.pwn.pl/produkt/4560/zadania-z-analizy-matematycznej-cz-1.html
Zadania z rozwiązaniami. Dobra rzecz. Chyba tyle.
