Ekstremum funkcji.
Fizyk: Czy ta funkcja posiada ekstremum?
f(x)=3−3√x2
1 sty 12:36
john2: nie
1 sty 12:47
Blue: | | 2 | |
Nie, bo pochodna będzie wyglądać tak o ile się nie mylę : f'(x) = − |
| |
| | 33√x | |
1 sty 12:50
Fizyk: ok a co z punktem x = 0 który nie należy do dziedziny pochodnej?
1 sty 12:57
Gray: Czyli f'(x)>0 dla x<0; f'(x)<0 dla x>0. Wygląda więc na to, że ma ekstremum w x0=0; jest to
maksimum.
Nierówność 3−3√x2=3−(3√x)2≤3, prawdziwa dla x∊R, nie pozostawia wątpliwości.
1 sty 12:59
Fizyk: Wiem oczywiście o warunku konicznym istnienia ekstremum , ale pytam dlatego że kiedyś w książce
widziałem taki dziwny przykład że ekstremum było w punkcie w którym pochodna się nie zerowała
ale tez ten punkt nie należał do dziedziny pochodnej jednak należał do dziedziny funkcji
1 sty 13:00
Fizyk: Więc jak sprawdzić czy w x = 0 jest ekstremum czy nie?
1 sty 13:02
Gray: A jaki jest, w przypadku ogólnym, warunek konieczny istnienia ekstremum? Na dobrą sprawę nie ma
ani koniecznego, ani wystarczającego. Poza definicją oczywiście.
1 sty 13:03
Gray: Napisałem uzasadnienie o 12:59.
1 sty 13:03
Fizyk: Ok dzięki Gray. Czyli chodzi o to że warunek konieczny istnienia ekstremum nie jest spełniony
ale ekstremum i tak istnieje bo jest spełniony warunek wystarczający? Trochę to dla mnie nie
zrozumiale.
1 sty 13:12
Gray: Nie. Te wszystkie warunki o zerowaniu się lub zmianie znaku pochodnej działają tylko w
przypadku funkcji różniczkowalnej na przedziale, na którym szukamy ekstremum. Tutaj
funkcja nie ma pochodnej w zerze. Warunek wystarczający (zmiana znaku pochodnej) sugeruje, że
może być ekstremum. Definicja maksimum oraz nierówność z 12:59 załatwia sprawę (można było w
tym przypadku podeprzeć się również ciągłością funkcji f).
1 sty 13:15
Fizyk: Wielkie dzięki za wyjaśnienie.
Pozdrawiam.
1 sty 13:17
john2: Aha...podobnie chyba jest z f(x) = |x|
1 sty 13:25
Gray: Ta sama sytuacja.
1 sty 13:28
john2: Jeszcze chciałem dopytać, bo chcę dobrze zrozumieć:
1) Twoja nierówność z 12:59, pokazuje, że w x = 0 funkcja osiąga również ekstremum globalne
funkcji? I to oznacza, że jest tam również ekstremum lokalne?
2) Sprawdzenie ciągłości w x = 0 miałoby wyglądać tak?
limx−>0 (3 − 3√x2) = 3 − 0 = 3
f(0) = 3 − 3√02 = 3
Jest ciągła w zerze.
1 sty 14:49
Gray: Tak. Tak. Tak (lub: jest złożeniem funkcji ciągłych).
1 sty 14:59
john2: Ok. Dzięki.
1 sty 14:59
Janek191:
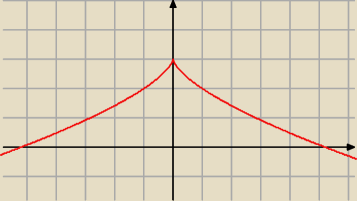
10 sie 22:28
on: Janku za gorąco ci ,ze cofnąłeś się do stycznia ?

odp. na pyt @
Fizyka Jeśli funkcja ma ostrze, to ma ekstremum ale nie ma w tym punkcie
pochodnej.
11 sie 09:34


 odp. na pyt @Fizyka Jeśli funkcja ma ostrze, to ma ekstremum ale nie ma w tym punkcie
pochodnej.
odp. na pyt @Fizyka Jeśli funkcja ma ostrze, to ma ekstremum ale nie ma w tym punkcie
pochodnej.