zadanie Blue:

	1
zad.1 Dana jest funkcja f(x) = x2−3 dla x≤2, f(x) =		x dla x>2. Zbadaj czy f jest ciągła
	2

w punkcie x₀=2 oraz czy posiada w tym punkcie pochodną. A więc ciągłość sprawdzam przez liczenie granic jednostronnych tak? Wyszło, że jest ciągła...

	1
lim		x= 1
	2

x−>2⁺ lim x²−3= 1 x−>2⁻ A jak się sprawdza czy jest pochodna?

	x2+1
zad.2 Znajdź zbiór wartości funkcji f(x) =		.
	x2+x+1

	2
Czyli liczę pochodną i wyszły ekstrema: minimum −		i maximum− 2.
	3

I teraz skąd mam wiedzieć, że nie ma nigdzie większej wartości Liczę granice w nieskończonościach, tak?

Blue: Czyli w tym 2 zadaniu granica w nieskończonościach wynosi 1 tak

Gray: Tak.

Blue:

	f(x)−f(x+h)
a z tą pochodną, to muszę obliczyć granice od tego wzoru		?
	h

Blue: O dzięki Gray, że wreszcie odpowiedziałeś^^

Blue: lim= 4−h x−>2⁻

	−1
lim =
	2

x−>2⁺ Dobrze to jest?

Eta: Można też tak:

	x2+1
y=		, x∊R
	x2+x+1

x²y+xy+y=x²+1 ⇒ (y−1)x²+yx+y−1=0

	2
Δ≥0 ⇒ y2−4(y−1)2≥0 ⇒ (y−2y−2)(y+2y+2)≥0 ⇒ ...... y∊<−2, −		>
	3

	2
ZW= <−2, −		>
	3

Blue: Eta, ale tak jak zrobiłam też może być? Dobrze są te granice od ilorazu różnicowego policzone?

Blue: aa bo Ty o innym zadanku mówisz

Blue: a no i Eta − tam nie ma minusów, to są myślniki

Eta: Achh .... źle wpisałam rozkład na czynniki ( sorry

	2
Ma być: y2−4(y−1)2≥0 ⇒(y2y−2)(y−2y+2)≥0 ⇒ (−y+2)(3y−2)≥0 ⇒y∊<		, 2>
	3

	2
ZW= <		,2>
	3

Blue: A to 1 jest dobrze?

Mila: 1) f(2)=1 i lim_x→2f(x)=1⇔f(x) jest ciągła w x=2. [np. funkcja g(x)=|x| jest ciągła dla x∊R a nie posiada pochodnej w x=0.] Musisz zbadać z definicji, czy f(x) posiada pochodną w x=2. W punktach zmiany wzoru f(x) badamy istnienie pochodnej z definicji.

Blue: Mila czyli chodzi o to, co napisałam o 16:11 i 16:04?

Mila: Masz obliczyć granicę ilorazu różnicowego:

	f(x0+h)−f(x0)
limh→0−
	h

	f(x0+h)−f(x0)
limh→0+
	h

Blue: aha, czyli wzór pomyliłam xd

Blue: https://matematykaszkolna.pl/forum/40800.html tu ktoś źle napisał

Blue:

	f(x)−f(x0)
a ja w swojej książce mam jeszcze inny zapis :
	x−x0

Blue: Mila dlaczego u Ciebie h−>0, to nie ma być tak x−>2

Mila: Tu masz teorię podaną w prosty sposób i przykłady. https://matematykaszkolna.pl/strona/357.html

Blue: Mila obliczyłam według tego, co napisałaś i wyszło : lim = 4 h−>0⁻

	1
lim =
	2

h−>0⁺ Teraz dobrze? Nie ma pochodnej, bo te granice nie są takie same

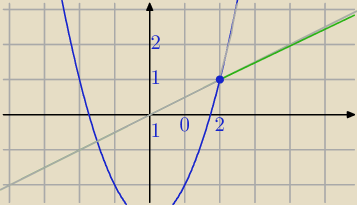
Mila: Nie ma pochodnej w x=2. Na wykresie w punkcie złączenia wykresów jest "szpic", więc nie ma pochodnej.

Blue: ok Ale takie uzasadnienie chyba nie wystarczy? Trzeba te granice obliczyć

Mila: Trzeba liczyć, lecz rysunek pomaga przewidzieć wynik. Nie zawsze wykres jest prosty, tu było łatwo narysować.