. alexis: Punkty A(−6,−1) i B(4,1) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC|==|BC|. wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka C.

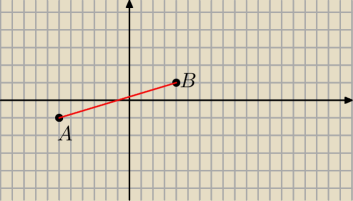
5-latek: 1. Wyznaczyc wspolrzedne srodka S odcinka AB 2. Napisac rownanie prostej prostopadlej do prostej Ab i przechodzacej przez punkt S

:): spodek wysokosci leży w połowie boku AB https://matematykaszkolna.pl/strona/1750.html

alexis: 5 latek pozniej jak mam juz punkt S (−1,0) to do rownania y=ax+b podstawiam 0=−1a+b, przekształcam na prostopadłą czyli 0=1a+b i co dalej?

5-latek: Napisz tutaj warunek na to zeby dwie proste byly prostopadle https://matematykaszkolna.pl/strona/42.html popatrz tutaj

bezendu: 1. Wyznaczasz współczynnik kierunkowy prostej ab 2. Wyznaczasz środek odcinka |AB| 3. Piszesz równanie prostej prostopadłej do prostej ab przechodzącej przez środek odcinka |AB| 4. Koniec zadania.

:): najpierw wyznacz równanie AB, potem prostopadłą do niej

bezendu: Nie rób tego co piszę : ) ! Tylko narobisz sobie pracy, wystarczy tylko współczynnik tej prostej, a nie równanie które nie jest wgl potrzebne w tym zadaniu.

5-latek: Czesc bezendu Wszystko napisales dobrze(oprocz tego ze ma wyznaczyc wspolczynnik kierunkowy prostej prostopadlej do prostej AB ) . tak wlasnie ma zrobic . Wspolrzedne srodka |AB| ma juz wyznaczone

bezendu: Ja napisałem wszystko ok, wysokość pada pod kątem prostym. Dlatego trzeba wyznaczyć współczynnik kierunkowy tej prostej i mamy tym samym już wsp prostej prostopadłej

5-latek:

	y2−y1		1−(−1)		2
wspoczynnik kierunkowy a1 prostej AB a1=		=		=		=
	x2−x1		4−(−6)		10

	1
	5

Wspolczynnik kierunkowy a₂ prostej prostopadlej do prostej AB a₁*a₂=−1(warunek

	−1
prostopadlosci prostych ) to a2=		=−5
	1/5

czyli rownanie prostej prostopadlej do AB bedzie mialo postac y=a₂+b czyli y=−5x+b Podstawiamy do tego rownania wspolrzedne punktu S (−1,0) czyli 0=−5*(−1)+b wyznacz z tego b i napisz cale rownanie tej wysokosci

alexis: dziękuje