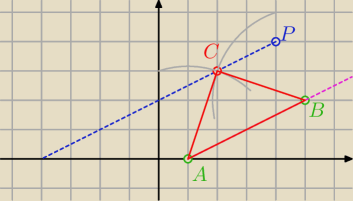
równania prostych aa: Dane są punkty A(1,0) oraz B(5,2). Na prostej k równoległej do prostej AB i przechodzącej przez punkt P(4,4) wyznacz współrzędne punktu C, który jest równo odległy od punktów A i B. Wykaż, że trójkąt ABC jest prostokątny.

daras: https://matematykaszkolna.pl/strona/1213.html https://matematykaszkolna.pl/strona/42.html

===:

===:

	2−0		1
1. Prosta przez punkty A i B ma współczynnik kierunkowy		=
	5−1		2

2. Prosta równoległa do niej i przechodząca przez P to:

	1		1
y−4=		(x−4) ⇒ y=		x+2
	2		2

3. Współrzędne punktu C to x_c, y_c C=(x_c, 0,5x_c+2) 4. Skoro jest on równoodległy od punktów A i B to: √(x_c−1)²+(0,5x_c+2−0)²=√(x_c−5)²+(0,5x_c+2−2)² ... ładnie się upraszcza i otrzymujemy x_c=2 Zatem y_c=1+2=3 C=(2,3) 5. Sprawdzamy współczynniki prostych przez punkty:

	3−0
a) A i C a1=		=3
	2−1

	3−2		1
b) B i C a2=		=−
	2−5		3

... i widać, że są to współczynniki prostych prostopadłych