zespolone
Paulina:
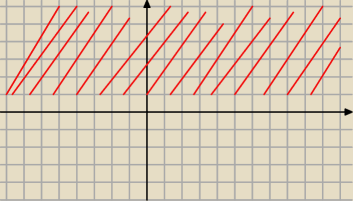
Płaszczyzna zespolona
{z:Imz (z−1)≥0 }
{z: Imz (x+yi−1)≥0 }
{z: Imz (y−1)≥0}
y≥1
12 paź 18:10
Lidka:
Ma być: Im (z−1) ?
12 paź 18:21
Paulina:
tak Im (z−1)≥0
12 paź 18:24
Lidka:
Im(x+iy−1)=Im[(x−1)+iy)]=y
y≥0 (wszystko nad osią OX)
12 paź 18:27
Paulina:
z−1≥0
y≥1
przecież to jest obszar nad osią ?
12 paź 18:29
bezendu:
im(x+yi−1)≥0
y−1≥0 ⇒y≥1
I masz dobrze
12 paź 18:35
PW: Część urojona liczby z i liczby z−1 są takie same.
12 paź 18:35
Paulina:
Hmm czyli dobrze mam
12 paź 18:42
Janek191:
Nie ! :
Im ( x + yi − 1) = Im ( ( x − 1) + yi ) = y
y ≥ 0
To półpłaszczyzna nad osią OX z tą osią !
12 paź 18:45
Paulina:
przepraszam za kłopot
ale już zrozumiałam
!
12 paź 18:49
Lidka:
bezendu, źle.Czytaj 18:27 i to samo 18:45
12 paź 18:56
Lidka:
Dla przećwiczenia:
Im( (1+2i)*z−3i)<0
12 paź 18:58
Paulina:
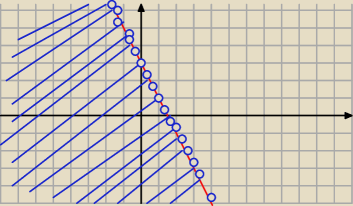
Im ( (1+2i)z−3i )<0
Im (z+2zi−3i)<0
Im (x+yi+2i(x+yi)−3i)<0
Im (x+yi+2xi−2y−3i) <0
y+2x−3<0
y<−2x+3
12 paź 19:12
Lidka:
Bardzo dobrze.
Trzeba jeszcze ładnie oddzielić część Re i część Im
Im( (x−2y)+(y+2x−3)*i)=y+2x−3
12 paź 19:21
Paulina:
Dziękuję, potem jeszcze będę mogła zająć chwilkę
?
Mam jeszcze troszkę przykładów a wiem, że każdy ma swoje sprawy i nie bardzo chcę zawracać
głowę bo w końcu to forum maturalne
12 paź 19:32
Lidka:
Pisz, zawsze ktoś pomoże, dużo studentów jest na forum.
12 paź 19:47
Paulina:
b) Re(z+i)2≥0⇔Re(z2+2zi+i2)⇔
Re(x2+2xyi−y2+2xi−2y−1)≥0⇔
Re[(x2−y2−2y−1)+(2xy+2x)i]≥0⇔
x2−y2−2y−1≥0⇔x2−(y+1)2≥0⇔
|x|−|y+1|≥0
Tak ?
12 paź 22:07
Mila:
Tak.
Narysuj.
12 paź 22:12
Paulina:
Jeśli dobrze pamiętam z LO to trzeba 4 przypadki
|x|≥|y+1|
A nie da się szybciej bez rozpatrywania
x≥0 i y≥−1
x≥0 i y<−1
x<0 y<−1
x<0 y≥−1
12 paź 22:20
Mila:
Zobacz podobny przypadek, masz tam dwa sposoby.
12 paź 22:22
12 paź 22:22
12 paź 22:23
Paulina:
z2=2Re(iz)
x2+2xy−y2=2Re(xi−y2)
Co z tym począć ?
12 paź 22:30
Blue: Dzięki Mila i przepraszam za wtrącanie się w czyiś wątek, już nie będę
12 paź 22:40
Mila:
(x+iy)2=2*Re(i*(x+iy))
x2+2xyi−y2=2*Re(xi−y)
x2+2xyi−y2=−2y⇔
2xy=0 i x2−y2=−2y
rozwiąż.
12 paź 22:40
Mila:
Blue, nic nie szkodzi.
Pytaj, gdy masz problem. Widziałam, że Ci pomagają to nie wtrącałam się.
12 paź 22:42
Paulina:
x2+2y−y2 z tym mam problem.
Dawno nie robiłam takich zadań i wyleciał to z głowy..
12 paź 22:50
Mila:
2xy=0 ⇔x=0 lub y=0
1)x=0 i x2−y2+2y=0⇔
−y2+2y=0⇔y(−2+y)=0⇔y=0 lub y=2
mamy dwie liczby
z=0+0*i czyli z=0
lub
z=0+2i czyli z=2i
2) y=0 i x2−y2+2y=0⇔
x=0
znowu mamy z=0
12 paź 22:55
Paulina:
A mogę prosić o rysunek ?
12 paź 22:58
Mila:
Do której wersji.
12 paź 23:03
Paulina:
do zadania 22:30
12 paź 23:08
Mila:
A masz takie polecenie?
12 paź 23:12
Mila:
(0,0)
(0,2) dwa punkty tylko.
12 paź 23:13
Paulina: Tak, polecenie do tych zadań to przedstaw na płaszczyźnie zespolonej
12 paź 23:14
Mila:
Tak, jak napisałam 23:13
12 paź 23:17
Paulina:
Dziękuję
12 paź 23:18
Mila:
Idź spać.
12 paź 23:19
Paulina:
jeszcze ponad 40 zdań mam do zrobienia na wtorek... na tą wejściówkę.
12 paź 23:26
Mila:
Jednak trzeba odpoczywać, aby mieć jasny umysł.
Dobranoc.
12 paź 23:31
Paulina:
Dobranoc..
12 paź 23:33