nierownosc Kris: |x| ≥ |y−1| Jak to narysować w układzie współrzędnych ?

Kris: Znalazlem jak to wyglada tylko nie wiem dlaczego tak

Kris: Znalazlem jakto wyglada tylko nie wiem dlaczego tak

sushi_gg6397228: jak sie robi zadania z wartością bezwzgledna ?

Kris: W tym przypadku chyba beda 4 przypadki

sushi_gg6397228: i bede 4 proste potem trzeba wybrac odpowiednie obszary i po zabawie

Kris: Ok sushi wyszlo pieknie dzieki

sushi_gg6397228: na zdrowie

pigor: ..., np. tak : |x| ≥ |y−1| ⇔ ⇔ |y−1| ≤ |x| ⇔ −|x| ≤ y−1 ≤ |x| /+1 ⇔ −|x|+1 ≤ y ≤ |x|+1 i rysuj w jednym układzie osi xOy wykresy y=−|x|+1 i y=|x|+1 i zaznacz odpowiedni na płaszczyźnie z xOy obszar (część wspólna − iloczyn) punktów (x,y) ; −−−−−−−−−−−−−−−−−−−−− lub x² ≥ (y−1)² ⇔ (y−1)²−x² ≥0 ⇔ (y−1−x)(y−1+x) ≥0 ⇔ ⇔ (y−1−x ≥0 i y−1+x ≥0) v ((y−1−x ≤0 i y−1+x ≤0) itd rysujesz proste : y=x+1 i y=−x+1 i masz zbiór (x,y) w układzie xOy. między nimi wraz z punktami na nich ...

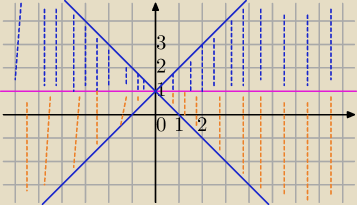
Mila: |y−1|=y−1 ⇔y−1≥0⇔y≥1 punkty nad prostą y=1 i na prostej 1) y−1≥0 |x|≥y−1⇔ |x|+1≥y y≤|x|+1 poniżej wykresu y=|x|+1 i nad prostą y=1 2) |y−1|=−y+1 dla y<1 |x|≥−y+1 i punkty pod prostą y=1 y≥−|x|+1 i na wykresem y=−|x|+1