Jak wyliczić współrzędne wierzchołka? MC: mam pytanko jesli mam 3 funkcje y>= (2/3)x − 3 y<=(−3/2)x + 3 x>= −1 z tych funkcji mam narysować trójkąt ale jak mając te wzory funkcji wyznaczyć współrzędne wierzchołka tego trójkąta?+ udowodnić z te trójkąt jest prostokątny i obliczyc pole koła opisanego na tym trójkącie

daras: wierzchołek=miejsce wspólne dla obu boków=> rozwiąż równania parami

daras:

	2		3		36		15
Pierwszy wierzchołek:		x − 3 = −		x + 3 => A (		; −		)
	3		2		13		13

	11
drugi: B( −1; −		)
	9

i trzeci: C( −1; 4,5) teraz narysuj Δ albo sprawdź wzorem (https://matematykaszkolna.pl/strona/1629.html ) kosinusy kąta między bokami (wektorami: AB BC i CA), jeśli wyjdzie ci 0 tzn., że kąt między nimi jest prosty.

	2		3
Możesz też porównać współczynniki kierunkowe prostych: https://matematykaszkolna.pl/strona/42.html widać, że −				= −1
	3		2

więc są prostopadłe, sposobów jest więcej i dla chcącego nic trudnego

daras:

	11
przy drugim wierzchołku powinno być : B(−1; −		)
	3

daras: 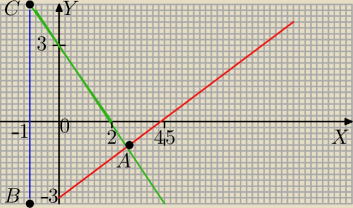3y − 2x + 9 = 0 2y + 3x − 6 = 0 x = −1 Wierzchołki wyznaczamy jako punkty przecięcia się prostych rozwiązując poniższe układy r−ń:

	⎧	3y − 2x + 9 = 0
A:	⎩	2y + 3x − 6 = 0

	⎧	3y − 2x + 9 = 0
B:	⎩	x = −1

	⎧	2y + 3x − 6 = 0
C:	⎩	x = −1

	36		15		11
dostaniemy: A(		; −		), B(−1; −		), C(−1; 4,5)
	13		13		3

Teraz sprawdzamy czy wektory AC^→ i AB^→ są prostopadłe

	36		15
AC→ = [ −1 −		; 4,5 +		]
	13		13

	36		11		15
AB→ = [−1 −		; −		+		]
	13		3		13

wyznaczamy ich iloczyn skalarny:

	36		9		15		15		11
AC→ ◯ AB→ = (1 +		)2 + (		+		)(		−		) =
	13		2		13		13		3

	49		147		−98
= (		)2 +		(		) = 0 co oznacza że cos∡(AC→;AB→) = 0 czyli
	13		26		39

∡(AC^→;AB^→) = 90^o

daras: Jeżeli Δ prostokątny jest wpisany w okrąg, to jego przeciwprostokątna jest średnicą tego okręgu S_o = 9π