Całka podwójna - obszar całkowania Piotrek12: Witam, myślałem że potrafię jednak nie potrafię. Może mi ktoś z dobrych duszyczek tu , dobrze wyjaśnić jak określić obszar całkowania? Chodzi o te że coś ≤ x≤ coś coś ≤ y≤ coś Z góry dzięki.

Ajtek: Granice całkowania to są

Piotrek12: Nie wiem jak to się fachowo nazywa ale to chyba to

Mila: Napisz zadanie.

Piotrek12: Nie mam żadnego. Może Wy macie jakiś prosty przykład na którym da się to wytłumaczyć.

bezendu: http://lmgtfy.com/?q=ca%C5%82ka+podw%C3%B3jna-jak+wyznaczy%C4%87+obszar+ca%C5%82kowania

Piotrek12: znalazłem jakieś w necie Oblicz całkę ∫∫xdxdy d: y=x² , y=2x

Piotrek12: Przepraszam że to napiszę, ale czy Pan myśli że tego nie wpisywałem? Aż tak tępy nie jestem, żeby od razu na forum lecieć. Tamte nie są dla mnie za jasno opisane, dlatego napisałem tu.

Mila: 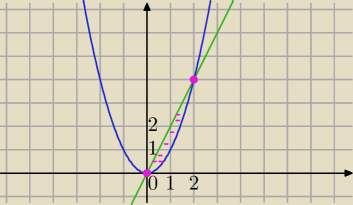y=x² y=2x Obszar normalny względem OX. Punkty przexcięcia x=0, x=2 stałe granice całkowania y=x², y=2x zmienne granice całkowania. Przepraszam, że pytam, na wykładach i ćwiczeniach było?

Piotrek12: Studia zaoczne, ćwiczenia z matmy 15 godzin niestety typ nie zdążył z materiałem i na egzaminie to wyrzucił. Wykłady 30 godzin, typ zdążył ale poświęcił na to 1 godzinę i na zaliczenie muszę mu zrobić to 1 zadanie xD Nie wiem czemu na zbieżność szeregu poświęcił 10 godzin i robił to do znudzenia a na coś trudniejszego tylko 1 godzinę i to na ostatnim wykładzie. W sumie to Ci wykładowcy robią co chcą...

Piotrek12: No dobrze, wykres narysowałem sobie sam na kartce i w sumie to tyle co umiem z tego zadania zrobić ... Tyle tylko że ja nadal nie mam pojęcia jak to rozpisać na coś takiego: coś ≤ x≤ coś coś ≤ y≤ coś Jak tego dobrze nie rozpiszę to potem źle to zcałkuję. Dalszą część zadania umiem zrobić tylko w tym momencie staje.

Mila: W Krysickim jest to dokładnie wyjaśnione na przykładach. To sam masz sobie wymyślać zadanie? Nic z tego nie rozumiem. 0∫1(x2 ∫2xx dy) dx= liczysz całkę po y ( x− traktujesz jak stałą) =0∫1 [x*y]x22x=0∫1 (x*(2x)−x*x2) dx= =0∫1(2x2−x3) dx spróbuj dokończyć.

Mila: 0≤x≤2 obszar w granicach: x zmienia się od 0 do 2 ( popraw w całkach 21:38) x²≤y≤2x zmienna y zmienia się od x² do 2x. Jeśli masz problem to pytaj.

Mila: Tu masz inny przykład. https://matematykaszkolna.pl/forum/256049.html

Piotrek12: obczajam to i coś mi chyba wychodzi, zrobiłem takie zadanie ∫∫xydxdy D:y=x² , y=x rysunek: http://www.wolframalpha.com/input/?i=y%3Dx^2%2C+y%3Dx Granice: 0≤x≤1 x²≤y≤x Wynik tego wyszedł mi 1/6 Jakby ktoś mógł czy taki wynik ma wyjść. Z góry dzięki.

Mila: Ja mam wynik:

	1
	24

Napisz swoje obliczenia.Granice masz dobrze.

Piotrek12: Nie ogarniam pisania w tym lateXie, wrzucę link do zdjęcia z zeszytu, mam na 100% źle, tylko nie wiem co http://zapodaj.net/27ab69294b483.jpg.html

Mila: Byłoby dobrze, gdyby nie jedno odejmowanie, 1)x⁵ i x³ to nie są wyrazy podobne− nie możesz zredukować. 2) odwrotnie granice x i x²− wykres y=x leży na wykresem y=x² w przedziale <0,1>, zatem x − granica górna, x² − granica dolna Zapisy też poprawimy. ₀∫¹[_x²∫^x(x)y dy]dx=

	1		1		1
=0∫1([		xy2]x2x) dx=0∫1[		x*(x)2−		x*(x2)2]dx=
	2		2		2

	1		1		1		1		1
=0∫1[		x3−		x5]dx=		[		x4−		x6]01=
	2		2		2		4		6

	1		1		1		1		3		2		1		1		1
=		[		−		−0+0]=		*(		−		)=		*		=
	2		4		6		2		12		12		2		12		24

Piotrek12: Boże dzięki! Biorę się za next przykład

Mila: Dobrze, pracuj solidnie.

Piotrek12: Zrobiłem bardzo podobny przykład. Proszę o sprawdzenie. ∫∫xydxdy D:y=x, y=0 , x=1 Rysunek, nie chce mi się wygenerować ale w zeszycie wychodzi połowa kwadratu granice 0≤x≤1 0≤y≤1 Wynik: 1/2 Link do zadania: http://zapodaj.net/497e42c3043ba.jpg.html

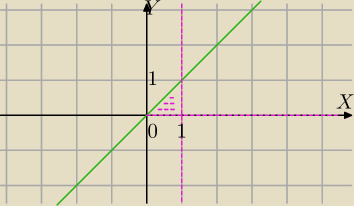
Mila: Masz obszar ograniczony prostą y=x, prostą x=1 i prostą y=0 0≤x≤1 0≤y≤x

	1
0∫1[0∫x(xy)dy]dx= teraz licz wynik
	8

Piotrek12: Okeeey Poprawiłem

Mila:

Piotrek12: A jaka tu będzie granica? ∫∫ydxdy y=1−x², y=x+1 według mnie: −1≤x≤1 1−x²≤y≤x+1 ale chyba jest źle bo mi chore wyniki wychodzą

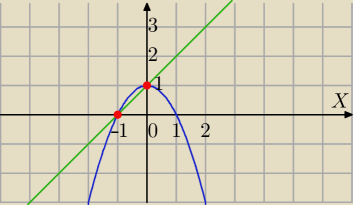
Mila: 1−x²=x+1⇔x²+x=0⇔ x(x+1)=0 x=0 lub x=−1 −1≤x≤0 x+1≤y≤1−x² Teraz zapisz całki i licz. Napisz wynik, albo przeslij zdjęcie rozwiazania.

Piotrek12: wynik mi wyszedł − 1/2 xDD pewnie źle

Mila:

1
10

pokaż rozwiązanie. Coś trzeba poprawić.

Piotrek12: Popróbuje sam metodą prób i błędów, jak się nie uda to wtedy wrzucę,

Piotrek12: Jednak sobie nie poradzę, ciągle wychodzi mi coś innego ... Jestem za durny na tą całkę... http://zapodaj.net/46e9d12d870ef.jpg.html Dzięki Ci jeszcze raz za to że mi tak pomagasz..

Mila: Oj, nie czytasz uważnie tego, co Ci napisałam. 17:18 ₋₁∫⁰ [_x+1∫^1−x2 (y)dy]dx= obszar od prostej do góry do paraboli, dla x∊<−1,0 > Teraz licz, jak nie wyjdzie, to napiszę, ale musisz to pojąć, to proste.

Piotrek12: Nie no nie wierzę znowu źle.... brak słów .....

Mila:

	1
...=−1∫0([		y2]x+11−x2)dx=
	2

	1		1
=−1∫0		[(1−x2)2−(x+1)2] dx=		−1∫0(1−2x2+x4−x2−2x−1) dx=
	2		2

	1		1		1
=		−1∫0(x4−3x2−2x) dx=		[		x5−x3−x2]−10=
	2		2		5

	1		1		1		−1		−1		1
=		*0−		*(−		+1−1)=		*		=
	2		2		5		2		5		10

Piotrek12: Jesteś mega! dzięki po raz kolejny. A jaki wynik ma wyjść w ∫∫xdxdy D: y=x² i y=2−x Wczoraj to zrobiłem I wyszedł mi 3 i 3/4 pewnie źle

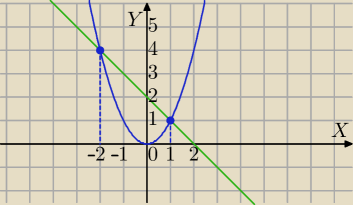
Mila: −2≤x≤1 x²≤y≤2−x

	9
−2∫1[y=x2∫y=2−x(x)dy]dx=−
	4

Piotrek12: ja nie wierzę... jestem jakiś turbo tępy robię ten przykład po raz 24 i za każdym razem mam co innego xDDD i ani razu wynik nie był poprawny....

Mila: −2∫1([xy]x22−x) dx= teraz spokojnie dalej licz, pomyłki zdarzają się, ja też liczyłam 3 razy.

Patryk: Mila prosze pomóż https://matematykaszkolna.pl/forum/256668.html błagam wręcz

Mila: cd=₋₂∫¹(x*(2−x)−x*x²) dx=

	1		1		1
=−2∫1(2x−x2−x3)dx=[2*		x2−		x3−		x4]−21=
	2		3		4

	1		1
=[x2−		x3−		x4]−21=
	3		4

	1		1		1		1
=1−		−		−(4−		*(−8)−		*16)=
	3		4		3		4

	4		3		8		7		32		39		13		9
=1−		−		−		=1−		−		=1−		=1−		=−
	12		12		3		12		12		12		4		4

Teraz powiedz, co źle robiłeś.

Piotrek12: 1 wiersz mam dobrze 2 wiersz mam dobrze 3 wiersz mam dobrze 4 wiersz nie wiem czemu jest *(−8) skoro −2² nie daje −8 5 wiersz mam źle bo nie mam tej 8.

Mila:

	1		1
−		x3=−		*(−2)*(−2)*(−2) tam masz trzecia potęgę.
	3		3

Piotrek12: i wszystko jasne... xD

Mila: Dobranoc

Piotrek12: Ok, dzięki Mila! Idę spać,jutro od rana znów cisne całki, mam nadzieję że masz jeszcze cierpliwość mi pomagać. Jeszcze raz dziękuje i dobranoc

Mila:

Piotrek12: Mila przerobiłem sobie dziś na spokojnie te wszystkie zadania co tu robiliśmy i wyszło mi dobrze. Masz może jakieś przykłady, bo mi się już skończyły

Piotrek12: Może do niedzieli to ogarnę żeby zaliczyć xDD

Piotrek12: Mam jeszcze jedno. ∫∫xdxdy D: x=0, y=0, 3x+2y=6 Jaki tu obszar będzie?

Mila: Wyznacz y z równania prostej , znajdź miejsce zerowe.x₀ 0≤x≤x₀

	−3
0≤y≤		x+3
	2

Piotrek12: Ok, to zrobię zaraz, ale zaczałem robić inny przykład i mi nie wychodzi. ∫∫xdxdy D: x², y²=x Granice: 0≤x≤1 x²≤y≤√x Coś mam źle bo wychodzi mi ta 1 całka x³−(x*√x)

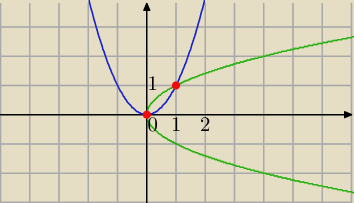
Mila: Granice w porządku ( widzę, że jest postęp) y=x² y²=x y=√x dla x≥0 lub y=−√x dla x≥0 0≤x≤1 x²≤y≤√x ₀∫¹[_x²∫^√x (x)dy]dx=₀∫¹(x√x−x³) dx= [Przekształcam: x*x^1₂=x^3₂ ]

	2		1		3
=0∫1(x32−x3)dx=[		x52−		x4]01=
	5		4		20

Piotrek12: ∫∫xdxdy D: x=0, y=0, 3x+2y=6 równanie prostej: y=−1/1/2x+3 Granice: 0≤x≤2 0≤y≤−1/1/2x+3 wynik: 10 Pewnie źle xD

Mila: Licz jeszcze raz . =2

Piotrek12: Boże tak mam 2 xD zamiast −4 +6 dałem 4+6 ...

Mila: To drobny błąd rachunkowy, miałbyś całkę zaliczoną, o ile w środku masz porządne zapisy.

Piotrek12: Masz może jakiś przykład? Porobię jeszcze przed pracą coś

Mila: W tej chwili nie i nie bardzo mam czas, wpadłam na chwilę, będę po 21 miałam czas. Nie martw się już masz lepszą orientację.

Piotrek12: Ja będę dopiero po 24 poszukam w necie może coś znajdę Dzięki wielkie!

Mila: http://katmat.pb.bialystok.pl/~wyrwas/bud2_zaoczni/cw_calki_podwojne.pdf

Piotrek12: Dzięki idę robić

Mila: Załóż nowy wątek, bo długo trzeba przwijać.

xD: Mila Trzymaj jutro kciuki od 13−15 xD

xD: Mila Trzymaj jutro kciuki od 13−15 xD

xD: Zaliczone!

Mila: Piotrek to Ty? Naprawdę całki zaliczone.

Piotrek12: Tak, zaliczone i nawet innym pomagałem miałem mini błąd więc 3+ a nie 4, ale ważne że zaliczone.

Piotrek12: Dzięki Ci wielkie!