Całka podwójna ratunku Piotrek12: Obliczyć całkę ∬ydxdy gdzie D: y=1−x² , y=x+1 Rysunek: http://www.wolframalpha.com/input/?i=y%3D1-x^2%2C+y%3Dx%2B1 Dalej nie bardzo wiem, jak się za to zabrać, proszę o wytłumaczenie. Z góry dziękuje!

Piotrek12: Pomoże ktoś?

Kacper: Rysunek masz?

Piotrek12: Dałem przecież w linku

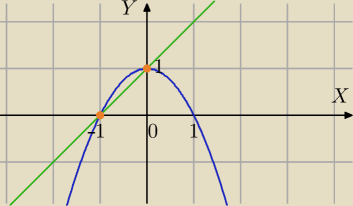
Mila: Punkty przecięcia : (−1,0),(0,0) ₋₁∫⁰_y=x+1∫^y=1−x2(1) dy dx= =₋₁∫⁰([y]_y=x+1^y=1−x2)dx=

	−1		1
=−1∫0(1−x2−x−1)dx=−1∫0(−x2−x)dx=[		x3−		x2]−10=
	3		2

	−1		1		1
=		+		=
	3		2		6

Mila: Przepraszam. Poprawiam, bo nie zauważyłam (y) pod całką. {−1}∫⁰_y=x+1∫^y=1−x2(y) dy dx=

	1
=−1∫0(		y2|y=x+1y=1−x2})dx=
	2

	1
=		*−1∫0((1−x2)2−(1+x)2)dx=
	2

	1		1		1
=		*−1∫0(x4−3x2−2x)dx=		[		x5−x3−x2]−10=
	2		2		5

	1		−1		1
=−		*(		+1−1}=
	2		5		10

Piotrek12: Ok dzięki, wszystko kumam, tylko nie bardzo tego co jest na górze a co na dole przy znaku ∫.

Mila: To są granice całkowania ; Przeczytaj w książce, najpierw zmienne granice , potem stałe. Zmienne granice : dolna y=x+1, górna y=1−x². stałe : x=−1 dolna granica , x=0 − górna granica

Mila: W Krysickim jest pięknie wytłumaczone.

Piotrek12: Ok! Dzięki Już wiem

Mila: