Geom Lukas: A#8 Dla jakich wartości parametru m równanie x² + y²−2mx + 2m − 1 = 0 opisuje okrąg? c) Dla jakich wartości parametru m okrąg ten jest styczny do prostej o równaniu x = 4 ? (x−m)²−m²+y²+2m−1=0 (x−m)²+y²=m²−2m+1 (x−m)²+y²=(m+1)² (x−m)²+y²=|m+1| |m+1|=4 m+1=4 lub m+1=−4 m=3 m=−5 ok ?

wmboczek: |m−4|=m+1 w drugiej części

Eta: Sprawdź swoje obliczenia ? a)S(m,0) , r=|m−1| ⇒m∊R\{1}

	1
b) |m−4|=|m−1| ⇒ .......... m=2
	2

Lukas: Faktycznie r=|m−1| tylko skąd Ty masz a) i b) jak ja podałem tylko c) ? 2. Może ktoś wytłumaczy skąd |m−4|=|m−1| a nie tylko dokończ ?

Eta: Znów się "czepiasz" odp 1/ ...... odp 2/ ......

Saizou : odległość prostej od środka okręgu jest równa promieniowi, wtedy prosta ma jeden punkt wspólny z okręgiem xd

Eta:

Saizou :

Eta: |m−4|=|m−1| ⇔ m−4=m−1 lub m−4= −m+1 ⇒ .........................

Lukas: Czepiam się bo to wygląda tak ja by ktoś rozwiązał za mnie całe zadanie a mi kazał wpisać tylko wyniki... Pisałem, że nie chcę się tak uczyć Więc jakiś komentarz skąd się to bierze to by się przydał. Dziękuję....

Lukas: odległość prostej od środka okręgu jest równa promieniowi to |m−1|=4 środek =|m−1| prosta x=4

Saizou : prosta w postaci x−4=0 S(m:0) d=..... https://matematykaszkolna.pl/strona/1249.html

Lukas: Ok teraz już zrozumiałem.

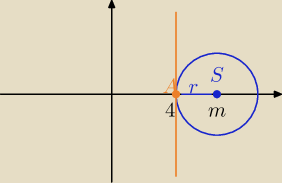
Eta: |SA|=√(m−4)²+0=|m−4| , r= |m−1|

Lukas: Dziękuję

Eta:

Lukas: Są jeszcze jakieś takie własności jak o tej odległości prostej od środka okręgu ?

5-latek: Lukas ale to ze zwyklej geometrii powinienes wiedziec ze styczna do okregu ma jeden punkt wspolny z okregiem i jest prostopadla do promienia

Lukas: Jeszcze zwykłej geometrii nie powtarzałem... Uzupełniam braki..

5-latek: takze powinienes wiedziec ze rownanie postaci x²+y²+ax+_by+c opisuje okrag jesli a²+b²−4c>0

5-latek: tam powinno byc rownanie x²+y²+ax+by+c=0

Lukas: a coś bardziej praktycznego ?

5-latek: np co chcialbys wiedziec ?

Lukas: Coś o stycznych do okręgu ?

Eta: https://matematykaszkolna.pl/strona/467.html

Eta: https://matematykaszkolna.pl/strona/466.html

Lukas: To wiedziałem a skąd się wzięło to 21:14 ?

Eta: 21: 14 ? nie wiem o co pytasz?

5-latek: To bardzo proszse Styczna do okregu (x−x_sr)²+(y−y_sr)²=r² w punkcie A(x₁,y₁) ma rownanie (x₁−x_sr)(x−x_sr)+(y₁−y_sr)(y−y_sr)=r²

Lukas: ''odległość prostej od środka okręgu jest równa promieniowi, wtedy prosta ma jeden punkt wspólny z okręgiem''

Eta: https://matematykaszkolna.pl/strona/466.html trzeci przypadek

Lukas: ok zapamiętam

Bogdan: Do 5−latka − co oznacza x_sr i y_sr w nawiasach?

5-latek: Witaj wspolrzedna x_owa srodka okregu i to samo wspolrzedna y_owa srodka okregu

Bogdan: Ale co oznacza r przy x_s?, z takim zapisem nie spotkałem się, zapis x_sr oznacza x_s * r. Raczej stosuje się takie zapisy: Równanie okręgu o środku S(x₀, y₀) i promieniu długości r: (x − x₀)² + (y − y₀)² = r² Równanie stycznej do okręgu w Punkcie A(x_A, y_A) należącym do tego okręgu: (x_A − x₀)(x − X₀) + (y_A − y₀)(y − y₀) = r²

5-latek: na klawiaturze jak piszesz x_sr to tak wyjdzie Oczywiscie mozna tez napisac (x₁−a)(x−a)+(y₁−b)(y₁−b)=r² gdzie a i b to wspolrzedne srodka okregu

Bogdan: a może chodziło Ci o zapis x_sr i y_sr ?