Błagam pomocy! Makówka: Dany jest trójkąt rozwartokątny równoramienny, którego boki mają długość 16 cm, 10 cm, 10 cm. Wyaznacz promień okręgu wpisanego w ten trojkąt oraz promień okręgu opsanego na tym trójkącie.

Lukas: wzory znasz ? to co za problem ?

5-latek: https://matematykaszkolna.pl/strona/541.html https://matematykaszkolna.pl/strona/542.html

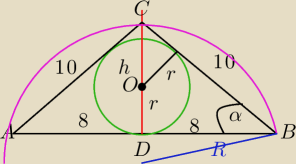
Mila: 1) h²+8²=10² h²=36 h=6

	h
sinα=
	BC

	6
sinα=
	10

Z tw. sinusów :

AC
	=2R
sinα

10
	=2R
0,6

	5		50		25
R=		=		=
	0,6		6		3

	25
R=		− dł. promienia okręgu opisanego na ΔABC
	3

========================================= 2) P_Δ=p*r, gdzie p− połowa obwodu Δ, r− promień okręgu wpisanego w Δ

	1
PΔ=		*|AB|*h
	2

	1
PΔ=		*16*6=48
	2

	10+10+16		36
p=		=		=18
	2		2

48=18*r

	48		8
r=		=
	18		3

	8
r=
	3

=========

Eta: Można tak:

	abc		10*10*16		25
R=		=		= ....... =
	4P		4*48		3