war
Lukas:
Ma ktoś link gdzie dobrze wytłumaczone są równania z wartością bez ?
30 maj 16:44
30 maj 16:59
30 maj 16:59
Lukas: dzięki
30 maj 17:08
Lukas:
Ale tam nie ma takich przykładów |x
2−9|+|x
2−16|=6 np i bardziej rozbudowanych

30 maj 20:34
30 maj 20:45
Lukas:
Te są proste bo trójmian jest tylko w jednym module a ja szukam takich jak podałem wyżej i z
wyjaśnieniem
30 maj 20:52
krystek:
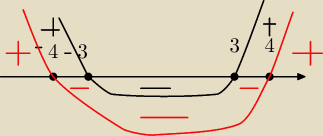
m zerowe to −4,−3,3,4 i rozpisujesz
30 maj 21:38
Lukas:
Ale w jednym z przedziałów wchodzi mi raz ujemne raz dodatnie

30 maj 21:39
krystek: Nie ,
30 maj 21:41
krystek: Np x∊<−4,−3) masz x2−9 −(x2−16)=6
30 maj 21:43
Lukas:
Wrzucam przykład z wczoraj bo tam nadal nic nie rozumiem
|x2−4|+|x+2|=6
1.(−∞,−2)
2.<−2,2)
3.<2,∞)
w drugim przedziale wychodzi mi raz
x2−4+x+2=6
a raz −x2+4+x+2=6
30 maj 21:44
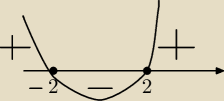
krystek: Nie może !
−(x2−4)+(x+2)=6
30 maj 21:49
krystek:
30 maj 21:51
Lukas:
Jak biorę −2 to jest ok ale jak 0 to już nie a to powinno w całym przedziale <−2,2) przyjmować
wartości ujemne

30 maj 21:54
krystek: Pomyśl
30 maj 21:58
Lukas:
Właśnie myślę i dojść do rozwiązania nie mogę

Inne przykłady bez problemu robię a tego
ruszyć nie mogę.
30 maj 22:02
Marcin:
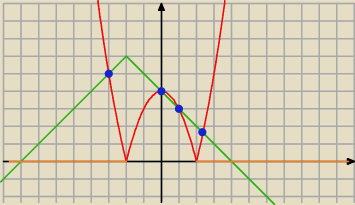
|x
2−4|+|x+2|=6 → |x
2−4|=6−|x+2|
Z rysunku widać 3 rozwiązania. Teraz jeszcze policz dla przedziału (2;
∞) i będziesz mieć
wszystko.
30 maj 22:12
kyrtap: Marcin ty rozwiązujesz graficznie ?
30 maj 22:13
WueR:
Powtorka z wczoraj, jak widze...
Tylko nie to.

30 maj 22:13
Marcin: Tak, graficznie

30 maj 22:14
kyrtap: Ok

30 maj 22:15
krystek: I(x+2)(x−2)I+Ix+2I=6
Ix+2I(Ix−2I+1)=6 też tak możesz
30 maj 22:16
Mila:
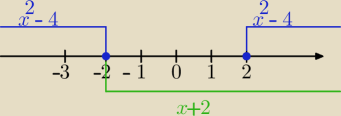
|x
2−4|+|x+2|=6
Z definicji wartości bewzględnej:
|x
2−4|=x
2−4 ⇔x
2−4≥0⇔x<−2 lub x>2
|x+2|=x+2⇔x+2≥0⇔x≥−2
Zaznaczam na osi gdzie wyrażenia są dodatnie i nie trzeba zmieniać znaku.
1) x≤−2
x
2−4+(−x−2)=6
x
2−x−12=0
Δ=49
itd
2) x∊(−2,2)
−x
2+4+x+2=6
−x
2+x=0
........
3)x≥2
x
2−4+x+2=6
x
2+x−8=0
..............
30 maj 22:18
kyrtap: Tak mi się podoba Mila

30 maj 22:19
30 maj 22:21
Mila:
Zobaczymy , co powie Łukasz?

30 maj 22:21
Lukas:
WueR Twoje żarty nie są śmieszne, Nie chcesz nie pomagaj a komentarze zostaw do siebie...
To jak mam |x2−16|+|x−8|=8
1. (−∞,−4)
2.<−4,8)
3.<8,∞)
2. dla =−4
x2−16
a dla −3∊<−4,8)
mam już −x2+16
z czego to wynika ?
30 maj 22:22
kyrtap: Marcin twoje też dobre, bardzo błyskotliwe rozwiązanie

30 maj 22:23
ZKS:
Pewnie z tego, że dla x = −3 masz wartość ujemną? Czy tak trudno rozwiązać jest nierówność
kiedy x2 − 16 ≥ 0 oraz x2 − 16 < 0 i pozaznaczać sobie to na osi tak jak pokazała Mila?
30 maj 22:26
Marcin:
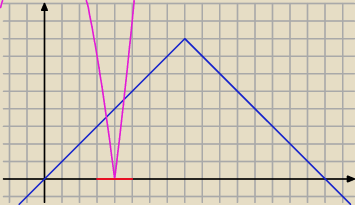
|x
2−16|+|x−8|=8 → |x
2−16|=8−|x−8|
Rozwiązania szukaj w przedziale (3;5)
30 maj 22:27
Lukas:
Napisałem wyżej przedziały, więc nie wiem o co Ci chodzi ZKS

30 maj 22:29
Mila:
Miało być :
Z definicji wartości bewzględnej:
|x2−4|=x2−4 ⇔x2−4≥0⇔x≤−2 lub x≥2
dalej rozpisuję dokładniej:
|x2−4|=−x2+4 dla x∊(−2,2)
Nie wiem, po co ty podstawiasz jakies wartości i badasz znak?
30 maj 22:55
Lukas:
Żeby sprawdzić czy mam ujemną czy dodatnią wartość w module ?
30 maj 23:00
Blue: A mi by się przydała strona z dobrze wytłumaczonym rachunkiem różniczkowym dla liceum

30 maj 23:09
Lukas:
To załóż nowy tema, a nie tutaj robisz spam. Tutaj jest wartość bez
30 maj 23:10
Marcin: |x
2−16|+|x−8|=8
Skoro sam podałeś przedziały i nie wiesz jak zmieniać znaki, to podstaw jakąś liczbę z tego
przedziału. Jeżeli po podstawieniu masz liczbę dodatnią, to nie zmieniasz znaku wartości bez,
a jeżeli masz ujemną, to zmieniasz. Tyle

30 maj 23:14
kyrtap: Lukas naucz się mojej siatki znaków

30 maj 23:16
kyrtap: nie będziesz musiał już potem podstawiać

30 maj 23:17
Mila:
Lukas popatrz na oś, zaznaczyłam 22:18, gdzie nie zmieniasz znaku, to jest z definicji wartości
bezwzględnej,
w pozostałych przedziałach zmieniasz znak.
Wczytaj się w to co napisałam. Wszyscy moi uczniowie tak rozwiązują i nie mają problemu z
wartością bewzględną.
30 maj 23:24
Lukas:
czyli 21:44 źle są przedziały ?
30 maj 23:35
Mila:
Lukas, niektórzy tak piszą jak Ty zapisałeś, jest różnica w domknięciach.
Mnie uczyli, że domykamy tam gdzie |..|≥0, ale w granicznych punktach jest wartość 0, więc może
byc tak jak napisałeś.
np. |x2−4|=|−x2+4|=0
x=−2 lub x=2
30 maj 23:41
kyrtap: Mnie uczyli Mila że domknięcia są tam gdzie więcej plusików

30 maj 23:44
Mila:
Ach, to chałupnictwo, co to znaczy więcej plusików, na przykładzie 22:18
Gdzie tam więcej plusików?
Naucz mnie tego sposobu.
30 maj 23:58
kyrtap: Na którym przykładzie ?
30 maj 23:58
Mila:
22:18
30 maj 23:59
kyrtap:
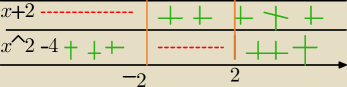
|x
2−4|+|x+2|=6
x
2 − 4 = 0 x= −2
x
2 = 4
x = −2 , x =2
Zaznaczam teraz to na siatce

31 maj 00:06
kyrtap: I potem sobie tworzę przedziały i widzę kiedy mam wyrażenie zmienić na przeciwne

31 maj 00:06
kyrtap: Jak oceniasz sposób ?

31 maj 00:07
Marcin: Też tak kiedyś robiłem

31 maj 00:09
kyrtap: Marcin i się nie spodobał chyba Tobie bo robisz graficznie

31 maj 00:10
Marcin: No ja sobie graficznie zawsze ogarniam, żeby mniej więcej zobaczyć w jakich przedziałach
spodziewać się rozwiązań

31 maj 00:12
Hajtowy: Marcinie wszystkiego można się spodziewać w każdym zadaniu

Też lubię graficzne rozwiązania


31 maj 00:16
pigor: ..., Rozwiąż równanie
|x2−4|+|x+2|=6 .
−−−−−−−−−−−−−−−−−−−−−
dyskusja o przedziałach jest co najmniej śmieszna, no to ja zrobię np. tak:
..., otóż przez podstawienie stwierdzam, że x=±2 nie spełniają danego równania,
więc szukam pierwiastków danego równania dalej
|x2−4|+|x+2|=6 ⇔
⇔ (x<−2 i x
2−4−x−2=6) v (−2<x<2 i −x
2+4+x+2=6) v (x>2 i x
2−4+x+2=6) ⇔
⇔ (x<−2 i x
2−x−12=0) v (−2<x<2 i x
2−x=0) v (x>2 i x
2+x−8=0) ⇔
⇔ (x<−2 i (x+3)(x−4)=0) v (−2<x<2 i x(x−1)=0) v (x>2 i x
2+x−8=0 i
√Δ=
√33) ⇔
⇔ x= −3 v x=0]] v x=1 v (x>2 i x
2+x−8=0 x
12(−1±
√33)) ⇔
⇔
x= −3 v
x=0 v
x=1 v
x=12(−1+√33, czyli
x∊{−3,0,1,−1+√33} − szukany
zbiór rozwiązań danego równania . ...

31 maj 00:19
Lukas:
Dziękuję, najbardziej podoba mi się sposób Mili

31 maj 01:36
Lukas:
Chyba mój błąd polega na złym zapisie przedziału <−2,2) nie może być ale (−2,2) już pasuje.
31 maj 16:09
Mila:
Teraz bojowa próba:
Określ liczbę rozwiązań równania w zależności od prametru m.
|x2−6x+8|+|x2−6x+5|=m
Przekopiuj do nowego wątka.
31 maj 16:20

 m zerowe to −4,−3,3,4 i rozpisujesz
m zerowe to −4,−3,3,4 i rozpisujesz



 Inne przykłady bez problemu robię a tego
ruszyć nie mogę.
Inne przykłady bez problemu robię a tego
ruszyć nie mogę.
 |x2−4|+|x+2|=6 → |x2−4|=6−|x+2|
Z rysunku widać 3 rozwiązania. Teraz jeszcze policz dla przedziału (2;∞) i będziesz mieć
wszystko.
|x2−4|+|x+2|=6 → |x2−4|=6−|x+2|
Z rysunku widać 3 rozwiązania. Teraz jeszcze policz dla przedziału (2;∞) i będziesz mieć
wszystko.



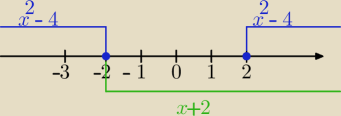 |x2−4|+|x+2|=6
Z definicji wartości bewzględnej:
|x2−4|=x2−4 ⇔x2−4≥0⇔x<−2 lub x>2
|x+2|=x+2⇔x+2≥0⇔x≥−2
Zaznaczam na osi gdzie wyrażenia są dodatnie i nie trzeba zmieniać znaku.
1) x≤−2
x2−4+(−x−2)=6
x2−x−12=0
Δ=49
itd
2) x∊(−2,2)
−x2+4+x+2=6
−x2+x=0
........
3)x≥2
x2−4+x+2=6
x2+x−8=0
..............
|x2−4|+|x+2|=6
Z definicji wartości bewzględnej:
|x2−4|=x2−4 ⇔x2−4≥0⇔x<−2 lub x>2
|x+2|=x+2⇔x+2≥0⇔x≥−2
Zaznaczam na osi gdzie wyrażenia są dodatnie i nie trzeba zmieniać znaku.
1) x≤−2
x2−4+(−x−2)=6
x2−x−12=0
Δ=49
itd
2) x∊(−2,2)
−x2+4+x+2=6
−x2+x=0
........
3)x≥2
x2−4+x+2=6
x2+x−8=0
..............

 http://goo.gl/KyVYFr
http://goo.gl/KyVYFr


 |x2−16|+|x−8|=8 → |x2−16|=8−|x−8|
Rozwiązania szukaj w przedziale (3;5)
|x2−16|+|x−8|=8 → |x2−16|=8−|x−8|
Rozwiązania szukaj w przedziale (3;5)






 |x2−4|+|x+2|=6
x2 − 4 = 0 x= −2
x2 = 4
x = −2 , x =2
Zaznaczam teraz to na siatce
|x2−4|+|x+2|=6
x2 − 4 = 0 x= −2
x2 = 4
x = −2 , x =2
Zaznaczam teraz to na siatce 





 Też lubię graficzne rozwiązania
Też lubię graficzne rozwiązania 


