sinusy/cosinusy
nicaled: Wykaż, że jeśli w trójkącie o kątach α, β, γ zachodzi związek sinα/ 2sinβ= cosγ,
to ten trójkąt jest równoramienny.
29 maj 16:50
nicaled: błagam o pomoc!
29 maj 18:45
Godzio:
Na przykład tak:
Z twierdzenia sinusów:
| a | | b | | sinα | | a | |
| = |
| ⇒ |
| = |
| |
| sinα | | sinβ | | sinβ | | b | |
Z twierdzenia cosinusów:
| | a2 + b2 − c2 | |
c2 = a2 + b2 − 2abcosγ ⇒ cosγ = |
| |
| | 2ab | |
a
2 + b
2 − c
2 = a
2
b
2 = c
2 ⇔ b = c
29 maj 18:51
nicaled: tylko, że ja mam wykazać, że a=b. jak byłbyś miły to narysuj rysunek do Twoich obliczeń

29 maj 18:55
Godzio:
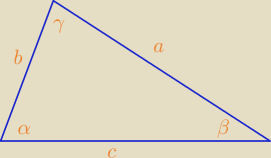
29 maj 18:57
nicaled: mam identyczny, dlatego chodzi mi o wykazanie, że a =b a nie, że c=b
29 maj 18:58
Godzio:
Ja Ci rozwiązania niepoprawnego nie wyczaruje

(zadanie jest zrobione poprawnie, nie wiem
gdzie masz problem)
29 maj 18:59
nicaled: po prostu nie za bardzo to rozumiem

29 maj 19:00
Godzio:
Czego?
29 maj 19:00
kyrtap: Może nie znasz wzorów i dlatego poczytaj sobie o tw. sinusów i cosinusów
29 maj 19:01
nicaled: no, bo udowodniłeś, że podstawa jest równa bokowi. a z treści wynika, że boki mają być sobie
równe.
29 maj 19:01
kyrtap: trzymaj mnie Godzio

29 maj 19:03
Godzio:
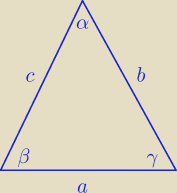
Rysunek sobie rysujesz jak chcesz, masz pokazać równość dwóch dowolnych boków, tutaj wyszło, że
b = c i nic tego nie zmieni.
Taki rysunek Ci pasuje?
29 maj 19:03
29 maj 19:05
Eta:
Można też tak:
W każdym trójkącie α+β+γ=180o ⇒ α= 180o−(β+γ)
sinα= sin[180o−(β+γ)= sin(β+γ) = sinβ*cosγ+sinγ*cosβ
to równość
sinα=2sinβ*cosγ
sinβ*cosγ+sinγ*cosβ= 2sinβ*cosγ
sinγ*cosβ−sinβ*cosγ=0
sin(γ−β)=0 ⇒ γ=β −−−zatem trójkąt jest równoramienny
c.n.w
29 maj 19:06
pigor: ..., wykaż, że jeśli w trójkącie o kątach α,β,γ zachodzi
związek
sinα2sinβ =cosγ, to ten trójkąt jest równoramienny.
−−−−−−−−−−−−−−−−−−−−−−
np. tak :
z wzorów tablicowych na sinus sumy lub różnicy dwóch kątów:
sinα2sinβ =cosγ /*2sinβ≠0 ⇒ sinα= 2sinβcosγ i α+β+γ=180
o ⇒
⇒ sin[(180
o−(β+γ)]= 2sinβcosγ ⇔ sin(β+γ)= 2sinβcosγ ⇔
⇔ sinβcosγ+sinγcosβ −2sinβcosγ= 0 ⇔ sinγcosβ−sinβcosγ= 0 ⇔
⇔ sin(γ−β)= 0 ⇔
y−β=0o ⇔
β=γ, czyli to c.n.w. . ...

29 maj 19:15
pigor: ...ups

naprawdę nie wiedziałem, że już jest rozwiązanie. ...

29 maj 19:16
Eta:

29 maj 19:18
pigor: ... nie wiem jak Wy potraficie tak szybko to wszystko napisać

bo ja piszą online i nigdy nie wiem co mi wyjdzie , stąd tyle to trwa ...
a jak bym widział zwłaszcza wymagania a= b

" autorki postu na pewno
bym się nie męczył .
29 maj 19:27
Eta:
@
π..r...jedz więcej


dobrze działa na przyśpieszony "zapłon"

29 maj 19:33
Kacper:
biorę

24 sty 21:23


 (zadanie jest zrobione poprawnie, nie wiem
gdzie masz problem)
(zadanie jest zrobione poprawnie, nie wiem
gdzie masz problem)


 Rysunek sobie rysujesz jak chcesz, masz pokazać równość dwóch dowolnych boków, tutaj wyszło, że
b = c i nic tego nie zmieni.
Taki rysunek Ci pasuje?
Rysunek sobie rysujesz jak chcesz, masz pokazać równość dwóch dowolnych boków, tutaj wyszło, że
b = c i nic tego nie zmieni.
Taki rysunek Ci pasuje?
 https://matematykaszkolna.pl/forum/251924.html
https://matematykaszkolna.pl/forum/251923.html
moglibyście pomyśleć też nad tym?
https://matematykaszkolna.pl/forum/251924.html
https://matematykaszkolna.pl/forum/251923.html
moglibyście pomyśleć też nad tym? 

 naprawdę nie wiedziałem, że już jest rozwiązanie. ...
naprawdę nie wiedziałem, że już jest rozwiązanie. ...

 bo ja piszą online i nigdy nie wiem co mi wyjdzie , stąd tyle to trwa ...
a jak bym widział zwłaszcza wymagania a= b
bo ja piszą online i nigdy nie wiem co mi wyjdzie , stąd tyle to trwa ...
a jak bym widział zwłaszcza wymagania a= b  " autorki postu na pewno
bym się nie męczył .
" autorki postu na pewno
bym się nie męczył .

 dobrze działa na przyśpieszony "zapłon"
dobrze działa na przyśpieszony "zapłon" 
