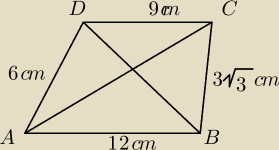
planimetria nicaled: 1.Oblicz długość przekątnej AC czworokąta ABCD przedstawionego na rysunku, jeśli przekątna BD ma długość 6√3 cm.

nicaled: błagam o pomoc!

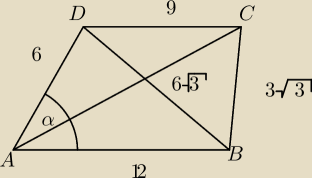
kyrtap: Zastosuj tw. cosinusów dla Δ ABD aby obliczyć kąt alfa

kyrtap: jak wyliczysz daj znać

nicaled: przekątna to x. wyszło mi, że 12²=6²+x²−2*6*x*cosα 112=x²−12xcosα

kyrtap: poczytaj o tw. cosinusów jak się je definiuje bo źle zapisałaś/eś

kyrtap: IBDI² = IADI² + IABI² − 2IABI IADI cosα

nicaled: x²=180−144 cosγ ?

nicaled: tak zrobiłem

kyrtap: przecież w trójkącie ABD masz wszystkie boki podane i masz wyliczyć alfę więc gdzie ty masz tam niewiadomą x ?!

nicaled: przecież przekątną to ja mam wyliczyć. więc skąd jest to 6√3

kyrtap: a masz podaną miarę kąta ADC ? chyba nie co?

nicaled: a sorry! nie zauważyłem tego co jest w danych. przepraszam

nicaled: mam. α=30st

kyrtap:

	1
cosα =		to na pewno 30 st.?
	2

nicaled: no tam jest 60, ale Ty chciałeś 1/2 tego, tak? przynajmniej tak wynika z rysunku

kyrtap: nie chciałem całą alfę

nicaled: czyli 60st

nicaled: a co z tym dalej?

jsjsj: mozna to prosto obliczyć z tw.Pitagorasa. bo udowodniłem ze trójkąt jest prostokatny (Abc)